1. 引言
双列圆锥滚子轴承外圈或内圈为一个整体,且内、外圈具有锥形滚道,具有承受径向载荷和双向载荷、大载荷的特点,广泛应用在驱动桥主减速、风电主轴、轨道车辆轴承等领域。由于工作环境的影响,双列圆锥滚子轴承受到外部载荷变化的影响,轴承内部接触发生变化,引起轴承内部力学特性的变化,而内部接触力学分析是轴承设计时基础,直接影响轴承的整体性能及服役寿命。因此,开展双列圆锥滚子轴承对其力学性能影响具有重要的研究意义和工程实用价值。
国内外学者对圆锥滚子轴承开展较为系统且大量的研究。国外,Hertz [1] 研究了两个弹性体接触的局部应力和变形等问题,提出了经典解。Goodman [2] 对轴承疲劳损坏研究,得到轴承的疲劳破坏与方向和剪应力之间的联系。Liu [3] 给出了圆锥滚子轴承在轴向、径向及力矩载荷作用下滚动体所受负荷分布的计算方法。Cretu [4] 等运用矢量计算方法,研究了圆锥滚子轴承在承受不同的轴向载荷和不同转速的工况下轴承内部载荷分布规律。Yamashita [5] 等考虑润滑油的油膜厚度对圆锥滚子轴承的影响,给出了轴承接触载荷分布的变化规律。
目前国内,米俊、夏伯乾 [6] 类似于切片的研究方法,将内部接触应力与外载荷的关系进行迭代计算,得到圆锥滚子轴承滚动体与内、外圈滚道的接触应力。张磊 [7] 等人基于Hertz接触理论,分析了圆锥滚子轴承在承受重载下的工况,得到了滚动体与内、外滚道的接触应力分布状态。罗继伟、张俊杰 [8] 通过圆锥滚子轴承的载荷分布以及滚动体与滚道的接触变形,对接触应力的计算方法进行简化。张敬东、起雪梅 [9] 等人利用Romax软件分析了车辆变速器在不同档位状态下圆锥滚子轴承滚动体与内、外圈的接触应力值。王彦伟,罗继伟 [10] 等建立了圆锥滚子轴承整体接触力学模型,分析了滚动体与内、外圈滚道之间的接触应力及接触区域的形状。刘德昆 [11] 以高速列车轴承箱中的双列圆锥滚子轴承为研究对象,给出了不同载荷下双列圆锥滚子轴承内部接触载荷的分布规律。顾鑫鑫 [12] 应用“切片”法,建立了圆柱滚子轴承接触力学解析模型,分析了解析模型在偏载工况下的接触应力值,并通过ANSYS软件验证解析模型的准确性。
本文针对外部载荷变化引起双列圆锥滚子轴承引起的力学性能问题,以某型双列圆锥滚子轴为研究对性,基于轴承载荷计算公式获得轴承载荷分布作为单列轴承分析的载荷边界,建立最大承载区域的双列圆锥滚子轴承接触分析模型,在此基础上,分析不同载荷作用下的对其接触力学特性的影响。
2. 双列圆锥滚子轴承力学建模
2.1. 双列圆锥滚子轴承单体载荷计算
双列圆锥滚子轴承主要由外圈、分体式内圈、滚动体组成,且内、外圈均具有锥形滚道,轴承主结构见图1。双列圆锥滚子轴承的整体主结构尺寸如表1所示。

Figure 1. Structure drawing of double row tapered roller bearing
图1. 双列圆锥滚子承结构示意图

Table 1. Double row tapered roller bearing construction dimensions
表1. 双列圆锥滚子轴承结构尺寸
圆锥滚子轴承载荷分布通常指的是外载荷作用于轴承上,轴承各滚动体上所承受的负荷。施加在轴承上的外载荷主要先作用在轴承的某个套圈上,然后通过滚动体传递到另一个套圈上,而滚动体承所承受的载荷大小主要由轴承的尺寸结构参数和外载荷的类型决定。本节分析双列圆锥滚子轴承与轴承旋转轴线相垂直的载荷 [13]。
当滚动体的径向载荷的作用线与其中心线重合时,在这一条重合线上只有下半圈的滚动体存在载荷作用现象,而上半圈的滚动体不承受载荷。在图2中,在径向载荷
的作用下,下方底部滚子受到最大载荷
,
,沿着顺时针为负值,沿着逆时针方向为正值,在分析这种静不定问题时,在外载荷
和滚动体载荷
作用下处于平衡状态,可以得到:
(1)
式中,
,
表示标号为i的滚子中心线与径向载荷作用线方向的夹角。式中,
表示与载荷作用
线夹角为
位置的滚动体所承受的接触载荷。
式中,l为轨道不平顺波长,单位m;r为车轮半径,单位m。
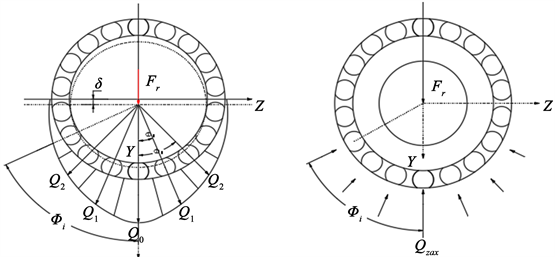
Figure 2. Load distribution of tapered roller bearing under radial load
图2. 圆锥滚子轴承在径向载荷下的载荷分布
若不考虑套圈变形,角度
处的变形协调条件是
(2)
式中,
表示与径向载荷作用线方向夹角为
处的总弹性变形量;
表示沿径向载荷作用线的滚子与内外滚道接触处的总弹性变形量。
由接触载荷与变形关系可得
可得
(3)
(4)
代入计算得
(5)
式中,
负荷分布径向积分;z表示滚子个数。
(6)
要分析圆锥滚子轴承在游隙为零的情况下,分析滚子在径向载荷作用下的应力分布,将轴承结构参数代入式(5)中可得:
(7)
对于有着正常径向游隙的向心滚子轴承,近似公式如下:
(8)
轴承承受载荷时,其滚子的受力情况如图2所示,设滚动体与内、外滚道和挡边的接触载荷分别为
、
和
,每个接触载荷可以分解为两个向量:轴向向量和径向分量,它们的接触角分别为
、
和
。
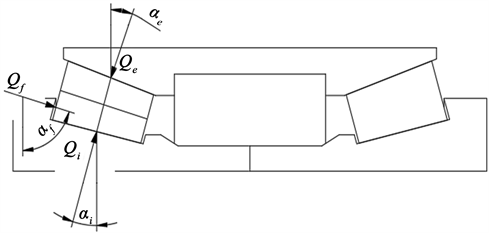
Figure 3. Stress diagram of double row tapered roller
图3. 双列圆锥滚子受力图
当滚子平衡时,它们的关系是
(9)
根据图3所示列出圆锥滚子受力的平衡方程:
(10)
解方程得:
(11)
(12)
式中,
,
。
由以上的推导公式可知,如果内滚道的接触应力计算出来,那么外滚道与滚动体和内滚道挡边与滚动体的接触应力也可以通过力学平衡方程得到。
2.2. 双列圆锥滚子轴承单体有限元模型
轴承材料为GCr15,根据表1中的双列圆锥滚子轴承整体结构尺寸建立三维模型,建模需对轴承进行部分简化。考虑到轴承为周期对称结构,并且双列圆锥滚子轴承的结构复杂、滚子数量较多的特点,将双列圆锥滚子轴承模型进行部分简化,建立的模型为双列圆锥滚子轴承的1/18,且忽略对计算结果影响较小的倒角、凹槽、保持架等。单体三维模型如图4。
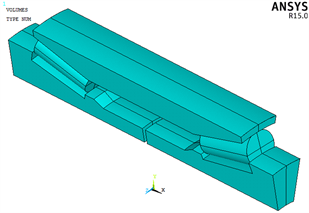
Figure 4. Single body ANSYS model of double row tapered roller bearing
图4. 双列圆锥滚子轴承单体Ansys模型
双列圆锥滚子轴承单元中采用三维Soild45六面体单元,采用扫略网格划分,对滚动体与内、外套圈滚道接触区域进行切片处理,最小网格尺寸为0.5 mm。双列圆锥滚子轴承的有限元模型中共包含网格数70,225,节点数82,782,网格划分后的模型结果如图5(a)所示。
 (a) 轴承网格划分
(a) 轴承网格划分  (b) 网格局部放大图
(b) 网格局部放大图
Figure 5. Single mesh model of double row tapered roller bearing
图5. 双列圆锥滚子轴承单体网格划分模型
接触对设置单元选用接触单元CONTA174和目标单元TARGE170来定义滚动体与套圈滚道的接触,具体如图6所示。
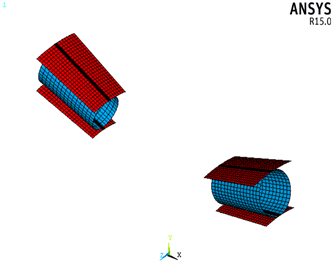 (a) 滚子与滚道接触
(a) 滚子与滚道接触  (b) 内滚道端面接触
(b) 内滚道端面接触  (c) 滚子与内圈挡边接触
(c) 滚子与内圈挡边接触
Figure 6. Single contact pair setting of double row tapered roller bearing
图6. 双列圆锥滚子轴承单体接触对设置
考虑实际工作与装配,轴承外圈固定,为全约束,限制6个自由度;内圈旋转,约束内圈表面节点的z方向的平动自由度;对内圈施加载荷,将内圈底面的所有节点耦合x、y方向位移,并在相应的耦合节点上施加径向力和轴向力。如图7。
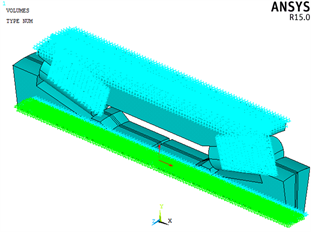
Figure 7. Finite element modeling of inner-loop coupling and outer-loop fully constrained
图7. 内圈耦合、外圈全约束有限元建模
本文的研究主要思路如图8所示。
3. 双列圆锥滚子轴承接触力学特性的影响
3.1. 额定载荷对轴承单体接触力学特性影响
通过正常工作条件下载荷进行计算,获取双列圆锥滚子轴承载荷边界 [14]。为了研究圆锥滚子轴承单体在额定载荷下的力学性能变化,通过对静载荷作用条件下双列圆锥滚子轴承内部载荷分布的分析,得到在额定载荷以及双列圆锥滚子轴承游隙为零的状态下,此轴承单体有限元模型内圈承受径向载荷为1011 N,轴向载荷为455 N。
通过ANAYS仿真得出双列圆锥滚子轴承滚动体与内、外滚道之间、滚动体与内圈大挡边和内圈端面的等效应力和接触应力。等效应力云图,如图9所示。接触应力云图,如图10所示。仿真分析结果与Hertz理论值结果对比如表2所示,通过结果对比,Matlab赫兹接触理论和ANSYS有限元模型计算出的滚动体与仿真分析内、外圈接触应力值结果基本一致,且数值上的存在的最大差异未超过10%,并在合理的应力值范围内,验证有限元接触模型的准确性。

Table 2. The contact stress value of ANSYS is compared with the numerical calculation result
表2. ANSYS的接触应力值与数值求解计算结果对比
3.2. 径向载荷对轴承接触性能的影响分析
开展不同径向载荷对双列圆锥滚子轴承接触应力分析。如表3所示。设定固定轴向载荷为500 N,径向载荷的变化范围为1000~4500 N。计算结果如图11所示,从图中可以看出:轴向力不变,随着径向载荷的增加,轴承左、右两侧滚动体与内、外圈滚道之间的最大接触应力增大;接触应力基本呈线性增加;轴承左、右两侧滚动体与内圈的接触应力值均大于左、右两侧滚动体与外圈的接触应力值。轴承右侧滚动体与滚道接触应力值均大于左侧滚动体与滚道接触应力值。基本一致,均无较大差别,数值差异未超过16%。说明双列圆锥滚子轴承在承受外载荷时内圈存在一定的倾斜;双列圆锥滚子轴承内圈两侧端面之间的接触应力值较小,且随径向载荷的增加而减小;轴承左、右两侧滚动体与内圈滚道挡边之间的最大接触应力随着径向载荷的增加而增大。
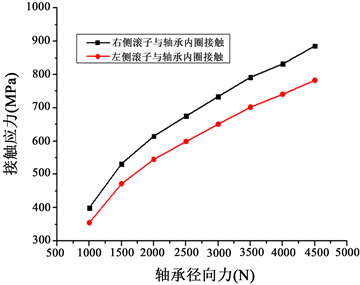 (a) 滚子与内圈的接触应力变化
(a) 滚子与内圈的接触应力变化  (b) 滚子与外圈的接触应力变化
(b) 滚子与外圈的接触应力变化 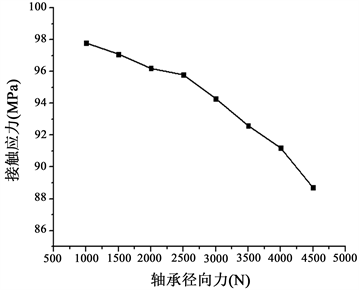 (c) 内圈端面的接触应力变化
(c) 内圈端面的接触应力变化 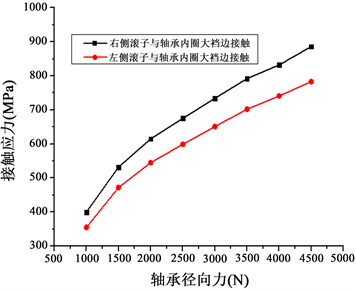 (d) 滚子与内圈的档边接触应力变化
(d) 滚子与内圈的档边接触应力变化
Figure 11. Variation curve of internal contact stress of bearing singles with radial load
图11. 轴承单体内部接触应力随径向载荷的变化曲线
4. 结论
本文基于有限元理论建立并建立双列圆锥滚子轴承单体有限元模型,分析额定载荷下滚动体与内、外圈滚道的接触应力以及径向载荷的影响规律,可得如下结论:
1) 双列圆锥滚子轴承单体有限元模型计算出在一定外载荷条件下,滚动体与内、外圈滚道的接触应力值,并与Hertz接触理论对比验证,接触应力值基本一致,且数值上最大差异均未超过10%,并在合理的区间范围内,验证有限元模型的准确性。
2) 径向力增大时,轴承内部滚子与滚道,滚子与内圈挡边之间的接触应力呈线性增加,两个内圈的端面之间的接触应力减小,这是由于过大的径向力会使的轴承两个内圈向相反的方向移动,从而减小内圈端面的接触应力。
NOTES
*通讯作者。