基于B/S架构的航线规划仿真系统的设计与实现

Design and Implementation of Flight Route Planning Simulation System Based on B/S Architecture

摘要: 在航线规划设计过程中，设计者和飞行员需要通过航线数据的计算和显示，查看和分析航线设计结果，以及机动改变航线点后的结果。本文通过研究二维坐标系下不同转弯方式的航线点数据的计算方法，完成基本的领航计算，确定每一个航段的各项飞行诸元，最终设计实现了一种基于B/S航线规划仿真系统，能够实时计算、显示和管理航线及航线点数据，指导航线规划设计工作。

Abstract: In the course of route planning and design, designers and pilots need to view and analyze the results of route design through calculation and display of route data, as well as the results after maneuvering the route points. By studying the calculation method of the route point data of different turning modes in the two-dimensional coordinate system, this paper completes the basic navigation calculation, determines the various flight elements of each segment, and finally designs and implements a B/S-based route planning simulation system. It can calculate, display and manage route and route point data in real time, and guide route planning and design work.

1. 引言

在飞机领航系统的航线规划设计过程中，需要对航线设计进行仿真分析，计算和显示航线数据及具体航线图形，便于设计者和飞行员查看和分析航线设计结果。航线仿真主要是对整个飞行过程中，整体航线的各个航线点的航行诸元、转弯数据等进行计算，并绘制各个航路点之间的连接线。传统的航线规划通常只为操作人员提供单一的航路生成方式，且其制定的飞行航路忽略了飞行器的转弯过程，也很少有对单点进行配置生成航线的方法。本文基于B/S架构，提供多种编辑航线手段，允许操作人员实时修改航线点数据从而修改航线视图，并对航线及航线点数据进行管理 [1]。

2. 系统功能设计

航线仿真系统基于B/S架构开展设计与实现，在数字地图中实现飞机飞行航线数据及转弯点数据计算、航线绘制和修改、航线管理等功能，能够以图形化方式或表格编辑方式完成任务航线的建立与维护 [2]。

1) 航线及转弯点数据计算

航线距离及时间：计算从上一个转弯点到当前转弯点的飞行距离和飞行时间；

航线总距离及时间：计算从起始点到终点总的飞行距离和飞行时间；

转弯点坐标：在数字地图中某一点的经纬度数据，需要通过在数字地图中拾取坐标点或者用户输入；

转弯点航向：飞机纵轴前方的延长线为航向线，飞机所在位置的经线北端顺时针至航向线的夹角；

转弯点空速：飞机在该转弯点相对于空气的速度；

转弯坡度：飞机转弯时，机身向转弯中心倾斜，也就是向内侧倾斜的角度；

转弯半径：在空速和坡度限制下，计算飞机转弯时距离转弯中心的距离；

转弯方式：如果用户需要显示转弯弧，则可以设置为压点、向点、绕点转弯，若用户不需要显示转弯弧，则可以设置为直线，此时将不计算转弯点数据。

2) 航线绘制及修改

通过计算航线点的转弯角度、转弯圆弧的起始点和终止点，实现在不同转弯方式下，自动计算转弯方向，绘制航线点形成的圆弧和直线，从而形成航线。对已制定的航线进行修改，能够在数字地图上拖拽航线点，修改其经纬度，在航线列表中修改航线转弯点经纬度、坡度、空速、飞行方向数据并重新进行航线的计算和绘制。

3) 航线管理

利用数据库对航线数据进行存储，添加，删除，修改和查询。数据库主要包括机场数据表单、航线数据表单、航段数据表单、转弯点数据表单。机场数据库表单为机场名称、经度、纬度等，航线数据表单包括航线名称、航线飞行时间、航线飞行距离，航段数据表单包括航段名称、航段飞行时间、航段飞行距离、航向；转弯点数据表单包括转弯点名称、经度、纬度、地标名称、转弯方式(绕点、压点、向点)、转弯方向、高度、速度、坡度等 [3]。

3. 转弯方式概述

常见的转弯方式包括压点转弯、绕点转弯和向点转弯。

1) 压点转弯

飞机到达预定转弯点上空时，立即开始按预定转弯坡度转弯，当转到预定改出航向时，改平转弯坡度对正该航向飞行。在采用这种转弯方式时，航路点自身是转弯弧的起始点，如图1所示。

Figure 1. Press point turn

图1. 压点转弯

2) 绕点转弯

在飞机起飞前进行地图作业时，根据飞机的飞行速度，计算出预定转弯坡度对应的转弯半径，以预定转弯点为圆心，以该半径画一弧线，使对向该转弯点的航线外切与该弧线的一个点上。飞行中，当预定转弯点位于飞机正侧方，飞机开始转弯；当对正预定航向时改出转弯，对向下一段航线飞行。在采用这种转弯方式时，航路点自身为圆心，如图2所示。

Figure 2. Turn around

图2. 绕点转弯

3) 向点转弯

飞机在经过此航路点时，先进行转弯，再在航路点上完成转弯，一般在飞完前一段航程之后，需要转弯对正下一段航线使用向点转弯。在这种转弯方式中，航路点自身是转弯弧的结束点，如图3所示。

Figure 3. Turn to the point

图3. 向点转弯

4. 航线数据计算方法及实现

绘制航线需要对直飞过程进行直线绘制，对转弯飞行过程绘制转弯弧段，并与直飞过程相连，绘制出连续的航线，因此需要重点计算转弯弧段数据 [4]。

1) 转弯诸元计算

转弯半径计算：见式1，V为飞机飞行速度(米/秒)，γ为转弯坡度(度)，g为重力加速度(9.81米/秒²)

$R=\frac{V^2}{g\cdot tg\gamma }$ (1)

转弯时间计算：其中转360度时间见式2，R为飞机转弯半径(米)，ZW为飞机转弯角度(度)

$T_{360˚}=\frac{2\pi R}{V}$ (2)

转任意角度时间见式3

$T_{ZW}=T_{360˚}\cdot \frac{ZW}{360}$ (3)

2) 转弯弧段计算及实现

转弯弧段数据包括默认转弯方向，转弯点圆心，圆上转弯弧段的起始点和结束点，转弯角度 [5]。

· 默认转弯方向：

设P_i点为上一个航段的结束点，从该点开始，途径P_i+1点进行转弯，到P_i+2点，分别计算P_iP_i+1和P_i+1P_i+2的航向，相减得到夹角α，则当α > 180˚时，P_i+1点的转弯方向为左转，如图所示，当α < 180˚时，P_i+1点的转弯方向为右转，如图4所示。

Figure 4. Turning direction calculation

图4. 转弯方向计算

· 转弯点圆心：当P_i+1的转弯方式为压点转弯时，设圆心点为C，如图5所示，已知P_iP_i+1航向，通过±90˚ (右转为+，左转为−)，得到P_i+1C的方向，根据上述求得的转弯半径R，可得到C点坐标；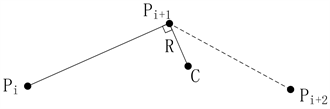

Figure 5. Calculation of the turning center of the pressure point

图5. 压点转弯圆心计算

当P_i+1的转弯方式为绕点转弯时，该转弯点坐标即转弯点圆心坐标；

当P_i+1的转弯方式为向点转弯时，如图6所示，如果P_i+2是压点转弯或是结束点，则可计算P_i+1P_i+2航向，通过±90˚ (右转为+，左转为−)，得到P_i+1C的方向，通过转弯半径R，可得到C点坐标；如果P_i+2是绕点转弯或是向点转弯，则先计算下一个点的转弯弧起始点，直到不是向点转弯，再通过反向递推方式，由下一个点的转弯弧起始点计算P_i+1的转弯点圆心C。

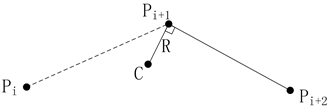
Figure 6. Calculation of the center of the turning point

图6. 向点转弯圆心计算

· 转弯弧起始点：

当P_i+1的转弯方式为压点转弯时，该转弯弧起始点为该点坐标；

当P_i+1的转弯方式为绕点转弯时，如图7所示，设转弯弧起始点为P_i+1S，需要求C点到P_i+1S的方向角 $\angle \beta$ 。已知P_i和C点坐标，可得两点距离 $\left|P_{i}C\right|$ ， $\angle \alpha$ 为P_iP_i+1S和P_iC的夹角， $\angle \gamma$ 为P_iC的方向角，则

$\angle \alpha =\arcsin \left(R/\left|P_{i}C\right|\right)$

$\angle \beta =\angle \gamma -{90}^{\circ }-\angle \alpha$(右转时)

$\angle \beta =\angle \gamma +{90}^{\circ }+\angle \alpha$ (左转时)

可得 $\angle \beta$ ，已知P_i+1SC为转弯半径，则可求得P_i+1S坐标，转弯角度即 $\angle \beta$ 。

Figure 7. Calculation of the starting point of the arc around the point

图7. 绕点转弯弧起始点计算

当P_i+1的转弯方式为向点转弯时，通过上述转弯点圆心的计算，得到转弯点圆心坐标后，则可参照绕点转弯时的计算方式，得到该转弯弧起始点坐标。

· 转弯弧结束点

当P_i+1的转弯方式为压点转弯时，如图8所示，设转弯弧结束点为P_i+1E，需要求C点到P_i+1E的方向角 $\angle \beta$ 。已知C和P_i+2点坐标，可得两点距离 $\left|C{P}_{i+2}\right|$ ， $\angle \alpha$ 为P_i+2P_i+1E和CP_i+2的夹角， $\angle \gamma$ 为CP_i+2的方向角，则

$\angle \alpha =\arcsin \left(R/\left|C{P}_{i+2}\right|\right)$

$\angle \beta =\angle \gamma -{90}^{\circ }+\angle \alpha$(右转时)

$\angle \beta =\angle \gamma +{90}^{\circ }-\angle \alpha$ (左转时)

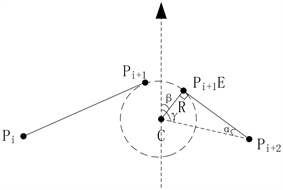
Figure 8. Calculation of the starting point of the turning arc

图8. 向点转弯弧起始点计算

可得 $\angle \beta$ ，已知CP_i+1E为转弯半径，则可求得P_i+1E坐标，转弯角度即 $\angle \beta$ 。

当P_i+1的转弯方式为绕点转弯时，通过上述转弯点圆心的计算，得到转弯点圆心坐标后，则可参照压点转弯时的计算方式，得到该转弯弧结束点坐标。

当P_i+1的转弯方式为向点转弯时，该转弯弧结束点为该点坐标。

5. 仿真系统实现

通过设计和实现上述计算算法，创建航线数据库，搭建B/S架构的仿真系统。在应用过程中，首先添加起升点和降落点。一般情况下，起升点和降落点均为机场数据，因此在具有机场数据库的情况下系统将自动从机场数据库中读取最近的机场经纬度数据。

采用GIS地图获取地图图层，操作者可以在图层上点选转弯点位置，获取转弯点的经纬度。也可以在列表中可以点击实际数据进行编辑，调整转弯点的经纬度、高度、速度、升降率、坡度和转弯方向、转弯方式等，如图9所示。

当转弯点个数大于1时，仿真系统自动计算该点的转弯方向、转弯半径和前一个转弯点的转弯弧段，并将直线和弧段通过GIS图层的方式绘图显示，如图10所示。通过经纬度和速度数据，可以计算出两个转弯点之间的飞行时间、飞行距离和方向数据，并在地图中航线段上显示。

Figure 9. List of route drawing

图9. 航线绘制列表

Figure 10. Route drawing display

图10. 航线绘制显示

6. 总结

本文给出了一种基于BS架构的航线规划仿真系统的设计与实现方法，能够为操作人员在设计航线过程中提供多种编辑转弯点的手段，既可以采用地图取点的方式，也可以采用手动录点的方式，便于操作人员使用。系统根据操作人员所设定的航路点及转弯方式和参数，实时计算航线点的转弯诸元数据、转弯弧段绘制数据等，并分段绘制航段，形成整体航线，从而达到指导航线规划设计工作的效果。