1. 引言
随着全球经济一体化进程的不断加快,各个金融主体之间的联系越来越紧密,普遍存在着错综复杂的关联关系。金融主体之间的关联关系,一方面能够给各金融主体带来更多的机会和收益;另一方面也给金融风险的产生与传染提供了条件和渠道。复杂网络是通过线将大量的点配对并连接起来的抽象化表现。现代金融体系作为一种极其复杂的网络,可以利用复杂网络的理论、方法以及技术来分析金融网络中的相关问题。越来越多的学者通过复杂网络来描述金融市场间的错综复杂关系,通过各种金融关联将网络中的所有节点相互连接起来,连接各个节点的边反映各个金融节点之间的风险传播问题。基于复杂网络来分析金融风险,能够研究不同风险传播,可以清晰地分析金融市场风险传播的趋势,直观形象地刻画出金融系统内在的联系,在描述市场间的关联结构和交互作用具有明显的优势。复杂网络基本理论已经被广泛运用到经济、管理和生物等多个领域,现已成为专家学者们刻画社会网络、信息网络和经济金融网络的一种重要工具,同时也为研究经济发展和风险管理问题提供了新颖的视角。
金融机构之间的风险传播已经造成不同类型和规模的机构出现“一损俱损”的局面,当前国内外金融危机的案例层出不穷,世界各地都非常重视金融风险的防控,已把维护金融安全提到了治国理政的高度。因此,对金融风险传播的深入研究和防控,具有很强的现实意义。同时,在金融风险传播过程中,正确的政策引导或救助对于金融机构抗击风险具有重大意义。
在全球经济金融长期处于不确定性的背景下,结合现实社会中,有的主体存在一定的风险,但是选择将其隐蔽不公开(本文称之为处于潜在风险状态的主体),所以为了更贴合现实中的金融系统以及更好地理解其动力学特征,本文从网络的视角出发,基于经典的传染病动力学模型,在匀质网络和异质网络上分别构建金融风险传播的改进的SEIR模型,并对平衡点的存在性和稳定性以及基本再生数进行分析。
本文的研究结构为:第二部分介绍文献综述;第三部分构建匀质网络和异质网络上的金融风险传播的改进SEIR模型,通过理论分析,得到模型的重要性质;第四部分为模拟仿真,通过构建实际的金融网络和四种典型的人工合成网络,对理论结果进行验证;第五部分进行总结。
2. 文献综述
随着大数据和网络科学的发展,金融风险扩散逐渐成为研究热点。下面将从金融系统的网络特性分析,金融风险传播影响因素,基于传染病动力学的金融风险传播三方面介绍相关研究工作。
金融系统的网络特性方面:复杂网络可以描述复杂系统个体间的连接关系,在其被引入金融系统领域后就展现出蓬勃的发展趋势。许多研究这运用复杂网络理论探究不同类型金融系统拓扑结构及其演化规律,如股票市场、外汇市场、期货市场等。杨睿(2014) [1] 构建了全球股票市场网络模型,得出股票市场网络具有无标度属性的结论。石大龙(2015) [2] 通过对我国的大额支付系统构建网络,发现银行间资金流的交易金额网络具有无标度特性,但交易笔数网络不具有无标度特性。巴曙松等(2014) [3] 运用复杂网络理论的相关知识,分别对中国的不同类别银行、不同地区银行的支付网络的拓扑结构做了实证分析,发现这两个网络具有了“小世界网络”的典型特征。但是现实情况是各个主体间的联系错综复杂,网络结构也多种多样。
金融风险传播影响因素方面:金融系统间连接关系对于风险传播起到桥梁作用,Gai等(2010) [4] 通过构建银行网络模型,发现银行之间的高连通性能够降低风险传播的概率。但是邓超等(2014) [5] 基于随机网络,经过研究发现银行之间紧密的关联关系反而加大了金融风险的传染。另外金融个体的行为和决策影响风险传播的效应,Jiang等(2018) [6] 基于复杂网络传播动力学理论,研究信用风险传播的内在违约问题,建立的模型能够有效地反映个体的风险传染程度,并深入分析了个体风险态度、个体风险抵御能力等对信用风险传播的影响。罗暘洋和李存金(2020) [7] 通过构建银行同业资金网络实证分析银行违约风险的传染效应,发现银行资产规模、同业业务量和风险加权资本对风险传染效应有显著正向影响。
基于流行病传播过程与金融风险扩散的相似性 [8] ,许多学者考虑不同的传播机制并研究相应金融风险传播过程,比如Garas等(2010) [9] 利用SIR传染模型来研究金融危机在世界各国间扩散,金融危机的扩散方式非常繁杂,曾志坚和吴汪洋(2018) [10] 基于复杂网络方法构建亚太经济合作组织成员国之间的贸易网络,并在此基础上运用SIRS模型对金融危机在贸易渠道上的传染进行分析,最后得到金融危机在贸易渠道上具有传染迅速、持续时间长的特点,贸易网络具有小世界效应等的结论。胡志浩和李晓花(2017) [11] 将传播动力模型SIRS引入到无标度的金融网络中,探讨了模型参数如感染率、治愈率、免疫失效率和网络紧密度对风险传染的影响。刘晓宇和吕琳(2018) [12] 建立了一类SIR和SIS组合的金融市场风险传染动力学模型,对模型平衡点的存在性和稳定性以及风险传染阈值进行了分析。考虑到潜在危险个体,徐凯(2019) [13] 构建关联信用风险传染的改进动力学SHIR模型,并在此基础上讨论了关联信用风险传染的影响机制。
3. SEIR模型构建与理论分析
本节我们结合传染动力学SEIR模型,来分析金融网络中的风险传播模型。基于网络结构的不同,我们分别构建了匀质和异质两种网络结构,并分别开展理论分析。
根据金融系统在金融风险扩散过程中所表现的不同状态,将其分为以下四类:
1) 正常状态S:处在正常状态的主体是指在金融网络中,自身的风险较低,但容易受到与之有联系的高风险主体影响的主体,从而具有变为高风险主体的潜在可能性。这部分主体在金融网络中数量比较多,往往通过这些主体在网络中形成多米诺骨牌效应,从而对整个金融网络产生巨大的危害。
2) 潜在风险状态E:处在该状态下的主体是指已经被传播风险,其风险处于较高水平。本文这里的潜在风险状态不具有传播性,但是能通过和正常主体之间的联系来分担自身的风险。随着外部环境和自身内因的变化,经过一段时间,其中自身抗风险能力较弱的主体有可能转变为风险个体I,自身抗风险能力提高而比较强的部分E主体恢复为正常状态。
3) 风险状态I:处于风险状态的主体是指在金融网络中,自身风险较高,而且能通过不同联系对与其关联的个体产生负面影响的一类主体。这部分主体在网络中的结构和数量都能显著地影响金融风险在金融网络中的传播效应。该部分主体在网络中所占比例不仅表征了金融风险的传染强度,而且所占比例的变化显示了金融风险在网络中的演化过程。
4) 移出状态R:在金融网络中,这类主体在金融风险的识别和控制方面具有相对优势和经验,在一定时期内可以通过采取有效的措施,能够规避金融风险的传播,是具有风险抵御能力的一类金融主体。但这种状态并不是永久保持的,在各种内外因素的作用下,免疫能力逐渐变弱甚至丧失。移出状态的主体也会逐渐演变为其他状态。
各状态之间的转换规则如下:
正常金融个体通过与风险个体连接关系(借贷关系,持有共同资产等),使得金融风险进一步扩散,该正常金融个体以概率
变为潜在风险个体,以
的概率变为风险个体。潜在风险个体通过自身能力(运行、筹资等)或得到外部政策支持或救助,控制金融风险的扩散,以概率
成功恢复为正常个体,而以
的概率变为风险个体。处于风险状态的个体也通过采取一系列的措施,以概率
转变为移出个体,一般假设
。移出主体并不能永久的抵御金融风险,还会以
的概率变为金融网络中的正常个体,重新面对金融风险的传播危机。风险传播模型如图1所示。
模型涉及到的各参数设定如下:
表示正常状态主体被传播风险而变成潜在风险状态主体的比例;
表示若潜在风险主体自身能力提高或得到救助后,潜在风险状态主体转变为正常状态主体的比例;
表示正常状态的主体与风险状态主体接触后被传染的概率;
表示潜在风险状态主体移出率,
为潜在风险状态主体的潜伏周期,周期的倒数就是移出率,而移出率是不断变化的,为了简化研究,这里用转换率的平均值,即用平均转换率表示移出率;
表示恢复率,即风险主体恢复为移出主体的概率;
表示移出主体变为正常主体的比例。

Figure 1. SEIR risk communication model
图1. SEIR风险传播模型
3.1. 基于匀质网络的SEIR模型
匀质网络是指,金融个体的连接关系相似,即合作、连接对象相同或相等。对应在复杂网络中即为匀质网络。因此,我们将网络中的金融个体分为四类:
,
,
和
,分别为正常主体、潜在风险主体、风险主体和移出主体的相对密度,且
。由平均场理论和均匀网络,构建金融风险传播的SEIR基础动力学模型,可得风险传播的动力学方程组:
(1)
令系统(1)的右边均等于零,可解得出匀质网络的无风险平衡点为
,非零风险平衡点为
,其中,
,
,
,
下面,利用下一代矩阵方法来计算基本再生数
。
系统可简写为:
(2)
其中,
表示被感染仓室,
表示其他仓室。
表示新风险状态主体的出现率,
表示主体迁移率。
这里计算基本再生数
时只涉及到潜伏者仓室
和染病者仓室
。
首先,划分X向量,
(3)
根据文献 [14] 中的引理1可得:
(4)
则无风险平衡点
下的雅可比矩阵分别为:
(5)
所以,
,且当
时,
恰好就等于非零风险平衡点上
的倒数。
接下来证明无风险平衡点的局部渐进稳定性。
系统可简写为,
(6)
所以在点
处的雅可比矩阵为
此时,矩阵对应的一个特征根为
,另外两个特征根满足特征方程
.
当
,即
时,根据
可以判断,特征方程
的两个解都小于0,也就是说在点
处的三个特征根均为负,说明点
局部稳定。
反之,当
时,在点
处的三个特征根中正负号不相同,此时点
不稳定。
考虑无风险平衡点
的全局稳定性。首先构造李雅普诺夫函数:
。
再将
关于模型(1)对t求导可得,
(7)
所以,当
时,
,且
除
外无模型(7)的其他轨线,
全局渐近稳定。反之,当
时,
不稳定。
下面讨论非零风险平衡点
的局部稳定性。
在点
处的雅可比矩阵为
所以,对应的特征方程为
.
其中,
从而可以进一步证明,
,再根据Routh-Hurwitz判定定理可知,特征方程
的根均为负,故模型(6)在非零风险平衡点
处是局部渐近稳定的。
3.2. 基于异质网络的SEIR模型
考虑到现实的金融网络许多具有无标度特性,即存在度非常大的个体。因此,我们基于网络度进行分类,记为:
和
,分别为度为k的正常主体、潜在风险主体、风险主体和移出主体的相对密度,且
。
可以得到异质网络下的金融风险传播的动力学方程组:
(8)
其中,
,表示t时刻随机取一条边与感染节点相连接的概率。
表示网络的平均度。
得出异质网络的无风险平衡点为
,非零风险平衡点
,其中,
,
,
,
,
.
将
代入,
满足自相容条件,可得
(9)
显然
是方程的一个平凡解,且
连续可微,
关于
关严格单调递增。
故当且仅当
,即
时,方程存在唯一非平凡解
。且其中,
。
接着讨论无风险平衡点的局部稳定性。
系统(8)可简写为:
(10)
故在点
处的雅可比矩阵为
其中,
为n阶单位矩阵,
为n阶零矩阵。
显然,矩阵
有n个特征值等于
。
对矩阵作行列相似变换,所得矩阵与原矩阵有相同特征根。
所以,矩阵
有n个特征值等于
,其余n个特征值是矩阵
的特征值。
对矩阵
作行列变换,可得矩阵
有
个特征值等于
,第3n个特征值是
.
因此,当
时,矩阵
的3n个特征根均为负值,说明系统(10)的无风险平衡点
是局部渐近稳定的。反之,当
时,点
不稳定。
对于无风险平衡点
的全局渐近稳定性的证明,先构造李雅普诺夫函数,
(11)
再将
关于模型对t求导得,
(12)
当
时,
,且
除
外无模型(10)的其他轨线,所以
全局渐近稳定。
以下是对风险传播的持久性的证明。
首先,定义
容易证明,集合X是正不变集,从而,对
,
,
,
,一定对任意
有,
,
,
,且由比较定理可得
。
因此,集合
也是正不变集。进一步可知,存在集合X的紧子集B,使得从X中出发的任何一个解,将进入并永远停留在B中。对此紧子集B,易证满足文献 [15] 中紧性条件(C4.2)。
定义
,
,
,
这里
是系统(8)的
极限集。将系统(8)限制在
上,得到,
(13)
显然,系统(13)有唯一的全局渐进稳定的平衡点
,因此,
,显然
是一个孤立的非循环覆盖。最后,我们将证明平衡点
相对于
是弱排斥的,即相对于系统(8)任何一个初值从
出发的
解
,满足
。
从文献 [16] 中引理3.5的证明知,要使上式成立,只需证明
,其中
是系统(8)平衡点的稳定流形。若不然,则一定存在解
,使得
,
,
,
,当
因为对于
,由上式得一定存在
,
,
,
,
,
。
定义函数
,沿着系统(8)对
求导得
。
因此,
。注意到
,则有
,从而,当
时,有
,这明显与
导致
有界相矛盾。
4. 模拟仿真
4.1. 金融网络的构建
数据选自Wind数据库(收集时间:2021年8月10日)中2008年、2018年和2020年的沪深股票市场以及美国股票市场的wind金融类股票的日收盘价数据,并剔除掉缺失数据较多的金融机构,最终数据包括:沪深股票市场2008年52家机构的246个有效交易日的数据、2018年94家机构的243个有效交易日的数据、2020年116家机构的243个有效交易日的数据,美国股票市场2008年445家机构的238个有效交易日的数据、2018年651家机构的235个有效交易日的数据、2020年52家机构的779个有效交易日的数据。对日收盘价数据作如下处理。
根据股票i在第t个交易日的收盘价格
,得到股票i的价格收益率:
,并计算任意两个金融i与j之间的Pearson相关系数
。其中,
为统计平均。从而可以得到一个相关系数矩阵
。
但由于我国不是强型有效市场,所以利用证券市场信息所构建的金融网络存在噪音,需要去除噪音,使得该复杂网络中各节点间的风险传播更具真实性(对于美股数据而言则可省略这一步骤)。而基于随机矩阵理论的金融网络去噪方法,能够保留原始网络的关键信息(吴翎燕,2013)。具体步骤是先计算出相关系数矩阵
基于随机矩阵理论的最大、最小特征值
和
:
。其中,Q等于矩阵的行数除以列数(本文中
),
为矩阵中所有元素的方差。
先求得相关系数矩阵
的特征值和特征向量,再将处于
内的特征值全部替换为0,进而得出新的特征值序列
,然后根据新的特征值和特征向量计算出除去噪音后的相关系数矩阵
。最后,基于阈值方法确定金融网络。图2展示了六个网络(如:CHN2008代表2008年中国沪深金融网络;USA2008代表2008年美股金融网络)的最大连通子图包含的节点数随着阈值大小的变化情况。结合下图网络最大连通子图节点个数随阈值的变化趋势,考虑将沪深市场阈值设为0.5,而将美股市场的阈值设为0.25,也就是如果沪深股票数据的关系矩阵中的元素大于等于阈值0.5,则将其替换为1,否则为0;而美国股票数据的关系矩阵中的元素大于等于阈值0.25,则将其替换为1,否则为0,由此得到邻接矩阵,从而根据邻接矩阵构建金融网络。
表1和表2列出了六个网络的几个重要指标。以2008年的沪深金融网络为例,它形成了一个具有52个节点(其中3个为孤立的节点)、791条边的复杂网络。经分析得到该网络的拓扑特征如下:平均度为16.1,意味着网络中每个节点平均有16个邻居节点;平均聚集系数为0.8209,说明节点的聚集程度比较高,但较高的网络凝聚性也会使得风险传播的广度有所增大;平均最短路径为1.3,即任意两个节点基本都有直接的联系。整体来看,三个年份的沪深市场的金融机构个数都远远少于美股市场,六个网络的平均最短路径都偏小,说明各个金融机构之间的联系日益紧密,风险传播变得更加迅速。图3也展示了六个网络去除孤立节点之后的金融网络结构示意图,从图上也可以直观的看到,中国沪深股票市场的各个金融机构都在一个最大连通网络中,而2018年和2020年的美股金融网络均形成了一个包含较多节点的最大连通图和一个包含2个节点的连通子图的网络结构。网络中均表现为“强强联合”、两极分化的特征,度较高的节点个数较多,度低的节点个数较少,即具有较高的度的关键节点之间建立起了十分紧密的联系,而与具有较低的度的边缘节点的联系较少。

Figure 2. The variation of the number of nodes in the largest connected subgraph with the threshold
图2. 最大连通子图节点个数随阈值的变化情况
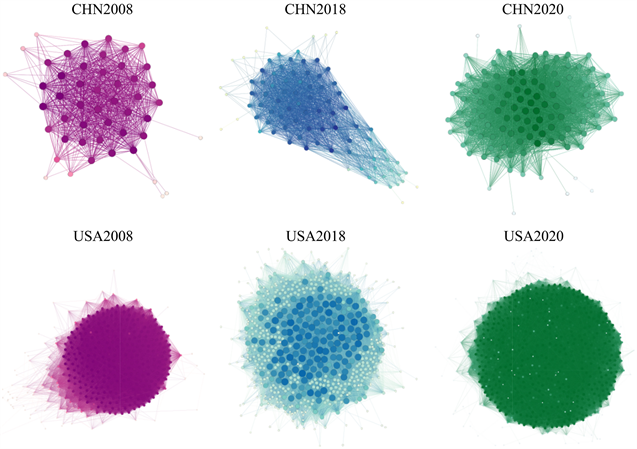
Figure 3. Structure diagram of various financial networks
图3. 各金融网络结构图

Table 1. Topological characteristics of Shanghai and Shenzhen financial network
表1. 沪深金融网络拓扑特征

Table 2. Topological characteristics of U.S. stock financial network
表2. 美股金融网络拓扑特征
4.2. 真实数据网络下的模拟仿真
下面分析不同基本再生数
下,利用Mean Field (MF)和Monte Carlo (MC)两种方法进行模拟仿真,并将四类状态主体的初始密度设为
,来分析四种不同状态主体的密度随时间的演化规律。图4所示为
情况下,六个金融网络中的四种不同状态(正常状态主体S、潜在风险状态主体E、风险状态主体I和移出状态主体R)的节点密度演化规律,这里考虑到沪深网络和美股网络的平均度差距较大,为了保证
,所以其中
也取不同的值分别为0.01、0.001,其余参数设为:
、
、
、
、
。可以看出,当
(具体的
分别为:2008年中国沪深金融网络0.2830;2018年中国沪深金融网络0.3908;2020年中国沪深金融网络0.6189;2008年美股金融网络0.2377;2018年美股金融网络0.2919;2020年美股金融网络0.4752)时,六个网络的密度曲线最终都到达无风险平衡点
,且由图像得知,S状态主体密度呈现出先降低再逐渐增加到1的趋势;E先增加后逐渐趋于0;I从最初的0.05快速减小到0;R先增大后又减小到0。横向来看,中国沪深市场和美股金融市场的三个网络的潜在风险状态E密度曲线的峰值越来越大,且美股金融市场网络中E密度曲线的峰值均大于沪深金融网络,2020年美股金融网络到达无风险状态平衡点相比其他网络所需的时间要更长一些。图5所示为
(具体的
分别为:2008年中国沪深金融网络2.8295;2018年中国沪深金融网络3.9083;2020年中国沪深金融网络6.1893;2008年美股金融网络11.8859;2018年美股金融网络14.5968;2020年美股金融网络23.7613)情况下的四种不同状态下的节点密度演化规律,沪深市场和美股市场的
分别取0.1和0.05,其余参数均不变。从图中可以看到最终平衡点风险状态主体的密度已经远大于初始设定值0.05,说明风险已经在网络中进行了扩散。在MC方法下,密度曲线都经过波动后逐渐趋于稳定状态。在MF方法下,所有I的密度变化都呈现先骤增再逐渐减小至稳定状态的趋势,分别看中国沪深市场的三个金融网络中的风险状态I的峰值和最终密度在逐年变大,美股市场的2008年金融网络的峰值大于2018年的,但差距很小,最终密度的稳定值也是越来越大的,这可能与各个金融机构之间的关系越来越密切有关。

Figure 4. When R0 < 1, the density of the four types of subjects under each network changes
图4. R0 < 1时,各网络下的四类主体密度变化

Figure 5. When R0 > 1, the density of the four types of subjects under each network changes
图5. R0 > 1时,各网络下的四类主体密度变化
图6所示为六个金融网络下风险状态主体I的密度随风险传播概率
的变化曲线,其余参数设定为:
、
、
、
、
。从图中可以很明显地看到,在MF方法下的风险状态主体I密度曲线都是高于MC方法下的,这可能是由于MC方法只能分析每一次算法过程中的具体状态主体的个数,而MF则是基于数量比例,所以这两种方法存在一定的差异性。在MC方法下,三个沪深市场金融网络的临界
分别为:0.04、0.02、0.01,而美股金融网络的临界
几乎为0,也就是说在相同条件下,美股金融网络更容易造成风险的传播,即使很小的风险传播概率也会导致金融风险迅速地在美股金融市场中传播。
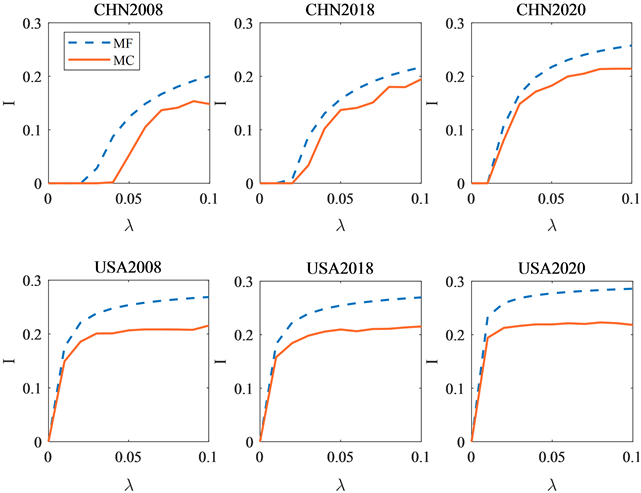
Figure 6. The change curve of the subject density of the risk state of the six networks with λ
图6. 六个网络的风险状态主体密度随λ的变化曲线
图7展示的是在六个网络中,利于MF和MC两种方法分析
取不同的值时,风险状态主体I的密度随时间变化情况。参数
、
、
、
,沪深市场和美股市场的
分别取0.1和0.05,
分别取0.1、0.5,从图像得出
与风险状态主体I密度成负相关关系的结论。正常状态主体受风险传播影响而变成潜在风险状态的概率越大,处于潜在风险状态的金融个体的密度就越高,而处在风险状态主体的密度则越小。
图8展示的是在六个金融网络中,利用MF和MC两种方法分析当救助率
取不同的值时,风险状态主体I的密度随时间变化情况。当其他参数:
、
、
、
、
,而救助率
分别取0.1和1时,从图中可以看出,在六个网络中都表现出随着
的增大,网络中的风险状态主体越来越少,风险传播效应减小,这与现实情况一致。也就是说,救助率越高,越能抑制金融风险的扩散。

Figure 7. Considering different α, the density change of the risk state subject I in the six networks
图7. 考虑不同α时,六个网络中风险状态主体I的密度变化情况
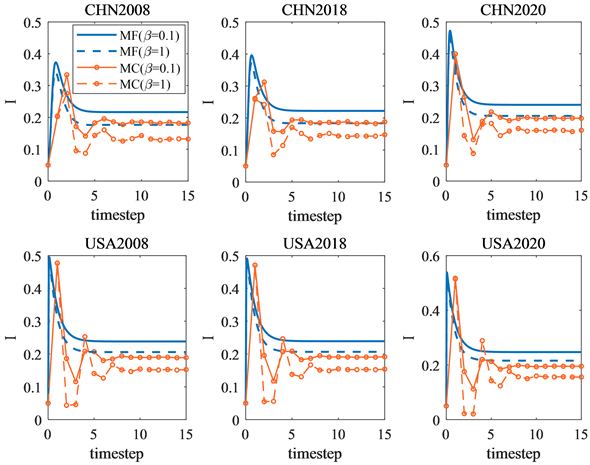
Figure 8. Considering the different rescue rates β, the change in the density of the risk state subject I in the six networks
图8. 考虑不同救助率β时,六个网络中风险状态主体I的密度变化情况
图9为考虑不同
时,各个网络中风险状态主体I密度随时间的变化曲线。当
、
、
、
,沪深市场和美股市场的
分别取0.1和0.05,
分别取0.5、1,
越大I密度越大,这是因为
代表的是移出主体变为正常主体的比例,也就是更多比例的移出状态主体不具备抵御风险的能力了,而是又进入到网络中变成其他状态的主体。
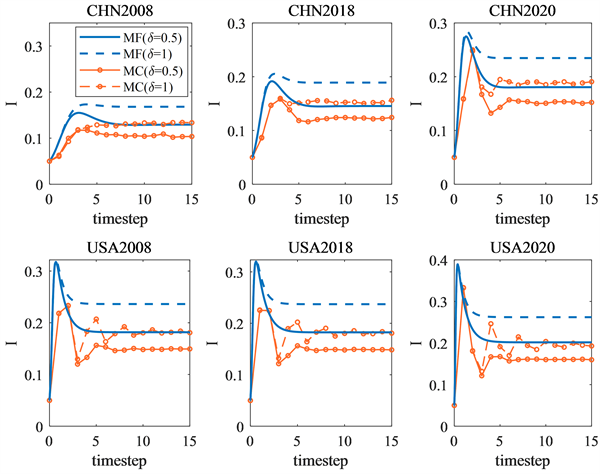
Figure 9. Considering different δ, the density change of the risk state subject I in the six networks
图9. 考虑不同δ时,六个网络中风险状态主体I的密度变化情况
5. 总结
本文将传播动力学理论与复杂网络理论相结合并引入到金融风险传播的研究中,基于传染病扩散与风险传播的相似性,研究了救助因素下的风险扩散,然后基于真实数据构建出网络,并选取合理的参数,通过模拟仿真来分析金融风险传播在不同网络中的演化过程。
美股市场的金融机构个数远远多于沪深市场,网络平均度也较大,网络整体的凝聚性都比较高。无论是美股市场还是沪深市场,关联程度高的金融机构其个数也多,如此密切的联系也增加了金融风险的传播渠道,提高了金融风险的传播程度。另外,在模拟仿真的过程中也发现,美股市场的金融网络即使是很小的传播阈值也能导致金融风险的传播,而我国的沪深市场能具备较强的风险抵御能力。在相同参数的条件下,沪深市场的金融网络能够在较短的时间内分散风险,快速到达无风险状态,这在一定程度上能够反映我国金融市场所具备的优势,能够极大地减少风险所带来的损失。
金融网络的结构会对金融风险传播产生一定的影响,网络的紧密程度越高,使得金融风险传播程度越高。模型的参数也会直接影响风险传播的情况,并决定金融网络最终的稳定水平。对于文中基于真实数据生成的六个相关网络,救助率越大风险状态主体的密度越小,外部的政策引导和救助能够有效抑制风险的扩散,更加能够说明政府的干预对金融市场所带来的积极作用,政府层面的宏观政策对于金融风险的防范和化解至关重要。另外,金融机构自身在经历过风险之后所积累的经验对于下次抵御风险也有明显的积极作用。
基金项目
2020年上海高校青年教师培养资助计划一般推荐(ZZslg20010)。