1. 引言
随着互联网普及率的提高,电子交易比重日渐提升,然而在技术进步带来电商交易繁荣的背后,欺诈交易也以惊人的速度在增长 [1]。近年来数据挖掘和机器学习的逐步发展,许多智能机器学习模型被应用在欺诈检测领域。在现有的研究中,一些基于神经网络的算法具有识别率高、鲁棒性好、施展性强的特点得到了广泛应用 [2] [3] [4] [5] [6]。以决策树模型为基础的随机森林模型也以其性能好、泛化性强、实现简单、可以应对数据不均衡等优点被给予极大关注 [7] [8] [9] [10] [11]。除此之外,许多利用技术组合或安全策略等方法进行欺诈检测的研究也给予启发 [12] [13] [14]。
在算法落地过程中,对交易金额越大的交易样本的误判往往会造成更大的经济损失,也就是说,模型对“交易金额”这一特征更加敏感。例如,一笔流水为1万元的交易与流水为100元的交易,理应受到不同程度的重视。那些大金额的交易数据才应该是模型关注的重点。然而在现有的研究中,往往忽略了交易数据的特征敏感问题,导致模型可能取得了不错的性能检测指标,但是错判的都是交易金额相对较大的样本,使得经济损失反而上升,这给欺诈检测算法的落地带来了重大隐患。
本文针对上述问题提出了一种基于特征敏感的stacking学习方法FSBS (feature-sensitive based stacking)。具体来说,首先选择五种不同质的基础分类模型,分别对训练样本进行预测,同时采用5折交叉验证的形式来避免过拟合;之后将上一步的五个结果,拼接上各个样本的真实label带入新的基于特征敏感的逻辑斯蒂回归进行训练,最终再预测的结果就是FSBS的最终结果。本篇文章的主要工作可以总结为:1) 文章提出了一种基于特征敏感学习的stacking集成方法FSBS;2) 在数据集上进行对比实验,实验结果表明FSBS相比其他方法,其错判样本的平均交易金额更小,在降低欺诈经济损失这一目的上效果更加显著。
后续文章的组织结构如下:第2节详细介绍了FSBS算法模型。第3节介绍对比实验及结果分析。第4节为结论部分。
2. 算法模型
该模型运用了集成学习模型融合stacking结合策略,它利用原始数据集训练第一层的五个初级学习器(也称为基学习器),以获得五个不同的预测结果;然后第一层得到的预测结果被最后一层基于特征敏感的次级学习器作为输入特征进行训练,得到最终预测结果,从而提高模型的准确度,减少泛化误差,并使得模型对交易金额有一定敏感度。FSBS的结构如图1所示。
2.1. 第一层模型
对于输入进模型的原始数据来说,可能是杂乱无规律的。在stacking中,通过第一层学习器后,有效的特征被学习出来了。从这个角度看,stacking第一层就是特征抽取的过程。在 [15] 的研究中,图2上排是未经stacking的数据,下排是经过stacking (多个无监督学习算法)处理后的,我们可以显著的发现红色和蓝色的数据在下排的分界更为明显。*数据经过了压缩处理,这说明有效的stacking可以对原始数据中的特征有效的抽取。

Figure 2. Data distribution before and after stacking
图2. Stacking前后数据分布
Stacking中的第一层可以等价于神经网络中的前n − 1层,而stacking中的最终分类层可以类比于神经网络中最后的输出层。不同点在于,stacking中不同的分类器通过异质来体现对于不同特征的表示,神经网络是从同质到异质的过程且有分布式表示的特点(distributed representation)。Stacking中应该也有分布式的特点,主要表现在多个分类器的结果并非完全不同,而有很大程度的相同之处。多个分类器应该尽量在保证效果好的同时尽量不同,stacking集成学习框架的对于基分类器的两个要求:① 差异化(diversity)要大;② 准确性(accuracy)要高。
因此从理论上讲,基学习器应该尽量做到“好而不同”,stacking中各个初级学习器的学习能力越强、关联程度越低,模型预测效果就越好。由于随机森林、支持向量机和梯度提升树算法在之前的研究中虽然在某些条件下有一定的缺陷,但是仍是具有较好的性能,比如随机森林和支持向量机能较好地解决小样本情况下分类器过拟合数据的问题;人工神经网络具有强大的学习能力,善于挖掘控制因素和结果之间的非线性关系等。根据理论分析和实验结果,最终的模型结构的第一层基学习器包含以下五种模型:
① 随机森林(random forest)
② K近邻(KNN)
③ 贝叶斯分类器(Bayes)
④ 多层感知机(MLP)
⑤ 梯度提升算法(Gradient Boosting Machine)
2.2. 第二层模型
在stacking分类模型中,我们在最后一层分类器使用了本文创新性提出的基于特征敏感的损失函数,它是一种基于逻辑回归(Logistic Regression)交叉熵损失函数的变种,逻辑回归是一种非常经典的分类模型,被广泛的应用于二分类的机器学习问题上。本文提出的最终损失函数
其具体形式定义如下:
其中,
为机器学习模型总的函数表达,
为在分类问题中的损失函数,常见的比如负对数似然损失、交叉熵损失、或者指数损失,
为在标准分类问题的损失函数上、按照实际情况添加的某种约束或偏重,使得最终的代价朝向一个特定的方向偏置,而这个偏置就是具体业务场景更加关注的部分;在本文FSBS模型中,
为标准的交叉熵损失函数,
为根据交易金额对样本额外添加的权重项。α为超参数。为惩罚项,γ为正则化参数,用于对参数进行约束;θ表示所有可学习的模型参数,用于L1/L2惩罚来防止过拟合。
和
表达式如下所示:
其中m为样本数量,xi为训练数据集的特征,yi为训练数据集的标签,α,K为超参数,
为训练数据集第i条交易数据的交易金额trade_amount;α越高,则损失函数中金额较大的交易数据权重就越大;K越小,就越大,模型就对金额大的数据更加敏感,最终结果就越趋向于将这些大金额样本预测正确。hθ(x)为sigmoid函数:
最终,FSBS的算法流程如下:
算法3.1:FSBS算法流程
输入:数据集
,
,
是一个d维的特征向量,
是一个一维的标签;
过程:
第一步:训练初级分类器
1:for
do
2:
3:end for
第二步:使用训练出来的初级分类器来得到预测结果,并作为数据集训练基于特征敏感的逻辑斯蒂分类器
4:
5:for
do
6: for
do
7:
;
8: end for
9:
;
10: end for
11: 以梯度
更新
的参数
12:return
输出:一组初级学习算法
基于特征敏感的逻辑斯蒂回归(次级学习算法)
3. 实验
3.1. 数据集
为了验证上述算法的有效性,本节在已有数据集上进行了对比实验验证,其中数据集的具体信息如下:本实验采用的数据集大小为5,125,107条,其中欺诈样本的有147,829条,正常样本有4,977,278条,数据维度为10维。样本的标签分布比例和交易金额分布比例如图3和图4。
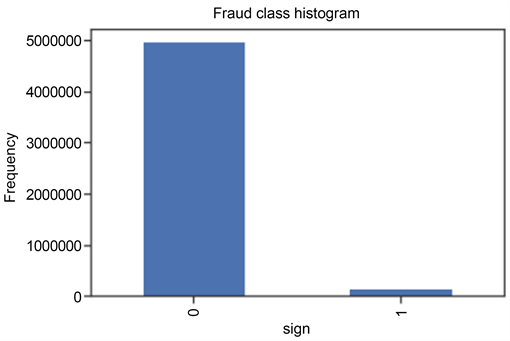
Figure 3. Proportion of sample label distribution
图3. 样本标签分布比例
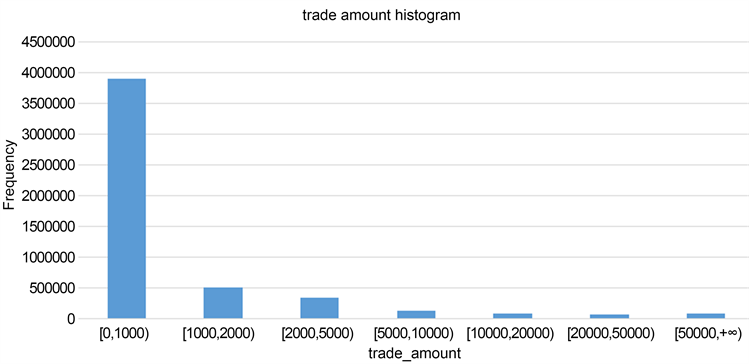
Figure 4. Proportion of sample amount distribution
图4. 样本金额分布比例
3.2. 数据指标
在本实验中,主要依据基于混淆矩阵的精准率、召回率、f1值和loss值这四个指标来衡量算法性能。对于二分类问题来说,将少数类的欺诈样本看作正样本,多数类看作负样本。混淆矩阵如表1所示:
Precision为精准率,表示实际为正例且预测为正例的样本数量在所有预测为正例的样本中的比例。Precision = TP/(TP + FP)。
Recall为召回率,表示实际为正例且预测为正例的样本数量在所有正例样本中的比例。Recall = TP/(TP + FN)。
f1值主要应用于二分类,其计算方式为:f1 = (1 + β2) * Precision * Recall/β2 * (Precision + Recall)。在本实验中β取1,表示精准率和召回率的调和平均。
Loss值表示模型错判样本的平均交易金额(单位:元)。
3.3. 实验过程
在实验过程中,模型选择和训练过程均采用第二节所述的基于特征敏感的stacking模型FSBS。在训练阶段,由于次级的训练集是利用初级学习器产生的,如果直接将初级学习器的训练结果作为次级学习器的训练集,则过拟合风险较大;因此,在每一个基础模型中应用了5倍的交叉验证。在训练过程中,从全部数据集中抽样采用70%的数据作为训练数据,30%的数据作为测试数据以调整超参数大小。在训练数据集dataset中,将其中的50%用做训练第一层分类器,其余的50%用做训练第二份分类器。具体过程如下:
① 把训练集随机分为5个相同数量的子数据集,每个子数据集不能重叠。
② 对于单个模型,4个子数据集依次作为训练集,其余的子数据集作为预测集,每个模型都可以输出自己预测集的预测结果。
③ 在上述建立的5个模型过程中,每个模型分别对测试数据集进行预测,并最终保留5列结果,然后对这5列取平均值,作为第1个基模型对训练数据的一个Stacking转换。
④ 选择第2个初级学习器,重复以上①~③操作,再次得到训练整个数据集在第2个基模型的一个Stacking转换。
⑤ 以此类推,有几个初级学习器,就会对整个训练数据集生成几列新的特征表达,同样,也会对测试集有几列新的特征表达。
⑥ 使用本文提出的基于特征敏感的逻辑斯蒂回归作为第二层的模型进行建模,分类预测。
整个分类训练过程如图5所示。
3.4. 实验结果
首先,选择几种常见的欺诈检测模型进行实验,其结果如表2;之后,按照上文所述的FSBS模型进行训练,在使用5折交叉验证对第一层分类器进行处理后,根据经验以及训练结果不断对第二层分类器的α和K这两个超参数进行调整,最终实验结果如表3。从实验结果的对比中可以看出:在泛化性上,本文提出的FSBS分类模型在f1值上与已被证实拥有良好性能的模型不分上下;在针对性上,FSBS模型的平均loss值更低,说明FSBS对大金额的交易样本更加敏感,从而在减少金融领域欺诈检测经济损失的效果上更加明显。并且,调整α和K这两个超参数还可以改变模型对金额的敏感度,当α取0时,第二层分类器退化成普通的逻辑斯蒂回归。

Table 2. Results of common models
表2. 常见模型实验结果
4. 结论
在实际金融欺诈检测的过程中,对交易金额越大的样本的误判往往会带来更大的经济损失,但目前针对整体数据样本检测性能提升的方法,并不能保证这些样本的有效识别。因此本课题在现有欺诈检测方法的基础上,进一步关注特征敏感的数据样本的有效检测。通过改进集成学习stacking集成策略,修改模型第二层的损失函数,提出基于特征敏感的stacking分类方法FSBS,以达到提升特殊样本判别准确率的目的。并最终通过实验证明,FSBS可以在保证模型泛化性的基础上,有效降低信用卡欺诈交易的经济损失。