基于ARIMA模型的云南省短期CPI预测

The Short-Term CPI Forecast of Yunnan Province Based on ARIMA Model

摘要: 居民消费价格指数(CPI)是反映居民生活中消费品和服务价格变动情况的宏观经济指标。本文选取云南省2010年1月至2021年7月的月度CPI数据建立模型，对云南省未来12个月的CPI进行预测，并提出相关建议ARIMA(1,1,0)(2,0,0)₁₂，为云南省政府有关部门制定政策提供支持。

Abstract: The Consumer Price Index (CPI) is a macroeconomic indicator that reflects the changes in the prices of consumer goods and services in the lives of residents. This paper selects the monthly CPI data of Yunnan Province from January 2010 to July 2021 to establish ARIMA(1,1,0)(2,0,0)₁₂ model, predicts the CPI of Yunnan Province in the next 12 months, and puts forward relevant suggestions to provide support for relevant departments of the Yunnan Provincial Government to formulate policies.

1. 引言

2020年新冠疫情蔓延使世界经济遭受重创，中国经济也面临严峻考验，物价水平大幅下跌，然而猪瘟盛行让猪肉价格猛涨，带动国内消费价格指数持续上涨。目前，世界经济慢慢复苏，大宗商品价格持续高涨，在如此复杂的经济环境中，CPI作为通货膨胀的重要指标，研究CPI并对其进行预测很有必要。

改革开放之后，云南省的经济得到快速发展，根据云南统计局公布的数据，近十年云南省月度CPI都保持稳定，在2020年2月CPI达到近年小高峰106.3，但在疫情之后，云南省的月度CPI波动下跌。如今云南省经济已经慢慢走向复苏，本文通过历史数据对云南省消费价格指数建立ARIMA模型，以预测未来一段时间云南省的CPI状况，为云南省政府制定宏观经济政策提供相关参考和依据。

2. 文献综述

在对CPI的预测研究文献中，学者一般采用ARIMA模型、马尔科夫链模型、灰色模型对CPI进行预测。根据研究的方法不同，可以通过以下几种模型对CPI展开预测研究。

2.1. ARIMA模型

ARIMA模型的基本思路是首先对原始数据进行平稳性和纯随机性检验，若序列不平稳先差分，后检验差分序列是否为白噪声，若为平稳非白噪声序列则拟合模型，然后对模型进行检验并展开预测。杨颖梅(2015)以北京市1998年1月至2013年5月的CPI月度数据为训练集，建立自回归单整移动平均模型ARIMA(12, 1, 8)，成功预测未来北京市7期的CPI月度数据 [1]。孙晓丹(2021)同样建立ARIMA(13, 0, 0)模型对我国CPI月度数据进行分析并预测2021年我国通货膨胀情况，研究结果表明CPI指数具有较长的滞后期，当经济复苏后，CPI指数持续回升使得通货膨胀水平稳定增长 [2]。

2.2. 马尔科夫链模型

部分学者采用马尔科夫链模型对CPI进行预测。关李娜(2021)将河北省CPI数据依据CPI与通货膨胀的关系划分为四个区间，分别为通货紧缩、正常、通货膨胀、严重通货膨胀，并以此建立马尔科夫链模型预测河北省2020和2021年的通货膨胀都为正常水平 [3]。赵雪妍(2021)利用马尔科夫模型对陕西省1998~2019年CPI数据进行分析，建立的预测模型通过了Markov检验并表明预测结果的误差控制在合理范围内，实验结果显示陕西省2021年CPI增速将保持稳定，可能在[0%, 1%)之间 [4]。

2.3. 灰色预测模型

张徐荣和袁之焕(2018)采用灰色预测模型(1, 1)对我国2011~2015年的CPI变动趋势进行预测，结果显示灰色预测相对误差小，模拟精度高 [5]。张洋洋等(2020)基于5个月的数据将改进的GM(1, 1)模型用于山东省的CPI预测中，预测精度为I级 [6]。

2.4. 文献评述

综上所述，灰色预测模型操作简单，不需要很多的样本数据就能得到精度较高的预测模型，特别是对具有短期相关性的数据效果更好。但是马尔科夫链模型的应用需要满足以下三个条件，系统状态转移概率矩阵不变；预测期内系统状态总数不变；状态转移只与时间间隔有关，只有通过检验的数据才能应用马尔科夫链模型。大部分模型基于年度历史数据对CPI进行预测，本文采用云南省月度CPI历史数据，且ARIMA模型结构简单，并不需要其他外生变量就能对CPI做出较好的拟合。因此，本文采用季节性ARIMA模型对云南省的月度消费价格指数建立模型并作出预测。

3. 理论模型

3.1. SARIMA模型介绍

在实践中，有些时间序列除了表现出普通的非平稳性以外，在周期上也表现出季节性非平稳性，可以对非季节性部分建立普通的 $\text{ARMA}\left(p,d,q\right)$，而对季节性部分建立 $\text{ARMA}\left(P,D,Q\right)$，更为一般的模型如下：

$\varphi \left(L\right){\varphi }_s\left(L^s\right)\left(L^s\right){\left(1-L\right)}^d{\left(1-L^s\right)}^D{X}_t=\Theta \left(L\right){\Theta }_s\left(L^s\right){\epsilon }_t$

这就是所谓的 $\text{ARIMA}\left(p,d,q\right){\left(P,D,Q\right)}_s$ 模型，其中有

${\varphi }_s\left(L^s\right)=1-{\phi }_1{L}^s-{\phi }_2{L}^{2s}-\cdots -{\phi }_p{L}^{Ps}$

${\Theta }_s(L^s)=1+{\vartheta }_1{L}^s+{\vartheta }_2{L}^{2s}+\cdots +{\vartheta }_Q{L}^{Qs}$

分别对应季节性的AR(P)和MA(Q)部分。

$\varphi \left(L\right)=1-{\phi }_{1}L-{\phi }_2{L}^2-\cdots -{\phi }_p{L}^p$

$\Theta \left(L\right)=1+{\vartheta }_{1}L+{\vartheta }_2{L}^2+\cdots +{\vartheta }_Q{L}^q$

分别对应非季节性的ar(p)和ma(q)。

3.2. 平稳性检验

对序列的平稳性检验一般有两种方法，一是根据图像直接作出判断，但是该方法容易主观臆测；二是通过构造统计量进行假设检验，常用ADF检验。ADF检验原理如下：

对任一AR(p)过程，有

$x_t={\varphi }_1{x}_{t-1}+\cdots +{\varphi }_p{x}_{t-p}+{\epsilon }_t$

等价变换为：

$x_t-x_{t-1}={\varphi }_1{x}_{t-1}+\cdots +{\varphi }_p{x}_{t-p}+{\epsilon }_t$

整理上式为：

$\nabla x_t=\left({\varphi }_1+\cdots +{\varphi }_p-1\right)x_{t-1}-\left({\varphi }_2+\cdots +{\varphi }_p\right)\nabla x_{t-1}-\cdots -{\varphi }_{p-1}\nabla x_{t-p+1}+{\epsilon }_t$

简记为：

$\nabla x_t=\rho x_{t-1}+{\beta }_1\nabla x_{t-1}+\cdots +{\beta }_{p-1}\nabla x_{t-p+1}+{\epsilon }_t$

其中：

$\rho ={\varphi }_1+{\varphi }_2+\cdots +{\varphi }_p-1$

${\beta }_j=-{\varphi }_{j+1}-{\varphi }_{j+2}-\cdots -{\varphi }_p,j=1,2,\cdots ,p-1$

若序列 $\left\{x_t\right\}$ 平稳，则

${\varphi }_1+{\varphi }_2+\cdots +{\varphi }_p<1$

等价于 $\rho <0$。

若序列非平稳，则至少存在一个单位根，有

${\varphi }_1+{\varphi }_2+\cdots +{\varphi }_p=1$

等价于 $\rho =0$。在AR(p)过程单位根检验的假设条件可以确定为：

${\text{H}}_0:\rho =0$

${\text{H}}_1:\rho <0$

构造ADF检验量：

$\tau =\hat{\rho }/s(\; \rho \; ^\; )$

其中 $s\left(\hat{\rho }\right)$ 为参数 $\rho$ 的样本标准差。

3.3. 纯随机性检验

模型的显著性检验一般通过对序列残差进行白噪声检验 [7]。

原假设：

${\text{H}}_0:{\rho }_1={\rho }_2=\cdots ={\rho }_p=0,\forall m>1$

备择假设：

${\text{H}}_1:至少存在某个{\rho }_k\ne 0,k<m$

LB统计量由Ljung和Box证明出其近似服从自由度为m的卡方分布，数学表达式为：

$\text{LB}=n\left(n+2\right){\displaystyle \underset{k=0}{\overset{m}{\sum }}\left({\hat{\rho }}_k^2/n-k\right)}~X^2(\; m\; )$

其中，m为延迟期数，n为观测期数。若LB统计量小于显著性水平，认为原序列为非白噪序列，数据具有可提取的信息，可以继续拟合模型。

4. 数据来源

本文采用数据来自《云南统计年鉴》，选取云南省2010年1月至2021年7月的月度居民消费价格指数为样本数据，利用ARIMA模型进行CPI预测。

根据图1可知，近十年里云南省月度CPI的顶峰是2020年2月106.34，2014年至2018年初云南省月度居民消费价格指数波动下跌，2018年小幅上涨，后经历新冠疫情、猪肉价格上涨、经济慢慢复苏等复杂环境，让云南省的月度居民消费价格指数急剧上涨后断崖式下跌。

Figure 1. Raw data timing diagram

图1. 原始数据时序图

5. 建模分析

5.1. 数据平稳性和纯随机性检验

首先对原始时间序列进行ADF检验，检验结果见表1。在5%显著性水平下，无漂移项无趋势项模型、有漂移项无趋势项模型、有漂移项有趋势项模型均没有通过ADF检验，因此认为原始时间序列是不平稳的。

Table 1. ADF inspection of original sequence

表1. 原始序列ADF检验

将原始CPI月度数据进行一阶差分，差分之后时序图见图2。

一阶差分后的自相关图和偏自相关图见图3，都呈现出1、12阶显著，且图像近似三角函数，表明一阶差分后的序列具有季节效应。故对1阶差分后的序列再进行12步差分，然后对1阶12步差分的序列进行单位根检验，单位根检验结果如表2所示。在5%显著性水平下，三种模型的P值均小于或等于0.01，表明1阶12步差分后的云南省月度CPI数据已经实现了平稳。

Figure 2. Timing diagram after 1st order difference

图2. 一阶差分后时序图

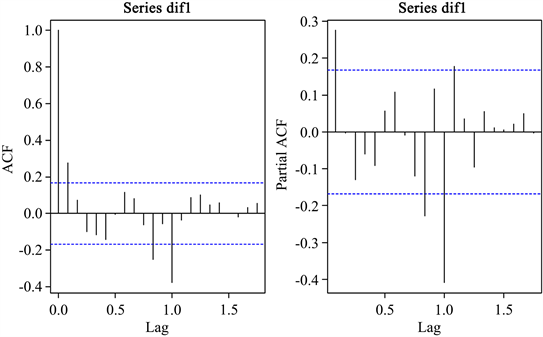
Figure 3. ACF and PACF diagrams after first-order difference

图3. 一阶差分后的ACF、PACF图

Table 2. ADF test after CPI’s first-order 12-step difference

表2. CPI的1阶12步差分后的ADF检验

数据具有平稳性质之后再通过“Ljung-Box”进行纯随机性检验，以判断平稳时间序列是否为白噪声。检验结果见表3所示。

Table 3. Pure randomness test

表3. 纯随机性检验

根据表3的纯随机性检验结果，延迟6阶和12阶的LB统计量P值均未超过显著性水平0.05，表明1阶12步差分后的云南省月度CPI数据是平稳非白噪声序列，可以用ARIMA建立模型。

5.2. 模型建立

5.2.1. auto.arima函数定阶

采用auto.arima函数对模型进行定阶，R软件自动拟合的模型为 $\text{ARIMA}\left(1,1,0\right){\left(0,0,2\right)}_{12}$，拟合结果如表4所示，3个系数中只有两个系数大于其两倍标准差，1个系数不显著。

5.2.2. 观测法定阶

1阶12步差分后的自相关图及偏自相关图见图4所示。

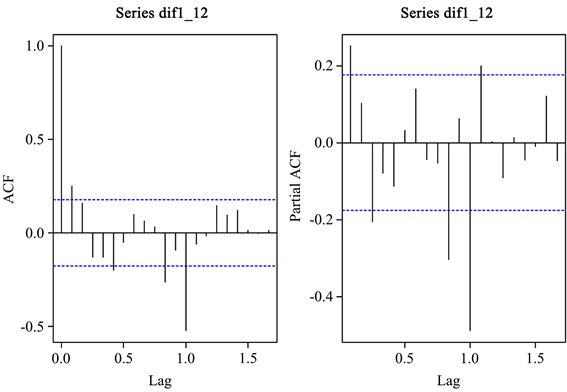
Figure 4. ACF and PACF diagrams after 1st-order 12-step difference

图4. 1阶12步差分后的ACF、PACF图

根据1阶差分及1阶12步差分的自相关图及偏自相关图，拟合模型 $\text{ARIMA}\left(1,1,0\right){\left(2,0,0\right)}_{12}$ 、 $\text{ARIMA}\left(1,1,0\right){\left(1,0,0\right)}_{12}$，模拟结果见表4所示。

Table 4. Model fitting results

表4. 模型拟合结果

$\text{ARIMA}\left(1,1,0\right){\left(2,0,0\right)}_{12}$ 模型的系数均大于两倍标准差，表明系数显著，且根据AIC准则，拟选择 $\text{ARIMA}\left(1,1,0\right){\left(2,0,0\right)}_{12}$ 模型，模型表达式为：

$\left(1-0.3294B\right)\left(1+0.6983B^{12}+0.3363B^{24}\right)\left(1-B\right)X_t={\epsilon }_t$

5.2.3. 模型检验

对 $\text{ARIMA}\left(1,1,0\right){\left(2,0,0\right)}_{12}$ 模型的残差进行检验，见图5所示，残差的白噪声检验P值全都位于显著性水平5%之上，表明模型是显著的。

Figure 5. Model significance test plot

图5. 模型显著性检验图

再通过Ljung-Box对模型显著性进行检验，检验结果见表5所示。

Table 5. Model significance LB test

表5. 模型显著性LB检验

滞后6阶的P值均大于显著性水平0.05，接受残差为白噪声的原假设，说明 $\text{ARIMA}\left(1,1,0\right){\left(2,0,0\right)}_{12}$ 模型显著。

5.2.4. 模型预测

本文以2010年1月至2021年7月的云南省月度CPI指数为实验集，建立 $\text{ARIMA}\left(1,1,0\right){\left(2,0,0\right)}_{12}$ 模型，预测云南省未来12期的月度居民消费价格指数。预测效果图见图6。

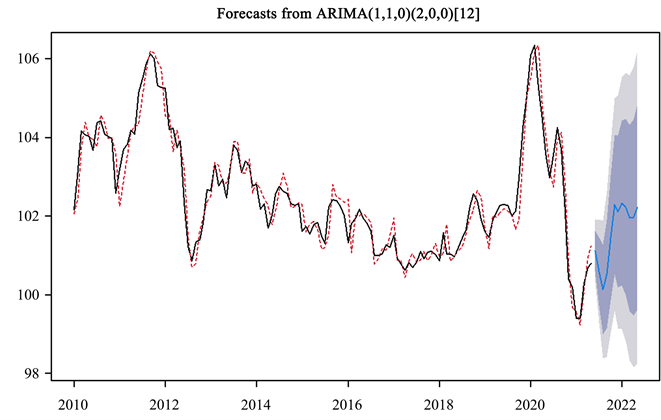
Figure 6. Model fitting and prediction renderings

图6. 模型拟合及预测的效果图

图6是模型预测效果图，虚线表示拟合值，实线表示观测值。阴影部分的实线为预测值，深色、浅色阴影分别为序列80%和95%置信区间。预测效果图显示，模型拟合值与真实值比较接近，拟合效果良好。由于ARIMA模型的预测方差会随着预测步长的增加而逐渐增大，所以ARIMA模型通常用于短期预测。

表6是模型的12期预测值，将2021年8月至12月的真实值与预测值进行对比发现，相对误差随着时间的推移逐渐增加，前5期的平均误差为4.45%，表 $\text{ARIMA}\left(1,1,0\right){\left(2,0,0\right)}_{12}$ 模型在预测云南省短期月度CPI时效果好。

Table 6. Model prediction results and real value comparison results table

表6. 模型预测结果与真实值对比结果表

6. 结论与建议

从预测结果来看， $\text{ARIMA}\left(1,1,0\right){\left(2,0,0\right)}_{12}$ 模型在短期内对云南省月度CPI的预测较为准确，可根据此模型对云南省未来的短期CPI走向作出预测。根据预测结果，未来一年时间内云南省的月度CPI将稳中有升，表明云南省的经济正从疫情中慢慢恢复过来，为避免通货膨胀降低居民生活质量损害居民利益，政府应当提前制定相应调控政策以保障物价水平正常波动，使云南省的经济发展保持稳中向好趋势。