1. 引言
安徽科技学院定位于高水平应用型本科高校。为了提升本科生对专业公式、定理的深入理解和应用水平,我校从2015年开始在机械工程各专业的专业基础课程中开始推广使用专业工程案例式教学法。该教学法经过课堂工程案例的讨论、提出问题、介绍并引入解决问题所需要的基础知识、解决问题、总结引申5个教学步骤,使学生能够更加深刻地理解所学基础课程知识的专业用途以及用法,在这个过程中相对弱化公式定理的理论推导,实际上体现了一种由特殊到一般的知识建构过程,更加符合应用型本科高校的办学特点和学生的数理基础特点 [1] [2] [3] [4]。工程案例教学可以极大提高学生们学习基础力学的兴趣。通过工程案例教学,学生们可以真实、具体地感受到课堂知识对他们专业的重要性,激起学习的兴趣,变被动学习为主动学习。以下是机械工程专业《材料力学》叠加原理教学中的一个工程案例。
叠加原理是机械工程各专业《材料力学》课程中的一个重要定理。该定理的核心含义是说多个载荷综合作用下塑形金属材料线弹性变形范围内的内力、应力、变形、应变等物理量,等于这些载荷分别单独作用在该金属材料上所产生的内力、应力、变形、应变的叠加。在课程组受蚌埠市行星工程机械有限公司委托为其开发的树状立体停车库的立柱尺寸设计中 [5] [6] [7] [8] [9],就重点采用了《材料力学》中的叠加原理 [10]。课题组总结了立柱的设计过程,最终形成了用于《材料力学》叠加原理讲解的工程案例,并应用到了本科生课堂讲解中,取得了良好的教学效果。
2. 课堂工程案例的讨论
以课题组研发的树状立体停车库为教学案例,来引入《材料力学》在实际中的应用。课程组负责人曾经受蚌埠市行星工程机械有限公司委托,设计研发一种树状立体停车库。该车库要求在占地不超过2 m2的前提下停放不少于6辆2 t以下的汽车。课题组最终确定的树状立体停车库设计方案如图1所示,立柱占地面积只有1.8 m2。

Figure 1. Design scheme of tree-shaped three-dimensional parking garage
图1. 树状立体停车库设计方案
3. 提出问题
立柱一侧停满车辆另一侧空置,即一侧偏载时对立柱产生的侧向弯矩最大,工况相对最恶劣,其力学模型如图2所示。在模型中测出车辆和载车板放在一起的重心离立柱的中性轴的距离为1900 mm,两者总重量3000 kg,故每一层偏心载荷对立柱产生的弯矩Me为
(1)
依据GB 1589-2016《汽车、挂车及汽车列车外廓尺寸、轴荷及质量限值》4.1.1.2 [3] 中一般汽车车高限值2200 mm,所以每层之间的间隔方案定为f = 2200 mm。三层立柱总的高度H为8500 mm。在此工况下以及多个弯矩的综合作用下载荷下,立柱的尺寸该如何设计呢?
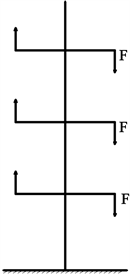
Figure 2. Simplified model of the eccentric load of the column
图2. 立柱偏心载荷受力简化模型
4. 介绍并引入解决问题所需要的叠加原理
根据前面几步的引导,引入叠加原理:塑形材料变形在多个载荷综合作用下如果其变形始终处于线弹性范围内,那么材料的内力、应力、变形、应变等物理量,等于这些载荷分别单独作用在该金属材料上所产生的内力、应力、变形、应变的叠加。比如梁在多种载荷作用下产生的挠度
、转角
以及应力
就分别可以按照如下公式表述
(2)
(3)
(4)
5. 用叠加原理解决问题
立柱结构受载模型是一个悬臂梁,在梁的不同位置承受了3个弯矩。按照叠加原理的解释,梁在三个弯矩综合作用下的转角和挠度等于这三个弯矩分别单独作用下悬臂梁上时所产生的转角和挠度的叠加。根据《材料力学》中的挠曲线方程可以计算出立柱在极限偏载情况下顶端的挠度位移量
(5)
L为悬臂梁长度;I为立柱截面惯性矩。
立柱顶部端截面转角
(6)
每一个弯矩都是由车辆和载车板的自重引起且是相等的,分别记为M1、M2、M3。每一个弯矩对立柱顶部产生的挠度位移记为
。每一层端部倾斜角所造成的剩余部分立柱的端部所产生的挠度位移记为
。每一个力矩所引起的立柱顶端的倾斜角记为
。从地面开始每去掉一层后立柱余下的部分称为剩余长度Li,其中i为去掉的层数。
(7)
立柱顶部最大挠度为
(8)
各截面倾斜角为
(9)
转角引起的挠度为
(10)
叠加法求得端部的总挠度为
(11)
该车库起重形式类似于塔式起重机,《起重机设计规范》(GB/T 3811-2008) 5.5.2.2 [4] 规范塔式起重机其端部的水平静位移值应不大于结构总高度的1.34%,即
(12)
槽钢平面图惯性矩如下式所示
(13)
(14)
经计算立柱总变形位移远远小于规范限定值,满足规范要求。
立柱发生压弯扭组合变形,按照叠加原理的解释,立柱上的最大应力应该等于压缩产生的应力与弯曲产生应力的叠加。立柱框架结构同时考虑轴向力即立柱自重和载车板及其上的车辆两者总重FN引起的轴向应力以及弯矩Mmax的弯曲正应力的影响,可以得出立柱危险部位为四根主支撑根部,最大应力容易发生在此位置,对立柱后侧矩形管进行强度校核,计算如下:
(15)
计算应力结果立柱底部最大应力为63.06 MPa小于156.67 MPa的许用应力值,符合强度安全要求。
6. 总结与引申
通过立体停车树立柱的设计与校核问题,深刻阐明了叠加原理的具体用途与用法。同学们举一反三,通过知识迁移,所有零部件在多种载荷作用下所产生的强度以及刚度问题都可以采用叠加原理来解决。从这一点上来说,叠加原理在机械工程中的强度与刚度问题中具有普适性,需要大家用心掌握。
基金项目
安徽省质量工程项目项目(2019jyxm0318;2019jxtd084;2017mooc108)。
NOTES
*通讯作者。