1. 引言
近年来,我国酒店行业发展势头强劲,主要归功于酒店行业自身的服务能力不断提高以及旅游业的蓬勃发展,从而推动了酒店行业市场需求不断扩大 [1]。网络时代,公开的酒店评分成为大众选择酒店的重要参考依据,提升评分对于吸纳顾客具有重要的意义 [2]。本文对比不同星级的酒店评分的显著影响因素及在酒店服务、酒店规模、酒店口碑等方面的区别,分析宁波市酒店行业的发展现状。
通过大数据共享交易市场iDataAPI平台获取综合排名为前六百的酒店数据并进行汇总。包括酒店平均价格、品牌名称、早餐信息、经营状况、评论数、地区、环境评级、收藏数、是否提供WIFI、酒店类型、质量等级、评分、客房数、星级等信息。通过多元回归分析及因子分析等统计分析方法对宁波不同星级的酒店间的规模、服务、口碑等方面进行实证分析。
2. 多元回归模型实证分析
2.1. 多元回归分析意义
初步通过描述性分析得出不同星级的酒店对于该酒店的评分具有较大差异,但不同星级是较为抽象的概念,为深入分析不同星级的酒店之间的具体差异,建立多元回归模型,进一步分析对酒店评分显著的因素。
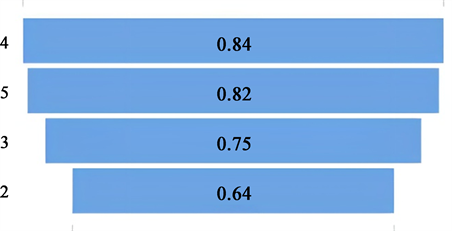
Figure 1. Display of average value of different star ratings
图1. 不同星级评分平均值展示
由图1得,大数据共享交易市场iDataAPI平台获取综合排名为前六百的酒店不同星级评分平均值展示,纵坐标数字代表酒店星级数。从中发现随着星级的增加,酒店的总体评分也随之增加,但各个星级之间的差距并不是很大,尤其是四星级与五星级酒店,甚至四星级酒店的平均得分高于五星级酒店。因评分为酒店平台所给标准,并不清楚其实际的评分规则,可通过多元回归分析后,初步探索评分标准,以便进一步分析对酒店评分显著的因素。
2.2. 模型建立的思路
选择评论数、平均价格、星级、质量等级、是否提供WiFi、环境评级、优质评论数、收藏数、总共层数和客房数这十个变量作为自变量,酒店的评分作为因变量初步建立回归模型;进行显著性检验,剔除未通过显著性检验的变量;进行正态性检验所有变量是否或近似符合正态性,通过逐步回归调整变量,优化模型的拟合度。
2.3. 实证分析
通过观察选出大致可以用作评分的变量,分别是评论数、平均价格、星级、质量等级、是否提供WiFi、环境评级、优质评论数、收藏数、总共层数和客房数这十个相关变量。

Table 1. Estimation of model parameters
表1. 模型参数估计表
通过表1可以得出,变量并没有全部通过显著性检验。最显著的变量是评论数、质量等级和环境评级。是否提供WiFi对评分有较强的影响。平均价格和客房数对评分要求会有一定的影响,但并不显著。
模型优化1:选出显著性变量,进行分析:选择评论数、平均价格、质量等级、是否提供WiFi、环境评级和客房数这六个变量对评分的影响。
模型:
(其中,
表示评分,
表示评论数,
表示平均价格,
表示质量等级,
表示是否提供WiFi,
表示环境评级,
表示客房数)。
从表2可知,删减变量之后的模型的结果显示,各因变量的P值都有所减小,模型的性能提高了,说明选择评论数、平均价格、质量等级、是否提供WiFi、环境评级和客房数这六个变量对评分都有较强的影响。

Table 2. Estimation of optimized model parameters
表2. 优化后的模型参数估计表
2.4. 正态性检验
在用线性回归模型拟合数据之前,首先要求数据应符合或近似符合正态分布,否则得到的拟合函数不正确。
对因变量进行正态性检验:

Table 3. Test table for normality of dependent variables
表3. 因变量正态性检验表
从表3可知因变量“评分”是正态性。
对自变量进行正态性检验:

Table 4. Test table for normality of independent variables
表4. 自变量正态性检验表
从表4可知所有的自变量都是正态性。
对残差进行正态性检验:

Table 5. Test table for normality of residuals
表5. 残差正态性检验表
从表5可知残差也呈现正态性。
模型优化2:通过逐步回归,进行分析:从可用变量中选择对因变量有较大影响的自变量以建立方程式,并且对因变量没有较大影响的自变量不包括在方程中。

Table 6. Stepwise regression results
表6. 逐步回归结果表
从表6的程序运行的结果可以得知,当用全部变量作回归时,AIC值最小。接下来显示的数据说明,如果分别去掉其中一个自变量,AIC值都会发生变化,但是所有变化的AIC的值都大于原先全部变量回归时的AIC值。
分析一下计算结果,提取相关信息:

Table 7. Parameter estimation after stepwise regression
表7. 逐步回归后参数估计表
从表7的运行结果来看,回归系数的检验的显著性水平变化不大,说明所选择的自变量都是具有较强的显著性。把全部变量作回归时,不仅AIC值最小,残差的平方和也是最小。拟合越好的方程,残差的平方和越小。模型的R方值为0.4023,相比于之前的模型提高了。
逐步回归后的模型:
(其中,
表示评分,
表示评论数,
表示平均价格,
表示质量等级,
表示是否提供WiFi,
表示环境评级,
表示客房数)。
3. 因子分析实证分析
3.1. 因子分析意义
因子分析是将多个实测变量转换成少数及格综合指标,体现的也是一种降维思想。通过降维将相关性高的变量聚类在一块,从而减少待分析变量的数量,进而减少问题分析的复杂程度 [3]。
3.2 实证分析
1) 确定因子个数
图2中横坐标表示因子数,纵坐标表示特征值。图2为帮助我们确定主成分合适个数的视觉工具,将特征值从大到小排序,选取一个拐点对应的序号,若此序号后的特征值全部较小且彼此大小差异不大,这样选取的序号作为主成分个数,依据上述图利用决定提取三个主成分。
2) 计算因子成分与贡献率
选择三个主因子,第一公共因子为酒店规模管理,第二公共因子为酒店服务管理,第三公共因子为酒店口碑管理。如下图3所示:
因子贡献及贡献率如表8所示:
由表8可以看出选择3个主成分达到81%的累计贡献率,能够提取到数据中的有效信息,其他主成分部分之间的贡献率较小且差异不大,可选择舍弃,因子载荷矩阵表见表9。
3) 计算因子得分
计算因子得分,并进行总得分综合。
用回归方法求各个因子得分函数:
记每个样本点对因子
综合得分的估计值为:
。
利用计算所得各因子指标与综合得分指标结果作图展示如下图:
图4为酒店星级与各因子得分平均值的交叉分析,由上图可以看出,只有在酒店规模管理方面呈现明显上升趋势,而在服务管理方面与口碑方面并没有明显的区分,由此可以看出根据星级判定只是酒店规模方面有明显的区分,而并没有对酒店进行综合性区分,通过对酒店根据各因子指标与综合指标进行聚类分析显示酒店被明显区分为3类,且并无模棱两可的酒店类型,区分良好,以下根据上述聚类类别对酒店各因子指标与星级进行分析:
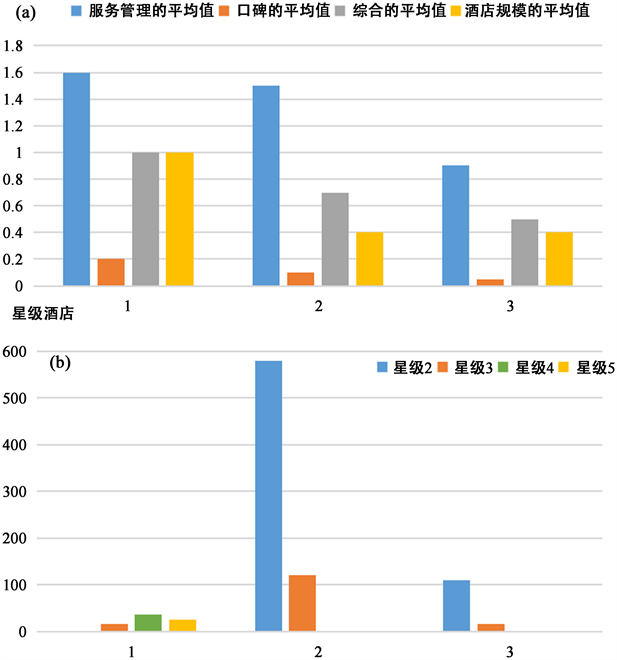
Figure 5. Relationship between stars, categories and factors
图5. 星级、类别和因子关系图
图5(a)为酒店聚类类别与各因子指标之间的关系,可以看出,类型1不管从酒店服务管理方面、口碑方面、酒店规模方面还是总体综合方面都表现最优秀,而类别2的酒店次之,类别3的酒店最差。
图5(b)可以看出一个有趣的现象,类别1中包含少部分三星级酒店和所有四星级、五星级酒店,说明此类酒店确实是不论从服务方面、口碑方面还是酒店规模方面都表现突出。而类别2中包含大部分二星级酒店与部分三星级酒店,从服务管理、口碑与酒店规模方面都表现良好,且体现出目前一部分二星级酒店可以与三星级酒店媲美,除规模方面有所区别外,服务方面与口碑方面都不亚于三星级酒店,而第3类则为一部分为二星级酒店与三星级酒店,应为一部分旧型经济型酒店,配备设施等并未跟随潮流或不能表现出一定的舒适性。
4. 结论
结果显示,宁波酒店应在评论数、平均价格、质量等级、是否提供WIFI、环境评级以及客房数等方面提升,以获取较高的评分,增强自身的竞争力。
基金项目
宁波市自然科学基金(2019A610041);国家级大学生创新创业项目(202111058033)。