人工智能语义分割技术在钢琴教育中的应用研究

Application of Artificial Intelligence Semantic Segmentation Technology in Piano Education

摘要: 目前，素质教育越来越被重视，作为素质教育代表的音乐教育也越来越被关注，但是音乐教育却极大受限于人工教育资源。人工智能在音乐教育中的辅助，从计算机的角度讲就是信号类型转换的过程。例如对于学者弹琴，需要将钢琴的信号转换特定的数字信号与真实的谱子进行对比纠错，从而识别错音、错节奏的现象并实时校正。这一规范技术过程被称为自动音乐转录AMT (Automatic Music Transcription)。本文采用谐波常数Q变换、CFP等不同的音乐数字特征表示方法，将原始的音乐信号转换为频谱图，作为网络结构的特征输入，改进了语义分割模型DeepLabv3+，融合了U-Net的U型结构对多乐器音乐进行转录，该算法在钢琴音乐MPAS数据集上达到了良好的识别效果。

Abstract: At present, quality education is more and more valued, and music education as a representative of quality education is also more and more concerned. But music education is greatly limited by artificial educational resources. The help of artificial intelligence in music education is the process of signal type conversion from the perspective of computer. For example, for scholars to play piano, it is necessary to convert the piano signal to a specific digital signal and compare it with the real spectrum to correct errors, so as to identify the phenomenon of wrong sound and wrong rhythm and correct it in real time. This standardized technical process is called Automatic Music Transcription (AMT). The algorithm comprehensively makes use of digital feature representation methods such as harmonic constant Q transformation and CFP. It converts the original music signal into a spectrum chart as a feature input of the network structure. It improves semantic segmentation model DeepLabv3+ and incorporates U-Net’s U-shaped structure to transcribe multi-instrument music. The algorithm achieves good performance on piano music MPAS datasets.

1. 引言

近年来，我国素质教育中最具代表性的音乐教育越来越被社会所关注。国内教育资源尤其是专业的指导老师数量供不应求，故此广大的学者只能局限在时间有限的课堂中得到专业指导，而在多数练习时间中却得不到专业的矫正。在素质教育迅速发展的今天，数量庞大的学者需要得到更关切、更正确、更直接的辅助性指导。课上受到指导的时间由一节课的课时所限制，而在课外需要长时间、大量地练习。在练习过程中，他们需要一个强有力的“指导老师”来解决他们存在的问题，譬如错音、错节奏、弹琴指法规范性等等。目前，机器学习在声学领域取得了良好发展。

广大的学者如何能够从人工智能的辅助与监督中得到规范而严格的指导是一项很有研究意义的课题。利用人工智能来进行音乐辅助练习，其实就是将声学信号转换为数字信号后，由AI模型进行分析的过程。对于学者弹琴，需要将钢琴的信号转换成特定的数字信号格式与真实的谱子进行对比纠错，从而识别错音、错节奏的现象并实时校正。这一规范技术过程被称为自动音乐转录(Automatic Music Transcription, ATM)或自动演奏识别。作为音乐信息检索中的基本问题，ATM能够为哼唱识别，乐曲匹配提供有力的技术支撑。ATM包括F0检测 [1]、多音级估计、音符起止点检测等。

在单音音乐转录中，机器学习在音高识别方向取得了重大突破。但是对于多音音乐转录中的音高识别和乐器匹配问题，仍在研究探索阶段。本文的研究重点就是乐器中音高识别和匹配问题。

2. 基于语义分割网络的自动音乐转录方法

2.1. 方法概述

本文提出的模型如图1所示。

语义分割网络模型首先将输入的原始音频数据经过数字信号处理变换为频谱图，组合频谱图(CFP与HCQT)经过数据预处理后提取时频域信息和谐波信息。在输入数据的特征中，长宽分别代表着时域和频域维度，通道数则代表着谐波信息。网络模型基于DeepLabV3以及DeepLabV3+中提出的全卷积网络结构和编码–解码器结构(Encoder-Decoder Block)。原始的DeepLabV3只处理单一图片并进行像素密集分类，一般输出在单通道上的二分类，属于单任务模式。为了能够识别多乐器特征，本文将输出映射到N + 1个维度上，以识别N种不同类型的乐器并附带有一个乐器无关通道。因此对于前N个维度，每个维度都代表着一种乐器的转录结果。所以该模型能够同时预测多维度乐器输入。输出在每个通道上的像素值基于0到1之间，代表着当前音高在本乐器中是否活跃。

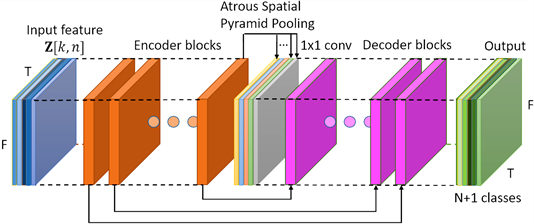
Figure 1. Semantic segmentation network model

图1. 语义分割网络模型

2.2. 音乐特征提取

音频数据需要经过预处理过程才能作为网络结构的输入。本文的数据特征表示基于文献 [2] 提出的组合频谱CFP和文献 [3] 提出的HCQT变换。文献 [2] 已经证明了时频域中的组合多特征表示方法能够有效减小谐波干扰，提高ATM的最终预测性能。此外，为了更好地捕获谐波信息，本文还借鉴了文献 [2] [3] 中提出的沿着通道维度方向叠加谐波信息的特征表示办法HCQT变换。

假设输入的音频数据经过短时傅里叶变换后得到得特征矩阵为 $X\in R^{F\ast T}$，其中F代表着频谱图中有效频率范围的频域维度，T代表着时间维度。考虑公式(1)和(2)中数据特征表示办法。

$Z_f\left[k,n\right]=Q_f{\left|W_{f}X\right|}^{{\gamma }_f}$ (1)

$Z_q\left[k,n\right]=Q_q{\left|W_q{F}^{-1}{Z}_f\right|}^{{\gamma }_q}$ (2)

其中 $Z_f$， $Z_q\in R^{F\ast T}$，k，n分别是数组中时间维度和频率维度的索引，矩阵 $F^{-1}$ 是离散傅里叶变换的逆变换矩阵， $W_f$ 和 $W_q$ 是两个高通滤波器，高通滤波器能够丢弃低变部分， $\gamma$ 是元素级的幂阶ReLu激活函数，即 ${\left|x\right|}^{\gamma }={\left|\text{ReLu}\left(x\right)\right|}^{\gamma }={\left|\max \left(0,x\right)\right|}^{\gamma }$。本文基于文献 [4] 的设定 $\left({\gamma }_f,{\gamma }_q\right)=\left(0.24,0.6\right)$ )。 $Q_f,Q_q\in R^{F\ast 2F}$ 是两个三角滤波器组，它们分别实现时域和频域到有效对数频域的特征映射。两个滤波器组都包含352个，每八度48个半音的三角滤波器，覆盖范围为27.5 Hz (A0)到4487 Hz (C8)。因此，最终的频率表示中，频域范围F = 352，时域范围T根据输入的音频长度确定。简单来讲， $Z_f$ 代表的是原始音频数据的基频和基频高次谐波的幂阶频谱图(Spectrum)，而 $Z_q$ 代表的是基频和基频低次谐波的广义倒谱图，文献中指出，对于多音级识别模型来说组合 $Z_f$ 与 $Z_q$ 能够明显地提供比频谱图更好的性能 [5] [6]。

2.3. 语义分割转录模型

模型结构如图1所示，模型具体参数见图2。输入数据特征为 $Z_{HCFP}\in R^{2m\ast F\ast T}$ 其中，2m代表着模型通道数，在HCFP中表示即是谐波分量，F和T分别代表频域和时域，本文中采用的时间步长为256，频域跨度为352。

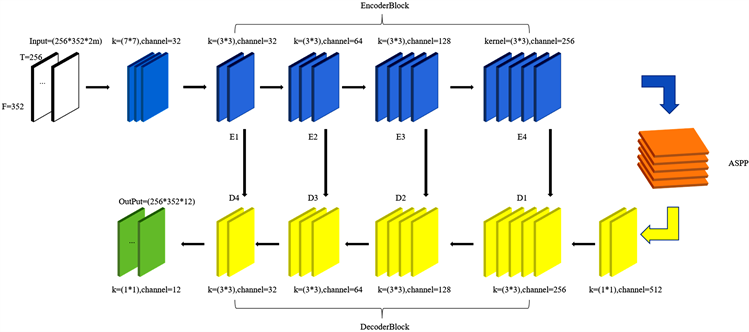
Figure 2. Semantic segmentation network model details

图2. 语义分割网络模型细节

输入特征首先经过一层尺寸为7*7的卷积层，扩展通道数到32，然后输入到编码器序列。编码器总共有四个模块E1、E2、E3和E4，每个模块都由若干层编码块组成，编码块中包含两个空洞卷积层和一个可选的跳跃全连接层 [7]，编码块的结构如图3所示。

Figure 3. Encoding block structure

图3. 编码块结构

编码块中的两层空洞卷积层使用的尺寸均为3*3，考虑音频数据中低维数据在频率和时间维度上都很敏感，即每个音符在图像中可是被视作为小物体，因此采用的膨胀率均为1。当第一个空洞卷积层的步长不为1的时候，跳跃连接层就会被激活。输入音频经过一层卷积层后featuremap变为256*352*32。进而输入到编码器E1。E1中通道数均为32，第一个编码块步长为2，跳跃连接层被激活，第二个编码块步长为1，经过E1后特征大小、维度都不变。E2中通道数均为64，第一个编码块步长为2，跳跃连接层被激活，后续编码块步长均为1，音频特征经过第二层编码块后featuremap变为256*352*64。类似地，经过E3、E4后，音频特征大小最终被编码为256*352*256。编码器提取了音乐的高纬度特征，降低了音频数据的时间和频率分辨率。

音乐特征经过编码器之后输入到ASPP结构中，用于音乐转录模型的ASPP结构如图4所示。首先经过1*1*512卷积层将音频特征升维到512，经过四层膨胀率为1，2，4，8的膨胀卷积层后并联在一起，再经过一层1*1*512的卷积层输出到解码器结构。ASPP结构消除了全连接层特征大小的限制，简化了网络结构的设计，尤其是对针对类似音乐这种长度不固定的特征。对于音乐数据当模型一步步进行下上采样过程的时候，频率分辨率也会越来越小，因此当频率分辨率过小的时候采用较大膨胀率的空洞卷积仍然能够提取原始音频数据的局部特征信息，从而更好地进行时频域分离，来达到预测不同乐器种类中，音高的识别效果。

Figure 4. ASPP structure for music transcription model

图4. 用于音乐转录模型的ASPP结构

解码器也包含四个模块D1、D2、D3和D4，每个模块都包含一个解码块。解码块与编码块结构完全一样，只不过第二个卷积被替换成为了转置卷积。经过ASPP结构处理后的音乐特征大小为256*352*512。经过一层1*1的卷积核后降维到256，然后合并编码块中E4的特征输入到D1中。D1中解码块的通道数为256，经过解码块之后并联E3的特征，经过一层大小为1*1，通道数为256的卷积层后跳跃连接解码块之前的音频特征。D2、D3和D4的结构与D1一模一样，通道数逐渐递减为128、64和32，最后再经过一层通道数为12的卷积层输出分类结果。解码器从物理意义上是对音频数据的上采样，逐层恢复音频数据的时间和频率分辨率。

编码器和解码器之间借鉴了U-Net结构，但是对像素敏感类型的音乐特征信号，在频域中一个微小的改变都会对最终音高预测的结果产生巨大影响，这是因为在变换过程中，时域到频域是经过对数变换处理了的，当从频域恢复到时域就变成了指数变化。这里的跨步连接能够将低维的高频率分辨率信息特征保留下来，输入到高纬度特征中，这样一来低维的高频率分辨率信息和多维度信息就都被保留下来了。

为了防止过拟合现象，本文模型中在卷积层之后均对数据进行了正则化处理和Dropout层，其中失活率Dropout为0.4。模型统一用ReLu激活函数。

最后模型采用焦距损失函数(Focal Loss Function) [8] 来解决最后预测中的分类不平衡的问题 [9]。由于输出的结构是稀疏矩阵，即当前时间激活的音高少而未激活的音高多，因此导致大多数像素值为0，传统的损失函数，例如二元交叉熵，模型最终将会倾向于将大部分像素值预测为0。焦距损失函数能够提供一个权重因子，用于平衡激活和未激活音符之间的比例协调性，因此焦距损失函数更有助于声乐旋律的提取 [7]。

3. 实验与分析

3.1. 实验数据集和环境

1) 实验数据集

实验采用了单钢琴乐数据集MAPS。本文中采用MAPS数据集主要是为了研究 $Z_{CFP}$ 的表示，由于更专注于实时演奏的音乐信息，因此本文采用了MAPS中的音乐片段集(MUS)部分内容。MUS中每一首音乐都有规范的命名MAPS_MUS_description_instrName.wav，对齐的MIDI标注与其对应的音乐文件名相同。

2) 实验环境

操作系统为Ubuntu16.04，处理器为Intel Xeon(R)CPU E5-2683 v3，频率为2 GHz。实验采用了GPU加速，GPU版本为NVIDIAGTX1080Ti，显存大小为11 GB，显存频率11 MHz，实验过程中使用显存10997 MB。代码运行环境为Python 3.7，Tensorflow1.13，CUDA9.0。

3.2. 实验评价标准

音级转录是一个多分类的问题评价。对于多标签多分类问题，可在时间维度上采用N个二分类器对其进行评价。在二分类中，问题的实际结果被定义为正(Positive)、负(Nagative)两类，模型的预测结果也被定义为正(True)、负(False)两类。

3.3. 实验过程和结果分析

多音级估计实验(Conventional MPE，以下统称C-MPE)，讨论音高识别的准确性，实验在MPAS数据集上进行；

将CFP特征表示方法作为中提出的模型的输入，评估C-MPE在MPAS数据集中的表现性能。实验结果见表1和图5。

F-score能够反映精度和召回率的调和平均，是体现模型性能的平均指标。本文提出的模型在MAPS数据集上的F-score达到了87.92%，高出了文献 [10] 6.5%。

为了获取更直观的效果，本文随机选取了MAPS数据集中ENSTDkCl目录下的一首片段音乐MAPS_MUS-bk_xmas5_ENSTDkCl.wav，截取了其中10~30 s的片段，输入到训练好的模型并将结果可视化，如图6所示。其中，蓝线代表的是TP，绿线代表的是FP，红线则代表了FN。

Table 1. Experimental results of C-MPE based on MAPS

表1. 基于MAPS数据集的C-MPE实验结果

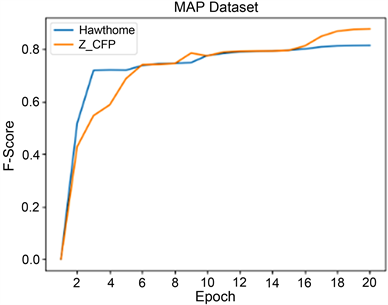
Figure 5. C-MPE experimental training process based on MAPS

图5. 基于MAPS的C-MPE实验训练过程

Figure 6. Model prediction results

图6. 模型预测结果

对于C-MPE实验结果，即使钢琴演奏者们使用了延音踏板，该首钢琴曲中大多数音符都能够被正确识别，并且模型能够比较准确地捕捉它们的起始和结束时间。

4. 总结

本文基于谐波常数Q变换和组合频谱，改进了DeepLabV3语义分割网络，提出一种新的语义分割模型用于转录钢琴复调音乐，取得了良好的效果。实验证明，该方法有效解决了复调音乐产生的谐波重叠与干扰，填补了目前复调音乐转录的空白。

钢琴教育是一种特殊技能教育，家长不能领会其中的教学内容和教学意义，制约了钢琴教学、钢琴练习过程中的规范性，无法实现监督，阻碍了钢琴教育的进一步普及，弹奏练习者需要更多的辅助性指导、陪伴性关怀。

本文深入研究了如何使用人工智能技术，让计算机真正听清楚、听懂弹奏者的钢琴练习，识别和指出“错音”、“错节奏”等常见问题，分析其产生的原因，并为弹奏练习者提供个性化的、陪伴性学习指导。

本文目前涉及到音级估计和乐器匹配，将来还可以考虑更多的音乐特征，比如旋律提取、情感分析等，一方面可以进一步提高转录性能，另一方面为弹奏者的练习提供更丰富的辅助内容和形式。人工智能已经开始打开一个全新的世界，从机器学习、模式识别算法，到基于智能专家系统自动分析推理的反馈式、交互式学习模型，钢琴教育也将从这种新技术所带来的效率提升中受益。

基金项目

湖北省教育厅科学研究计划资助(D20192401)。