1. 引言
随着城市化和工业化的快速发展,中国大气污染问题日益突出、雾霾天气天数增多。造成和加重雾霾天气的罪魁祸首PM2.5 (空气动力学直径小于等于2.5 μm的细颗粒物) [1] 在最近的几十年里被许多国内外学者从各个不同方面展开了细致的研究,其中包括PM2.5的浓度及粒径的时空分布特征研究、污染的因素影响及PM2.5源解析研究等 [2]。PM2.5的化学组成特征拥有较多变化且其形成是多种综合作用的结果,因此,该细颗粒物具有不确定性、随机性和非线性等特点 [3]。对PM2.5浓度进行有效的时间序列分析和时空演化规律探索,不仅有利于管理者发现雾霾天气的内在规律,加深对雾霾演化特点的了解,进一步为国家提供可靠的政策依据,还有利于提高大气污染的防范能力,对了解、预测和防治大气污染有潜在用途。
目前国内对不同时空尺度下的雾霾研究主要考虑到其会随着大气环流等因素影响到邻近地区,较多文献均集中研究雾霾的空间关联特征和不同区域间雾霾浓度的差异性。Mi等 [4] 对黄河中游城市群的时空异质性进行研究,发现该地区 PM2.5浓度具有明显的空间集聚特征,并呈现出春、冬季高,夏、秋季低的特点。邵帅等 [5] 利用空间计量模型研究了影响中国各省雾霾的因素,指出雾霾具有高排放集聚的特征。邓光耀 [6] 结合Dagum基尼系数和Tapio模型,研究了中国2015~2020年雾霾浓度的区域差异以及其与区域发展的关系,发现各大经济区内的PM2.5浓度均明显下降,且呈现出“北高南低,东高西低”的特点。蔡海亚等 [7] 研究了中国各省内雾霾污染强度的区域差异性和收敛性。结果表明,区域发展不平衡是造成差异的主要原因。已有研究对于雾霾时空演化和分析大都是基于计量模型,虽然基于统计学理论和空间计量模型的方法取得了一些具有启发性的结果,但是不能较好的展现序列中存在的模式及其结构信息。
将复杂网络应用于研究跨时空尺度下的雾霾浓度更有利于刻画出不同城市之间雾霾的相互作用关系、结构信息以及演化规律。序列映射到网络的方法可以更加直观地研究从微观到宏观不同时空尺度上的结构模式 [8]。薛安等 [9] 将城市间PM2.5浓度的相关性作为权重构造出了中国城市PM2.5加权网络,并分别按照不同季节和区域的连片度以及模块化Q函数对网络进行划分,研究结果与防治规定提出的“三区六群”大致相同。Jin等 [10] 应用复杂网络中的G算法研究了中国2005年至2014年PM2.5排放的局部空间自相关性,得出在同一区域内不同省份的PM2.5排放会相互影响。马宇博 [11] 根据京津冀各城市 PM2.5数据之间的Pearson相关系数建立了无向网络,采用度、聚类系数、网络效率等综合指标评价了网络节点的重要性。王皓晴 [12] 用转移熵方法构建了有向加权网络模型,对各个节点在整个网络的影响程度进行分析。肖琴 [13] 等人通过对网络的特质性质如节点度、社区结构、模体等性质的有效分析出主要污染城市,空气污染城市具有群聚现象。张晓勇 [14] 等以复杂网络为基础建立了城市PM2.5扩散网络模型。现有基于复杂网络理论研究PM2.5的文献,聚焦于把城市作为网络节点构建复杂网络。这些雾霾序列被映射到了一个静态网络,虽然有效体现了城市间的相互关系,但忽略了雾霾序列内部的动力学特征,不能有效地反映出复杂系统的动态行为及其演化规律。
为解决静态网络无法体现系统内部动力学特征的问题,Lacasa [15] 等人提出可视图作为一种将时间序列映射到复杂网络的方法,该方法可用于拓扑之中来体现底层动力学特征。McCullough [16] 等提出了一种基于可视化小图的时间序列分析方法,将固定大小的窗口沿时间序列滑动,把由此得到的时间序列片段映射为小图,并将每个小图作为对应时间段内的状态描述。Mutua [17] 等在可视小图的基础上将各个可视小图连接为状态转移网络,其对分数布朗运动以及股票市场的研究表明基于可视图模式的时间序列分析方法能够有效提取复杂系统中的动态特征。
因此,本文基于复杂网络理论,使用可视小图的方法,将滑动窗口设定为5小时,同时将上海、杭州、宁波、苏州四个城市的PM2.5浓度序列映射为多个可视小图,再将小图序列映射到状态转移网络。通过计算状态转移网络不同节点的度值、度值比和个别节点位置序列的Hurst指数,得到全连接结构的小图为关键节点的结论。最后使用皮尔逊相关系数、矩阵相关性和网络重合度计算城市相似度,发现宁波、苏州的序列和矩阵相似度最高。
2. 数据与方法
2.1. 数据
本文选取长三角地区距离较近的四座城市上海、杭州、宁波、苏州,自2019年1月1日至2020年12月31日17373个实时PM2.5浓度数据。数据来源于天气后报官方网站(http://www.tianqihoubao.com),若某天缺失超过连续两小时的浓度数据则将该天去除,若缺失一小时的浓度数据则使用插值算法补齐,最后共删去0.98%的数据。
2.2. 可视图理论
可视图(visibility graph, VG)算法常用于提取时间序列的内部信息、描述相应时间序列的结构特征。VG网络继承了原始时间序列的动力学特性 [17]。VG算法的操作步骤如下。首先,将时间序列中的每一个数据点映射为网络的一个结点;然后,结点间有无连边取决于结点是否满足可视性准则:对于任意两点,若它们之间的连线没有被任何位于这两点之间的其他点所截断,则这两个结点“可视”,在可视图网络中可以连接成边。注意原序列中相邻两点间一定“可视”,因为它们之间没有其他数据点阻挡。VG算法的可视性准则如下:
(1)
其中,tb是位于ta,tc之间的任意结点。
以图1为例,依据可视性准则将时间序列中的6个观测点用实线相连,共八条连线,其中观测点“可视”剩余五个结点。
将每个数据观测点看作可视图的结点,满足可视性准则的数据观测点间的连线为网络连边。通常可视图算法被用于对一个完整序列进行运算,本文选取了一个滑动窗口 s遍历整个序列,对每一个窗口内的序列点进行可视图运算,获得的网络结构图称之为该窗口的可视小图。以图1为例,s等于6,该可视小图有6个结点,8条无向边。这样对于一个长度为 N的时间序列,将得到[N/S] ([ ]的含义为取整)个连续的可视小图。可视小图可以用于刻画系统在ti到ti+s-1时刻的状态。在下文中,可视小图将作为转移网络的节点出现。
2.3. 状态转移网络理论
在序列
中,如果状态与状态毗邻,则矩阵元素和相连,由此可得到序列的状态连接链 [18]:
(2)
遍历状态链后,若出现相同状态,则使用其首次状态命名。该过程可以去除重复的状态,并将最终的状态定义为网络节点,从而将原时间序列映射成为状态转移网络 [19]。
状态转移网络中的网络节点度为状态出现的次数,网络节点之间连边的权重则是对应状态之间的转移次数,节点之间连边的方向为状态的转移方向。本文将每种基本图在序列出现的次数称为转移网络的节点度值(Degree),原序列的转移网络的度值与序列随机后对应的节点的度值比值称为度值比。注意,为了便于区分,在可视小图中,用“结点”;在状态转移网络中,用“节点”。
2.4. 扩散熵理论
扩散熵分析方法(Diffusion Entropy Analysis) [20] 是一种基于标度理论,运用香农熵(Shannon Entropy) [21] 来刻画标度不变性 [22] 的分析方法。标度不变性反应了序列当前(或过去)的取值超过最大随机扰动后对该时间序列未来取值的影响程度。在随机扩散过程中,若一个粒子经过 时间发生位移的概率密度函数满足如下形式:
(3)
则称该随机过程满足标度不变性。此时,该随机过程的香农熵满足:
(4)
其中A为常量。
由(4)式可以看出,只要计算出各时间尺度所对应的香农熵,便可通过线性拟合得到标度值。通过扩散熵的计算不仅能提取到自相似的结构特征,还可以定量确定自相似结构系数。扩散熵定量反映了随机过程中一般系统机制的偏离程度。若一个随机过程符合标准布朗运动,则由中心极限定理易得到其标度值为0.5;若标度值大于0.5,则表明该过程在时间尺度上具有内在依赖性,表现形式为粒子后一时刻的位移更容易模仿前一时刻的位移。若标度值小于0.5,则具有内在排斥性,表明此时该粒子与相邻时刻的位移更容易呈相反的趋势。
2.5. 相关系数分析
为了解城市间PM2.5浓度序列相似程度及进一步对比转移网络前后差异,选取皮尔逊相关系数、矩阵相似度和重合相似度三种分析方法计算相关性。皮尔逊相关系数 [23] 是一种广泛用于测量两个变量之间线性相关性的方法。该法基于数据的协方差矩阵来评估两个向量之间关系的强度。通常,两个向量和之间的皮尔逊相关系数为:
(5)
其中
是协方差,
是向量
的方差,
是向量
方差。
矩阵相似度分析,计算公式如下:
(6)
其中
为矩阵相对应转移状态的权重,n为网络的节点数。
重合相似度 [19] 在两个无权网络中为重叠边数乘2与两个网络内总边数之比,计算公式如下:
(7)
其中,e为重叠边数,
和
分别为两个网络内的连边总数。在有权网络中公式则推广为:
(8)
其中,
为示性函数,即满足条件时值为1,不满足条件则为0;
为网络中节点i→节点j的边权,n为网络中的不重复的节点个数。
3. 城市PM2.5浓度序列分析
3.1. 可视小图种类
本文计算了滑动窗口为2到24小时(即2到24个数据点)的小图结构种类。小图种类数目随窗口取值的变大呈指数上升。当窗口小于5,小图结构种类较少。例如,当s = 4时,有10种不同的可视小图结构,节点度值分布平均,没有重要节点,研究意义不大。当窗口大于5,小图结构种类过多。例如,s = 6时,有132种不同的小图,如此多的小图导致每个小图出现的概率很小,则将失去小图的统计意义进一步丢失了研究完整性。综合s大于和小于5的情况,最后选取时间窗口为s = 5小时,构建四座城市的实时PM2.5浓度数据状态转移网络,得到25种网络结构,称之为25种基本图(对应于转移网络中的节点),结果如图2所示。
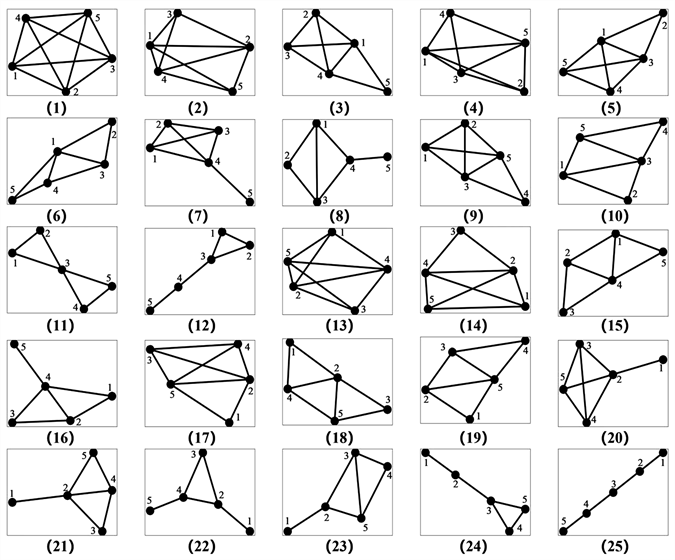
Figure 2. 25 network structures for basic diagrams
图2. 基本图的25种网络结构
3.2. 转移网络的模体及其性质
使用滑动窗口s = 5对四个原序列和对应随机后的序列的分别建立转移网络,并对这两类转移网络的度值、度值比和模体的标度指数等性质进行对比,如图3、图4、图5所示,其中a为上海,b为杭州,c为宁波,d为苏州。
如图3所示,基本图1、12、24在原序列转移网络中的出现次数明显多于序列在随机打乱后,此三种基本图被称为模体(Motif) [24],并分别命名为motif1、motif2、motif3。具体来讲,motif1的网络结构为全连通,即基本图中的五个结点中任意两结点可见,对应的五个数据点在原序列中表现为U型分布;motif2和motif3为对称结构,motif2在仅有相邻连边的基础上加上第一个数据点和第三个数据点连边,即motif2的五个数据点表现为在第二个小时下降,第三个小时到第五小时趋于平稳,motif3在仅有相邻连边的基础上加上第三个数据点和第五个数据点连边,即motif3的数据点表现为第一到第三小时平稳,第四小时下降,到第五小时缓慢上升。该三种基本图背后的雾霾浓度变化是作为PM2.5浓度序列的特性,意味着PM2.5浓度在五小时内常见变化情况为:逐渐快速地上升、逐渐缓慢地下降、逐渐缓慢下降后逐渐快速上升、下降后平稳以及平稳后下降。
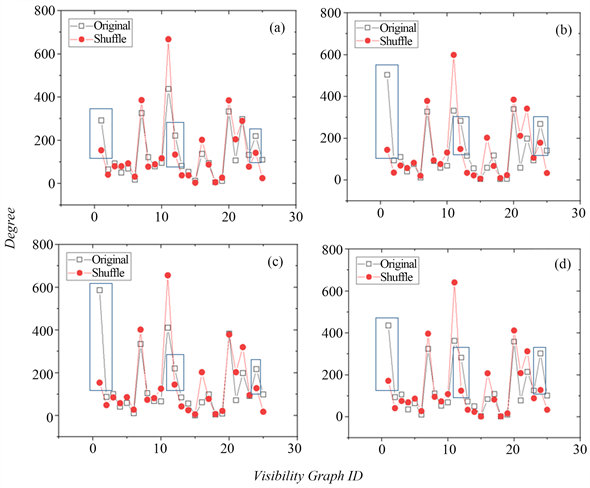
Figure 3. The nodal degree of the base graph
图3. 基本图的节点度
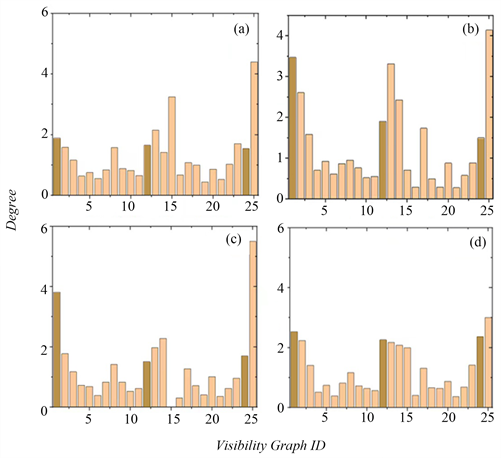
Figure 4. The degree-to-value ratio of the node
图4. 节点的度值比
为进一步对比转移网络与随机网络,图4显示了各个节点与对应随机网络节点的度值比。由图可知,上海、杭州、宁波、苏州的节点度值比在整体分布上呈双U字形且形状大致相似,四个城市中3个模体的比值均较大,其中杭州的motif1度值比为3.5位列四个城市第一,motif2、3在四个城市中的度值比较为平均。当某节点的度值比在1左右时说明该节点在转移网络与随机网络中的度值接近;度值在1上下起伏越大,则说明该节点在转移网络与随机网络中的度值差距越大。从图4(b)中,可以发现杭州是序列随机打乱前后对比差距最大的城市。
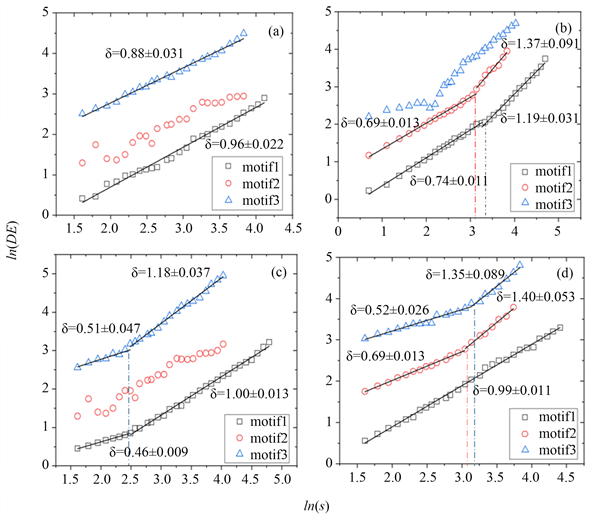
Figure 5. The diffusion entropy of the position sequence of the mold
图5. 模体的位置序列的扩散熵
为进一步研究3个模体是否随机在PM2.5浓度序列中出现,本文提取了motif1、2、3在原序列中出现位置的间隔,形成一个位置间隔序列,并通过扩散熵分析法(DEA)计算Hurst (简称H)指数来说明。若H = 0.5,则表明原序列是随机游走过程;若0.5 < H,则原序列为有偏随机游走,并且序列中存在长程正相关;若0 < H < 0.5,说明序列中存在长程负相关。由图5所示,四座城市motif1的Hurst指数均呈现部分长程相关性。上海motif1的Hurst指数为0.96 ± 0.02,苏州motif1的Hurst指数为0.99 ± 0.01,杭州和宁波的motif1标度指数出现分段现象。其中杭州motif1标度指数的计算窗口在大于大约12.25小时后,斜率发生变化,标度指数由0.74 ± 0.01变为为1.19 ± 0.03;宁波motif1标度指数的计算窗口在大于大约6.25小时后,斜率发生变化,标度指数由0.46 ± 0.01变为1.00 ± 0.03。四个城市的motif2、3则呈现非完全可拟合的状态,其中仅有杭州和苏州两座城市的motif2标度指数能够拟合。杭州motif2的标度指为0.69 ± 0.00,当计算窗口大于12.5小时后,标度指数为0.69 ± 0.001;苏州motif2的标度指数为0.69 ± 0.01,当计算窗口大于后为1.40 ± 0.005,上海motif3的标度指为0.88 ± 0.01。这说明motif1的间隔序列为有偏随机游走过程,并且存在正相关,会大概率发生聚集出现的现象,同时揭示了Motif1存在大量自转移的原因,充分说明了motif1的自转移现象并不是偶然;motif2、3的间隔序列仅在部分城市为有偏随机游走过程。
3.3. 状态转移网络性质分析
本文使用状态转移网络的方法对基本图序列进行计算,获得了四个25 × 25的状态转移矩阵。在求得四个城市所有转移状态的权值后,将其由大到小排序,发现权值的明显转折点为22,于是将其作为临界值 [21],将小于22的权值记为0,得到增强状态的转移矩阵和网络 [25],以及对应随机序列使用相同方法后的增强状态转移矩阵和网络。图6显示增强状态的转移网络示意图。
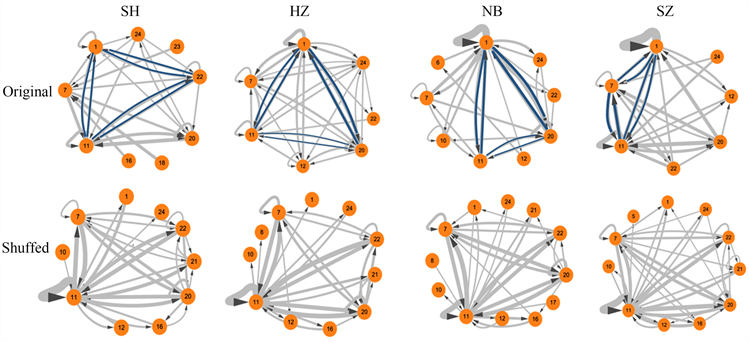
Figure 6. Sequence-enhanced, state-shifted network after the original sequence, completely random
图6. 原序列、完全随机后序列增强状态转移网络
四座城市的最高转移权重如下,上海:节点10→节点20,权值为56;杭州:节点1→节点20,边权值为64;宁波:节点1→节点1,边权值为118;苏州:1→1,边权值为111。四座城市的节点1 (motif1)都存在自连边印证了motif1的出现具有正相关,会出现大量自转移现象。从状态转移网络的结构来看1、11、20三个节点为网络的关键节点,表现为强出度和强入度,连边越粗则表明此两种基本图之间的转移概率越大。上海增强状态转移网络中,1、11、22三个节点相互呈现较强的环状连接,形成一个三边环状;杭州网络和宁波网络中 1、11、20三个节点相互呈现较强的环状连接,呈三边环状;苏州网络中1、7、11三个节点相互呈现较强的环状连接,呈三边环状,且1、7、11三个节点存在自连边,其中节点1也是上文的motif1。结果表明,节点1 (即结点全联通的小图)作为状态转移网络中的重要节点,由可视图模式的定义可以得出,节点1代表的PM2.5数值的变化形式在连续函数中表现为二阶导数大于零,即实际PM2.5浓度变化形式为:逐渐快速地上升、逐渐缓慢地下降或者逐渐缓慢下降后逐渐快速上升,结合motif1存在正相关和存在自连边两个结论,说明PM2.5浓度序列中经常出现以上三种变化情况。
将完全随机后的序列使用相同操作后得到增强状态转移网络,发现关键节点发生了改变,不同城市间的差异被消除,四座城市的网络较为相似,关键节点都变成了节点11,其分别与7、20、22形成双边循环相互转移,且7、11、22节点在四个城市中都存在自连边。通过打乱前后数据的对比,发现节点1重要性被消除,11节点在随机化后成为关键节点;四座城市的三边环状连接并不完全相同,增强后仍保留的节点也不完全相同。
3.4. 相关系数分析
最后,本文研究了这四座城市之间的PM2.5演化相似性。使用皮尔逊相关性方法分析了任两个城市的PM2.5原序列之间的相关性程度,然后分别使用了转移矩阵相关性方法和重合相似度方法分析了任两个城市转移网络之间的相关性程度,结果如表1所示。
三种方法得到的值越大表示相关性越强,如果是0表示完全不相关和1表示完全相关。尽管三种相似度计算方法得到的结果具有差异性,但将每一种计算方法得到的指数前三名标出后发现,宁波与苏州始终是高度相似的;上海与苏州原序列相似度不高,但矩阵相似度和重合相似性都比较高,说明这两座城市的PM2.5演变规律存在相似性。此外通过三种方法均发现上海和杭州相似性较低。
4. 结论
本文使用可见图算法构建长三角地区四座城市PM2.5浓度序列的状态转移网络,用扩散熵算法计算模体位置序列的Hurst指数,实验结果表明,PM2.5浓度序列中存在两种比较显著的规律:1) motif1具有很高的出现频率;2) motif1的出现具有正相关,存在大概率的自转移。结论证实可视小图的方法,相较于其他基于复杂网络理论的方法,有效地挖掘了时间序列内部的动态特征。PM2.5浓度序列中经常出现并且连续出现二阶导数大于零的变化变化情况参考文献,在实际雾霾浓度的变化形式上表现为:逐渐快速地上升、逐渐缓慢地下降、逐渐缓慢下降后逐渐快速上升。相似性分析结果表明宁波和苏州在映射前后都表现较高的相似性,而上海和杭州都表现较低的相似性,上海和苏州原序列相似度较高,而映射后相似度低。
可视图算法作为时间序列转化为复杂网络的一种重要方法,为发掘雾霾序列的内部结构和演化规律提供一个全新的思路。状态转移网络的有向边大小体现了两个基本节点之间的转移概率大小,将模体作为序列内部的特征提取出来,为使用机器学习算法预测雾霾浓度过程中的特征提取提供参考。最后,状态转移矩阵的相似度和网络重叠度均体现了城市间雾霾演化规律的相似性及演化过程的相似度,对城市间治理方案的统筹以及因地制宜制定污染防治政策具有一定的现实意义。由于PM2.5浓度序列具有无标度性质,在未来的研究中,进一步探索PM2.5浓度在其他时间尺度运行的规律,并揭示出PM2.5浓度演化的更深刻规律。
NOTES
*通讯作者。