1. 引言
在现实排队场景中,当排队队列人数过多时顾客往往会发生中途止步(退出)等行为,例如顾客在高峰时期排队一家网红餐厅,当等待时间较长时会发生直接不排队或者中途排队后又离开的行为。面对潜在顾客,服务商往往会采用价格折扣策略吸引更多的顾客加入队列。
在价格折扣策略服务策略下,服务商不仅需要思考价格折扣大小,更需要考虑折扣开始位置对于整个排队队列和其最终利润的影响。当折扣开始位置较前时,服务商服务的人数较多,但是损失了一部分本来可以高利润获取的顾客却只获得了低利润。当折扣开始位置较后时,服务商获得较高的单位利润,但是失去了因折扣而想进入队列的潜在顾客。所以折扣开始位置对于服务商最终获得的利润有重要的影响。因此,研究排队队列的价格折扣开始位置策略对于服务商实现利润最大化有重要意义。
目前排队服务系统中关于服务商利润最大化的文献主要集中在服务定价策略和排队队列类型等方面。因此,本文将从排队服务定价和排队队列类型进行文献综述。
在服务定价的相关文献研究中,一方面是通过设定排队系统的价格来优化服务系统。Naor [1] 首次提出通过价格来影响队长,其假设向顾客收取静态单一费用,并且分析使得服务商获得最大利润的价格高于最优社会收益的价格。Maoui,Ayhan和Foley [2] 考虑了系统存储成本与顾客等待时间成比例,得到了最优价格随系统参数的变化关系。Chen和Frank [3] 在Naor的模型假设下研究了当排队队长小于阈值的动态定价策略,其假设服务商可以随时观测队长并且向顾客收取不同的准入费。Refael Hassin和Alexandra Koshman [4] 针对不可见情形下的M/M/1模型提出了使得服务商利润最大化的高低定价策略,根据当前排队位置和进入阈值来制定价格,并解释了该高低定价的优势。李嘉兴和李军 [5] 基于可观测M/M/1排队系统研究了同质顾客的高低定价策略,并且探讨了该策略如何使得系统最优。刘健等 [6] 研究了顾客存在心理期望等待时间情形下通过折扣对顾客期望值进行调整,并证明该策略比维持原有定价收益更大。谢祥添 [7] 构建承诺交货时间和价格为决策变量的M/M/1模型,得到使企业最优承诺交货时间和最优价格。另一方面服务定价的相关文献主要是通过结合不同场景的特征进行价格制定。李继红等 [8] 基于两种不可见情形研究了休假期服务价格对顾客均衡策略的影响。单琴祺等 [9] 研究具有不耐烦顾客和多重工作休假的M/M/1/N排队库存系统模型,建立系统平均库存费用函数。刘健等 [10] 基于顾客不公平规避心理研究了企业是否对顾客采用分类服务以及如何合理定价。上述文献对排队系统考虑了使得服务商利润最大化的服务定价策略,但是鲜有文献考虑包括折扣开始位置的价格折扣提示策略。
在排队队列类型的相关文献综述中,有较多类型的场景。一方面是关于服务台的休假、故障等情形的研究。李世勇等 [11] 考虑了同步多重休假的M/M/c排队系统,研究了该场景下的顾客止步与服务员定价策略。王勋等 [12] 研究了具有N策略和两种混合休假策略的M/M/1排队系统。蒋毓灵等 [13] 基于M/M/1排队队列考虑了服务台故障场景下的顾客策略行为。另一方面关于顾客差异的研究,例如异质类顾客、顾客不同的等待行为等。刘健 [14] 研究了两类具有不同单位等待时间成本且具有心理期望情境下的优先权定价。单琴祺等 [9] 研究了具有不耐烦顾客和多重工作休假的M/M/1/N排队库存系统模型。Feng Zhang等 [15] 基于工作假期的背景下,研究了完全可见情形和完全不可见情形下的M/M/1顾客的止步策略。
文章主要分析同质顾客到达排队队列时,使得服务商利润最大化的价格折扣开始位置;其次,考虑顾客中途止步的行为,研究该场景下最优的价格折扣开始位置;然后,通过数值实验对公式推导进行验证,分别研究价格折扣开始位置对于服务商利润、中途止步场景下排队队长的影响;最后,对本文的研究内容进行总结归纳,同时指出未来研究方向。
2. 理论基础
研究单一队列的M/M/1排队模型,顾客到达服从
的泊松流,服务时间服从参数为
的指数分布。假设顾客风险中立,进入队列后,不能中途退出。顾客在到达系统时,看到正在排队的顾客有i个(包括正在被服务的顾客),同时企业告知价格折扣开始位置
和价格折扣因子
,即告知价格折扣提示策略
表明服务商在
之后对顾客给予
补贴。顾客根据和服务商告知的价格折扣提示策略
做出进退决策。单一顾客到达系统的价格与排队队列位置如图1:
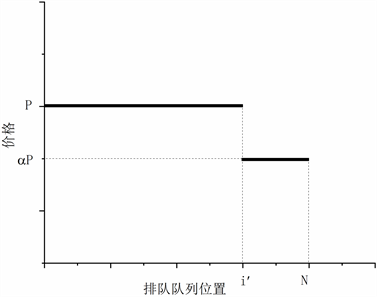
Figure 1. Price discount prompt strategy for a single channel
图1. 单一渠道的价格折扣提示策略
假设顾客进入队列并获得服务需花费P,排队的单位等待时间成本为h,则顾客的效用函数为U,顾客的进入的最大阈值为N:
(1)
(2)
根据顾客的进入阈值得到进入概率为
,潜在到达率为
:
(3)
结合价格折扣提示策略
和队长信息i,顾客到达系统在折扣位置前和折扣位置后的进入概率
和服务商分阶段的利润函数
分别为:
(4)
(5)
联立上述公式(4)和(5),得到服务商利润函数为
(6)
对公式(6)服务商利润函数求导,得出服务商利润最大化的价格折扣开始位置
(7)
2.1. 折扣开始位置与折扣大小关系
研究价格折扣开始位置和价格折扣大小之间的关系。因为
是关于
的函数,所以对
求导可得到价格折扣
与折扣开始位置
的关系:
(8)
分析得到当价格折扣
较小时,最优的折扣开始位置与折扣大小呈负相关;当价格折扣
较大时,最优的折扣开始位置与折扣大小呈正相关。
2.2. 价格折扣前后的服务商利润对比
分析服务商不进行价格折扣策略时的收益函数
和利润函数
:
(9)
对比无价格折扣和有价格折扣策略排队队列的服务商收益和利润函数:
(10)
其中,
和
分别表示由价格折扣策略
时的服务商收益和利润。将同质顾客的最大进入阈值表示成关于价格折扣的一次函数
,则
表示顾客的平均价值,
表示顾客的平均成本。
研究发现,假设顾客进入队列后不会退出队列,此时价格折扣策略的服务队列服务总人数多于无折扣队列,给予价格折扣策略的服务商收益和利润都优于无价格折扣策略。
上述假设顾客在进入队列后不能退出,即顾客只能做出一次进退决策。接下来考虑顾客进入队列后由于排队等待的不耐烦做出的止步,即研究顾客可以做出两次进退决策(进入队伍前和进入队伍后)时的服务商利润。
3. 不耐烦止步场景的折扣开始位置
假设顾客初始的耐心等待时间T,其服从参数为
的指数分布(顾客的耐心等待时间与效用函数无关)。当顾客已经在排队队列时,考虑顾客耐心等待时间T,当顾客的耐心等待时间
时,顾客会离开排队队伍。则顾客在进入队列又退出的概率为
,此时排队队列的真实到达率为
:
(11)
联立公式(5)和(11),得到顾客可两次决策下的服务商利润函数
:
(12)
对
求导得到使得服务商利润最大化的折扣开始时间
:
(13)
在价格折扣提示策略
下,得到考虑顾客不耐烦而造成中途止步的场景下的服务商的收益
和利润
:
(14)
发现
并且
,说明由于顾客的不耐心造成的止步不影响服务商最优的价格策略制定,但是不耐烦的双止步队列服务商利润小于单止步队列。
通过上述研究发现,折扣开始位置对于店铺宣传和服务商利润有重要的意义。在现实的竞争市场中,顾客是复杂的,服务商往往会采用价格折扣策略吸引更多顾客加入队列进行营销。当服务商需要宣传口碑时,较优的折扣开始位置可以尽可能吸引更多的顾客;当服务商希望加入队列的顾客减少中途止步行为时,采用一些活动降低顾客等待过程的不耐烦程度,有助于提高服务商的利润。例如现在很多饭店会在顾客排队等待的过程中进行“免费小吃”、“叠千纸鹤抵现金”等动作。
4. 数值实验
本部分对于考虑价格折扣开始位置的服务商价格折扣策略进行实验,其次分别研究折扣开始位置对于服务利润以及排队队长的影响。不失一般性,假设顾客进入队列并且获得服务的价值
,入场费
,顾客的单位等待成本
,服务商单次服务成本
。本节实验假设
,即顾客到达服务系统时,队列中共有五个人正在排队(包括正在被服务的顾客)。当
时,为确保服务商利润最大化,价格折扣与折扣开始位置的关系如图2所示:

Figure 2. Relationship between quotation strategy and revenue of service providers
图2. 服务商价格策略与收益关系图
当价格折扣提示策略
时,
服务商利润获得最大。通过图2发现服务商收益存在最优的价格折扣开始位置。图3(左)表明第一阶段的顾客数随着价格折扣变大而先减少后增多。图3(右)表明价格折扣策略下的服务商收益优于无折扣场景。
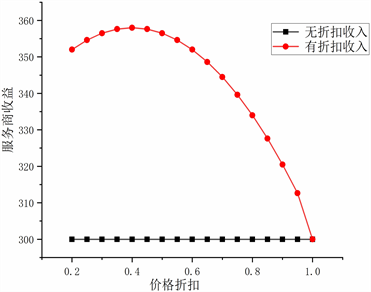
Figure 3. Price discount strategy vs. service provider revenue
图3. 价格折扣策略与服务商收益关系
通过分析无折扣队列和有折扣队列的的排队服务系统,发现两函数之间的纵轴差异为加入折扣策略的增值收益。同时,分析价格折扣与两阶段排队人数的关系如图4所示,当价格折扣
时,
排队队列人数最多且参与折扣的顾客最多;当
时,
原价被服务的顾客最少。

Figure 4. Relationship between price discount strategy and queue numbers
图4. 价格折扣策略与排队队列人数关系
5. 总结与展望
文章主要考虑单一渠道顾客到达时,服务商的价格折扣开始位置策略对其利润的影响,考虑顾客的一次止步和两次止步行为,推导了两种场景下使得服务商利润最大化的最优折扣开始位置表达式。在某一个价格折扣大小下,服务商可以根据最优策略确定价格折扣开始位置,从而实现自身利润最大化。同时,研究发现顾客一次止步场景下的服务商收益和利润都高于两次止步场景,因此服务商需要尽可能减少排队过程中顾客的不耐烦程度。
在现实的排队队列中,大多数排队服务系统是双渠道到达并且顾客是异质性的。未来可以研究双渠道顾客到达场景下的价格折扣开始位置策略,同时可以考虑不同顾客偏好到达等更复杂的排队服务场景。