球形爆炸荷载作用下防护平板试验及模型研究

Test and Model Study of Protective Plate under Spherical Explosion Load

摘要: 球形装药在空气中爆炸，产生的冲击波与平板障碍物碰撞产生的反射超压在防护结构中一般是需要进行控制的，反射超压准确计算与否对于校核结构强度具有极其重要的作用。球形装药在空气中中心起爆之后，经过一球面波传播到平板表面产生一反射波。本文将通过平板反射试验验证了爆炸罐内爆下冲击波压力测试系统的准确性及可靠性，并通过数值模拟进行平板反射试验分析爆炸波通过平板反射后的传播情况，建立了比较符合测试实际的计算模型。计算结果表明，平板试验结果和理论计算值之间误差较小，全部在10%以内，且对称测点的实测结果一致性较好，可以认为构建的冲击波测试系统能够满足圆柱形爆炸容器壳体内壁反射冲击波测试的试验要求。

Abstract: The overpressure caused by the collision between the shock wave generated by the spherical charge exploding in the air and the flat plate obstacle is generally required to be controlled in the protection structure. After the spherical charge detonates in the center of the air, a reflected wave propagates to the surface of the plate through a spherical wave. In this paper, the accuracy and reliability of the pressure test system of shock wave under the implosion of the explosive tank are verified by the plate reflection test. The calculation results show that the error between the plate test results and the theoretical calculation values is small, all within 10%, and the measured results of symmetrical measurement points are consistent with each other. It can be considered that the shockwave test system constructed can meet the test requirements of the reflection shockwave test on the inner wall of the cylindrical explosive vessel shell.

1. 引言

冲击波是爆炸对人员、设备和防护结构产生损伤和破坏效应的主要因素之一，因此对于冲击波的分析和测试在工程领域特别是军工领域有着重要的作用 [1]。爆炸冲击波和目标相互作用中最简单并且研究最多的是爆炸冲击波与平面目标的作用研究 [2] [3] [4] 以及与曲面目标的作用研究 [5] [6]。对于靶板结构的冲击损伤问题，国内外有着大量的研究 [7] [8] [9] [10] [11]。Wharton [12] 分析了商业炸药空中爆炸的实验结果，给出了超压和正向冲量对比距离的依赖关系。将炸药产生的爆炸波处理成点源爆炸产生的球形冲击波，并和的结果作了比较，最后给出适用于较宽范围炸药的TNT等效技术(TNTe)。高永红等人 [13] 基于理想气体的一些理论基础，提出了可供实际应用的空中爆炸近区强冲击波反射地面冲击波参数分布的计算方法。Huffington等 [14] 利用冲量塞技术获得了比距离为0.06~0.2 m/kg 1/3的爆炸冲击波正反射冲量数据。Hu和Glass [15] 从理论上分析了不同炸高对应的不同的冲击波反射现象。爆炸载荷对结构的动力响应问题是一个极其复杂的动力学问题。对于这一问题一般很难给出解析解，一般通过数值方法来研究爆炸载荷与结构相互作用的规律。周保顺等人 [16] 对不同TNT当量和不同炸高下的爆炸冲击波超压分布进行了数值模拟，并进行了试验研究。本文将通过平板反射试验验证了爆炸罐内爆下冲击波压力测试系统的准确性及可靠性，并通过数值模拟进行平板反射试验分析爆炸波通过平板反射后的传播情况。

2. 试验研究

试验设置

为验证爆炸罐内爆下冲击波压力测试系统的准确性及可靠性，本文设计了平板反射试验对测试系统进行校验，如图1所示，钢板的表面积尺寸为1200 mm × 300 mm，厚度为10 mm，整个结构用螺栓固定在钢架上。平板上共设置有5个传感器，其相对位置关系如图2所示，为了保护测试线缆，在钢板横向方向靠近支撑架的位置开孔，线缆从内部穿过，防止试验过程中被破坏。测试时球形装药位于3号传感器正上方，距平板0.4 m，装药质量216 g，共进行了2次重复试验。

峰值压力等试验结果统计如表1所示。

Figure 1. Sensor setup diagram

图1. 传感器设置图

Figure 2. Layout of flat reflection measuring points

图2. 平板反射测点布置图

Table 1. Shock wave parameter result statistics

表1. 冲击波参数结果统计

为验证测试结果的准确性，需对试验结果与理论值展开对比分析。无限空气中球形装药爆炸产生的入射冲击波载荷有多种计算公式，如式1和2所示。根据文献 [17] [18]，当冲击波在固壁面发生反射时，由于入射超压的大小及入射角度的不同，可能发生规则反射和非规则反射，相应的反射超压计算公式分别为：

规则反射：

$\Delta P_{rf}=\Delta P_1\left(2+\frac{\left(\gamma +1\right)\Delta P_1}{\left(\gamma -1\right)\Delta P_1+2\gamma P_0}{\cos }^2\phi \right)$ (2-1)

非规则反射：

$\Delta P_{rf}=\Delta P_1\left(1+\frac{\cos {\phi }_{cr}}{\cos \phi }+\frac{\left(\gamma +1\right)\Delta P_1}{\left(\gamma -1\right)\Delta P_1+2\gamma P_0}{\cos }^2\phi \right)$ (2-2)

其中 $\phi$ 为冲击波入射角， ${\phi }_{cr}$ 为由规则反射过渡到非规则反射的入射临界角。根据公式计算可得平板试验中各测点的反射冲击波峰值压力理论值如表1所示。由表可知，试验结果和理论计算值之间误差全部在10%以内，且对称测点的实测结果一致性较好。综上，可以认为构建的冲击波测试系统能够满足圆柱形爆炸容器壳体内壁反射冲击波测试的试验要求。

3. 数值模型的建立

3.1. 材料模型参数

利用LS-DYNA软件对爆炸荷载下的平板进行模拟，整个模型由TNT炸药和平板两部分组成。炸药材料采用高能炸药材料MAT_HIGH_EXPLOSIVE_BURN和JWL状态方程描述 [19]，状态方程参数如表2所示。

Table 2. Specific parameters of JWL equation of state

表2. JWL状态方程的具体参数

本研究应用的平板尺寸及测点布置如图3所示，P1与P2测点之间距离为150 mm，P1与P3距离为300 mm，P2和P3测点分别对称与P1点两侧。TNT球形装药位于测点1正上方，距平板0.4 m，装药质量216 g，示意图如图4所示。

Figure 3. Tablet size

图3. 平板尺寸

Figure 4. Schematic diagram of the model

图4. 模型示意图

3.2. 数值模拟结果分析

图5给出了216 g炸药下平板从0 ms到0.65 ms的空气压力随时间的变化图。图中各测点均以炸药爆炸时第一个脉冲到达Pl测点的时刻为参照时间，在模型爆炸云图中可以清楚地看到爆炸波的开始和传播过程，0.01 ms时刻爆炸开始后，在0.14 ms冲击波产生的第一冲击波到达平板P1测点附近，对应各测点超压时程曲线P1测点的峰值，在平板的阻挡作用下形成反射冲击波，0.16 ms时到达P2测点处，对应P2测点的峰值，并沿平板向末端移动，于0.25 ms产生马赫波，0.28 ms时到达P3测点处，形成P3测点的超压峰值。如图5所示。在0.45 ms马赫波达到平板两侧尽头发生绕射，并与透过平板表面的冲击波汇聚在平板底部。

Figure 5. Flat pressure cloud

图5. 平板压力云图

图6所示为平板试验仿真中测得的各测点的反射冲击波压力时程曲线，由图可知，仿真反射冲击波压力时程曲线波形良好，曲线较为光滑且噪声较小。数值模拟的压力曲线符合爆炸冲击波反射的基本波形，即有一个很陡的上升沿，冲击波压力达到峰值后开始呈近似指数形式的衰减如图6。

Figure 6. Time history curve of overpressure at each measuring point

图6. 各测点超压时程曲线

3.3. 数值模拟结果及与试验结果的对比

图7为平板上测点在216 g炸药爆炸冲击波峰值压力数值模拟和试验结果及拟合曲线图。为了定量描述试验与数值模拟之间的差异，将爆炸冲击波峰值压力数值模拟结果作为X轴，试验结果作为Y轴，绘制图7(a)，图中斜率为1的直线上表示数值模拟结果与试验结果完全一致，当试验点落于直线下方时，表示数值模拟计算的爆炸冲击波峰值压力比试验值大，当试验点落于直线的上方时，表示数值模拟计算的爆炸冲击波峰值压力比试验值小。从图7(a)中可以直观的看到，试验点基本上都落于斜率为1的实线和斜率为0.80的虚线之间，误差在20%以内，试验值与仿真值误差较小，数值模拟的仿真值比试验值大。

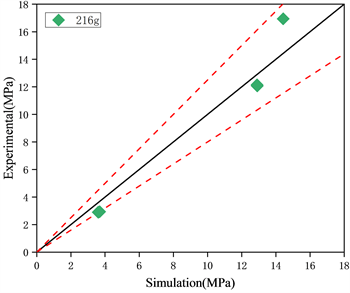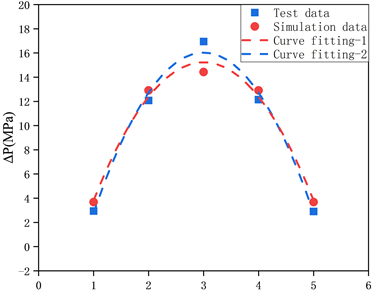(a) (b)

Figure 7. Comparison and analysis of test value and simulation value. (a) Comparison between test value and simulation value; (b) Fitting curve of test value and simulation value

图7. 试验值与模拟值的比较分析：(a) 测试值与模拟值的比较；(b) 试验值与模拟值的拟合曲线

由图7(b)可知，数值模拟与试验结果具有较好一致性，平板测点反射超压峰值由P1测点向两侧逐渐减小。试验值的拟合曲线与数值模拟结果的拟合曲线十分接近，近似重合，说明仿真效果良好。对试验数据和数值模拟的超压峰值用origin进行拟合，结果如图7(b)所示，回归方程为：

$y=B1\ast x+B2\ast x^2+A$

回归模型的采用95%置信区间内的拟合回归系数如下表3所示：

Table 3. Fitting regression coefficient

表3. 拟合回归系数

由于判定系数非常接近1此可以回归方程非常显著且拟合效果较好，故修正后的冲击波反射超压峰值计算公式为：

$y=19.894x-3.316x^2+-13.813$

$y=17.122x-2.854x^2-10.454$

4. 结论

通过将有限元模拟结果与理论分析及试验结果的比较，说明了文中建立的平板结构的有限元模型、流固耦合计算方法以及材料的本构及参数是可靠的。主要得出以下几个结论：

1) 平板试验结果和理论计算值之间误差较小，全部在10%以内，且对称测点的实测结果一致性较好，可以认为构建的冲击波测试系统能够满足圆柱形爆炸容器壳体内壁反射冲击波测试的试验要求，可以科学地分析或预测装备的板结构受高速冲击的响应特性和损伤机理。

2) 仿真反射冲击波压力时程曲线波形良好，曲线较为光滑且噪声较小，试验值的拟合曲线与数值模拟结果的拟合曲线十分接近，近似重合，误差较小，仿真效果好。

3) 通过函数拟合得到各测点的超压峰值拟合曲线，距离越大超压峰值越小。