一种改进型自适应滑模观测器的PMSM控制系统

Control System of Permanent Magnet Synchronous Motor with Improved Adaptive Sliding Mode Observer

摘要: 为了改善传统滑模观测器(SMO)在无感永磁同步电机(PMSM)中转速和转子位置跟踪精度不高的问题，重新设计了一种改进型自适应滑模观测器。采用饱和阈值函数sigmoid代替传统设计中的sign函数；在边界层外引入削弱型积分，用反电动势自适应估计环节来代替低通滤波，提高系统的鲁棒性和反电动势的估算精度；再通过锁相环(PLL)技术来降低估算误差，经过Lyapunov函数来验证算法的稳定性。最后，基于31 W的PMSM实验平台进行算法验证对比出优越性。结果表明，改进型自适应滑模观测器能够实现PMSM的高精度控制同时能达到稳定性要求。

Abstract: To improve the low tracking accuracy of the traditional sliding mode observer (SMO) in non-induc- tive permanent magnet synchronous motor (PMSM), an improved adaptive sliding mode observer (SMO) was redesigned. The saturation threshold function is used instead of the traditional design function. To improve the robustness of the system and the estimation accuracy of the back electromotive force, a weakening integral was introduced outside the boundary layer, and the low- pass filtering was replaced by an adaptive estimation link of the back electromotive force. Then, the phase locked loop (PLL) technology is used to reduce the estimation error, and the stability of the algorithm is verified by the function. Finally, the algorithm based on 31 W PMSM experimental platform is verified and compared. The results show that the improved adaptive sliding mode observer can achieve high precision control of PMSM and meet the stability requirements.

1. 引言

自从人们把变速系统广泛应用于汽车工业，伴随电力电子科学技术、电机控制理论研究及微电力电子技术的发展，交流永磁同步电机(permanent magnet synchronous motor, PMSM)凭借其优越的控制性能，广泛用于高精密数控机床、激光切割、纺织等对系统的精度和可靠性要求严格的领域 [1]。然而PMSM是一个复杂的系统，在实际运行中无法忽略电机参数随运行环境的变化，从而影响控制器的调节性能。矢量控制(vectorcontrol, FOC)的形式主要是 $i_d=0$，为实现电机转子位置和转速信息的实时反馈控制，通过传感器在来采集转子的位置信息和转速信息，但此种方法由于采用了传感器所以不可避免地存在诸如体积、成本、接线复杂、抗干扰能力弱等问题 [2]。为了解决这些问题，国内外学者提出了多种无传感器的PMSM控制方法。滑模观测器法因其鲁棒性好、控制相对精确、响应时间快等优点被广泛使用。

由于滑模观测器自身的工作特性，在干扰大及参数不确定的非线性系统中，能够保持良好的鲁棒性。同时也由于其结构原因，开关的不断切换导致控制的不连续，使得系统出现抖振，采用滑模观测器的系统输出避免不了抖振的产生，为保证系统的强鲁棒性。所以国内外研究方法致力于削弱系统的抖振而不是完全消除，文献 [3] 提供了一种在矢量控制中利用饱和函数代替传统的滑模观测器里面的开关切换函数，从而改善因为高频信号所引起的抖振，提高电机系统的稳定性。文献 [4] 提供了一种新颖的算法思路，提出了一种自抗扰滑模控制器的设计思路，能够精确估计出电机的转子位置，稳态性能良好，但是此算法在实际应用中会由于算法过于复杂而难以应用。文献 [5] [6] 提出了一种滤波反电动势代替法，在边界层结合趋近律对滑模观测器进行饱和函数构造，削弱系统抖振，但此种涉及到反电动势替换的方法会导致相位、幅值的变化 [7]。

本文在传统的滑模观测器的思路上提出了一种新型自适应算法与锁相环(PLL)相结合的技术，将传统的用低通滤波器对转子值进行补偿的环节进行重新设计，用反电动势自适应环节来代替，结合锁相环(PLL)技术 [8] 来提高电机转子位置的准确性识别与转速估计误差缩小。同时提出边界层概念，在滑模面的外层进行积分削弱，柔化控制过程，削弱抖振，提高系统的稳定性，通过Lyapunov函数来验证推导理论的可行性，然后通过Simulink建立PMSM数学模型，通过仿真分析验证改进型自适应滑模观测器的估值准确性和结构稳定性。最后为了进一步验证滑模观测器的可行性，采用DSP28335作为控制板来搭建控制平台，采用3 KW的电机驱动板、规格为“24 v 31 w”的小型永磁同步电机，对算法进行实验验证。

2. PMSM数学模型分析

在两相静止的 $\alpha -\beta$ 坐标系中，定子侧电压、电流及反电动势状态方程为：

$\left[\begin{array}{l}{u}_{\alpha }\hfill \\ u_{\beta }\hfill \end{array}\right]=\left[\begin{array}{cc}R+p{L}_d& 0\\ 0& R+p{L}_q\end{array}\right]\left[\begin{array}{l}{i}_{\alpha }\hfill \\ i_{\beta }\hfill \end{array}\right]+\left[\begin{array}{l}{E}_{\alpha }\hfill \\ E_{\beta }\hfill \end{array}\right]$ (1)

式中： $u_{\alpha }$ 、 $u_{\beta }$ 为定子侧电压分量；R为定子侧电阻；p为微分因子； $i_{\alpha }$ 、 $i_{\beta }$ 为定子侧电流分量； $E_{\alpha }$ 、 $E_{\beta }$ 为反电动势分量；对于式中涉及到的电感 $L_d$ 、 $L_q$ 就要带入到旋转d、q坐标系中来分析。

旋转dq坐标系定义为在静止坐标系下，转子以 $\theta$ 的角速度旋转起来，为了保持相对静止，设定电机定子产生的旋转磁场的角速度与电机转子旋转角速度保持一致，这样的一个坐标系我们称之为dq旋转坐标系，它与坐标系的图解关系如下图1。

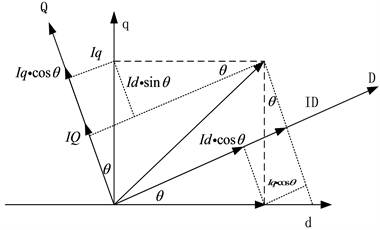
Figure 1. Relation diagram of rotating dq coordinate system and stationary coordinate system

图1. 旋转dq坐标系与静止坐标系关系图

$L_d$ 、 $L_q$ 为旋转 $d-q$ 轴下的电感分量，对于式(1)中的扩展反电动势分量 $E_{\alpha }$ 、 $E_{\beta }$ 满足：

$\left[\begin{array}{l}{E}_a\hfill \\ E_{\beta }\hfill \end{array}\right]=\left[\left(L_d-L_q\right)\left({\omega }_e{i}_d-p{i}_q\right)+{\omega }_e{\psi }_f\right]\left[\begin{array}{r}\hfill -\sin {\theta }_c\\ \hfill \cos {\theta }_e\end{array}\right]$ (2)

由于本文涉及到的PMSM是表贴三相PMSM，存在 $L_d=L_q=L_s$，简化式子(2)得：

$\left[\begin{array}{c}{E}_{\alpha }\\ E_{\beta }\end{array}\right]={\omega }_e{\psi }_f\left[\begin{array}{c}-\sin {\theta }_e\\ \cos {\theta }_e\end{array}\right]$ (3)

由式(3)可知，反电动势在表贴式PMSM应用中仅与电机的转速有关。反电动势与电机转速呈正相关。由此知，做好反电动势的获取，就能够估算转子的位置信息和转速等，再通过对自适应算法的改进，减小估算误差。实现SMO的精确跟踪。

3. 无位置传感器PMSM系统设计

对改进型自适应算法的滑模观测器PMSM的控制系统框图设计如下图2所示。其控制方式采用的是本文所设计的改进型自适应算法，削弱“抖振”的方式采用外层削弱积分型滑模控制方式。

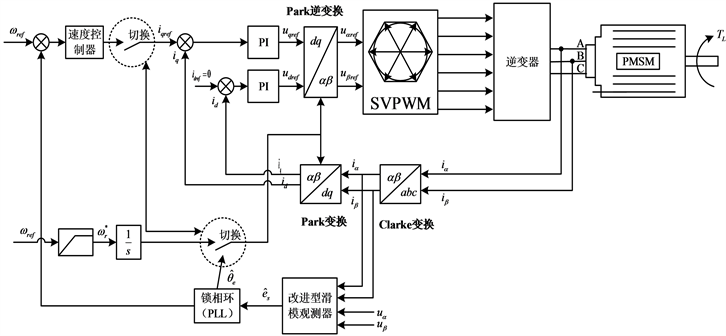
Figure 2. Block diagram of the improved SMO PMSM control system

图2. 改进型SMO PMSM控制系统框图

本文采用的矢量控制方式是 $i_d=0$ 的控制方法，其中 ${\omega }_{ref}$ 为给定转速； ${\hat{\omega }}_e$ 、 ${\hat{\theta }}_e$ 分别为自适应之后的转子转速估计值和转子位置估计值； ${\hat{e}}_s$ 是经过改进型滑模观测器自适应算法修正之后的反电动势 ${\hat{E}}_{\alpha }$ 、 ${\hat{E}}_{\beta }$ ； $i_{abc}$ 、 $u_{abc}$ 分别为在静止坐标系下电机转子的三相电流分量和三相电压分量。为了解决传统SMO设计中存在估计不精确的问题，对传统SMO进行改进，通过改进型自适应观测器出来的反电动势的估计量 进行自适应估计。再通过引入自适应调节参数 $\zeta$ 进行反电动势自适应律的构造，减少 ${\hat{e}}_s$ 估计量中高频谐波分量，柔化波形；采用削弱之后的连续的饱和函数代替不连续的开关函数对电机转子进行值补偿，削弱“抖振”效应。最后通过PLL进行基础信号与反馈信号同步，实现对转子位置和转速的精准估计。

3.1. 改进型自适应滑模观测器设计

由式(1)，分析PMSM模型在两相静止的 $\alpha -\beta$ 坐标系下的电流状态方程及反电动势方程，需将(1)进行变形得：

$\frac{\text{d}}{\text{d}t}\left[\begin{array}{l}{i}_{\alpha }\hfill \\ i_{\beta }\hfill \end{array}\right]=C\times \left[\begin{array}{l}{i}_{\alpha }\hfill \\ i_{\beta }\hfill \end{array}\right]+\frac{1}{L_d}\left[\begin{array}{c}{u}_{\alpha }-E_{\alpha }\\ u_{\beta }-E_{\beta }\end{array}\right]$ (4)

其中：

$C=\frac{1}{L_d}\left[\begin{array}{cc}-R& -\left(L_d-L_q\right)\cdot w_e\\ -\left(L_d-L_q\right)\cdot w_e& -R\end{array}\right]$ (5)

由前文中所提到的由于采用表贴式PMSM，有 $L_d=L_q=L_s$ 成立，则带入式(5)，最后将简化后的C值带入式(4)，有下式成立：

$\frac{\text{d}}{\text{d}t}\left[\begin{array}{l}{i}_{\alpha }\hfill \\ i_{\beta }\hfill \end{array}\right]=-\frac{R}{L}\left[\begin{array}{l}{i}_{\alpha }\hfill \\ i_{\beta }\hfill \end{array}\right]+\frac{1}{L_s}\left[\begin{array}{l}{u}_{\alpha }\hfill \\ u_{\beta }\hfill \end{array}\right]-\frac{1}{L_{\text{s}}}\left[\begin{array}{c}{E}_{\alpha }\\ E_{\beta }\end{array}\right]$ (6)

在传统的滑模观测器的设计中，由于采用的是不连续的sign函数，开关存在一定的延迟，极易产生抖振，且对转子的转子位置和转速的跟踪效果不理想。本文采用一个阈值函数sigmoid来代替sign函数构造估计方程式，sign和sigmoid函数图像对比如下图3，定义sigmoid方程式为：

$\text{sigmoid}\left(x\right)=\frac{2}{1+{\text{e}}^{-\kappa x}}-1$ (7)

Figure 3. Schematic diagram of sign function and sigmoid function

图3. sign符号函数与sigmoid函数示意图

式(7)中，分析sigmoid函数的曲线收敛速度取决于 $\kappa$ 的值，曲线收敛区间为 $\left[-1,1\right]$，当 $\kappa >1$ 时，sigmoid函数是一个单调递增函数，在此条件下 $\kappa$ 的取值越大，函数收敛速度越快，整体响应越快。但是过大的 $\kappa$ 值会导致sigmoid函数接近sign函数，导致边界层厚度变薄，极易产生抖振；同时若 $\kappa$ 取值较小(在 $\kappa >1$ 条件之下)，sigmoid函数曲线越平滑，边界层的厚度越大，鲁棒性越好，但是响应的速度也会相应变慢，影响系统的动态性能。下图4为在不同 $\kappa$ 值下的收敛形态。

Figure 4. Convergence forms of sigmoid under different $\kappa$ values

图4. sigmoid在不同 $\kappa$ 值下的收敛形态

所以选择适当的 $\kappa$ 值才能在保证收敛速度的同时降低滑模抖振。本文选取的 $\kappa$ 值为18。

选取了合适的 $\kappa$ 值，接着构造改进型自适应SMO方程，根据式(6)的简化后的定子电流状态方程，带入电流估计值和自适应之后的反电动势估计值以及sigmoid函数处理之后的观测误差估计值，如下式：

$\frac{\text{d}}{\text{d}t}\left[\begin{array}{c}{\hat{i}}_{\alpha }\\ {\hat{i}}_{\beta }\end{array}\right]=-\frac{R}{L_{\text{s}}}\left[\begin{array}{l}{\hat{i}}_{\alpha }\hfill \\ {\hat{i}}_{\beta }\hfill \end{array}\right]+\frac{1}{L_{\text{s}}}\left[\begin{array}{l}{u}_{\alpha }\hfill \\ u_{\beta }\hfill \end{array}\right]-\frac{1}{L_{\text{s}}}\left[\begin{array}{c}{\hat{E}}_{\alpha }\\ {\hat{E}}_{\beta }\end{array}\right]+C\left[\begin{array}{c}\text{sigmoid}\left({\tilde{i}}_{\alpha }\right)\\ \text{sigmoid}\left({\tilde{i}}_{\beta }\right)\end{array}\right]$ (8)

其中： $\left[\begin{array}{c}\text{sigmoid}\left({\tilde{i}}_{\alpha }\right)\\ \text{sigmoid}\left({\tilde{i}}_{\stackrel{\dot{}}{\beta }}\right)\end{array}\right]=\left[\begin{array}{l}\frac{2}{1+{\text{e}}^{-\kappa \Delta {\hat{i}}_{\alpha }}}-1\hfill \\ \frac{2}{1+{\text{e}}^{-\kappa \Delta {\hat{i}}_{\beta }}}-1\hfill \end{array}\right]$ (9)对于(8)、(9)式中 ${\tilde{i}}_{\alpha }$ 、 ${\tilde{i}}_{\beta }$ 为定子电流观测值； $\Delta {\hat{i}}_{\alpha }={\hat{i}}_{\alpha }-i_{\alpha }$ 为估计误差；其中C满足：

$\{\begin{array}{l}C为负常数\hfill \\ C_{\min }<\left[-\frac{R}{L_s}\left|{\tilde{i}}_{\alpha }\right|-\frac{1}{L_s}\left|\Delta {\hat{E}}_{\alpha }\right|,-\frac{R}{L_s}\left|{\tilde{i}}_{\beta }\right|-\frac{1}{L_s}\left|\Delta {\hat{E}}_{\beta }\right|\right]\hfill \end{array}$ (10)对于式(10)中涉及到的 $\Delta {\hat{E}}_{\alpha }$ 、 $\Delta {\hat{E}}_{\beta }$，结合图2，由以下公式得到：

$\{\begin{array}{l}{\hat{E}}_{\alpha }=-{\hat{\omega }}_e{\psi }_{\alpha }\sin {\hat{\theta }}_e\hfill \\ {\hat{E}}_{\beta }=-{\hat{\omega }}_e{\psi }_{\beta }\sin {\hat{\theta }}_e\hfill \\ \Delta {\hat{E}}_{\alpha }={\hat{E}}_{\alpha }-E_{\alpha }\hfill \\ \Delta {\hat{E}}_{\beta }={\hat{E}}_{\beta }-E_{\beta }\hfill \end{array}$ (11)

其中： ${\hat{E}}_{\alpha }$ 、 ${\hat{E}}_{\beta }$ 为电机的反电动势估计值； $\Delta {\hat{E}}_{\alpha }$ 、 $\Delta {\hat{E}}_{\beta }$ 为反电动势的估计误差， ${\hat{\omega }}_e$ 、 ${\hat{\theta }}_e$ 分别为转子的转速估计值和转子估计位置。

将式(8)减掉式(3)得到电流估计误差方程：

$\frac{\text{d}}{\text{d}t}\left[\begin{array}{c}{\tilde{i}}_{\alpha }\\ {\tilde{i}}_{\beta }\end{array}\right]=-\frac{R}{L_{\text{s}}}\left[\begin{array}{c}\Delta {\hat{i}}_{\alpha }\\ \Delta {\hat{i}}_{\beta }\end{array}\right]-\frac{1}{L_{\text{s}}}\left[\begin{array}{c}\Delta {\hat{E}}_{\alpha }\\ \Delta {\hat{E}}_{\beta }\end{array}\right]+C\left[\begin{array}{c}\text{sigmoid}\left({\tilde{i}}_{\alpha }\right)\\ \text{sigmoid}\left({\tilde{i}}_{\beta }\right)\end{array}\right]$ (12)

3.2. 削弱滑模面函数、反电动势自适应律设计

根据滑模构造原则构造滑模面函数为：

$S=\left[\begin{array}{c}{\tilde{i}}_{\alpha }\\ {\tilde{i}}_{\beta }\end{array}\right]=\left[\begin{array}{l}{\hat{i}}_{\alpha }-i_{\alpha }\hfill \\ {\hat{i}}_{\beta }-i_{\beta }\hfill \end{array}\right]$ (13)

令 $S=\stackrel{\dot{}}{S}=0$，系统处于滑动模态，将式(13)带入式(12)中，得电机反电动势估计效果如下：

$\left[\begin{array}{c}{\tilde{E}}_{\alpha }\\ {\tilde{E}}_{\beta }\end{array}\right]=C{L}_s\left[\begin{array}{l}\text{sigmoid}\left({\tilde{i}}_{\alpha }\right)\hfill \\ \text{sigmoid}\left({\tilde{i}}_{\beta }\right)\hfill \end{array}\right]$ (14)

为了降低滑模面的抖振，在边界层外采用削弱积分设计，引入积分项 ${\displaystyle {\int }_0^t\phi \text{d}\tau }$，边界层内采用了传统积分作用 $\stackrel{\dot{}}{\sigma }=\phi$， $\phi$ 为调节因子；削弱效果可以用 $\frac{\left(\left|S\right|-\mu \right)\left(1+\phi \right)}{2\mu }$ 来衡量，其中 $\mu$ 代表边界层厚度；观察

到削弱效果与 $\left(\left|S\right|-\mu \right)$ 成正比，即当滑模量S的绝对值去掉滑模厚度的差值会对削弱效果造成跳变影响，并不能对削弱效果进行单参数控制，从而在 $\kappa =18$ 时，当系统面处于两倍的边界层上时，控制削弱效果不会发生跳变，这样可以通过调节因子 $\phi$ 来根据实际情况进行削弱调节。

为了使反电动势过度更加平滑，引入自适应参数 $\lambda$，设计相匹配的自适应律，降低后文中锁相环对电机转速和转子位置的误差估计。

采用的表贴式PMSM在一个周期内的加速度可以看作为零，有 $\frac{\text{d}}{\text{d}t}{\omega }_e=0$ 成立，带入式(3)中可得：

$\frac{\text{d}}{\text{d}t}\left[\begin{array}{c}{E}_{\alpha }\\ E_{\beta }\end{array}\right]={\omega }_e\left[\begin{array}{c}-{\omega }_e{\psi }_f\cos {\theta }_e\\ {\omega }_e{\psi }_f\sin {\theta }_e\end{array}\right]={\omega }_e\left[\begin{array}{c}-E_{\beta }\\ E_{\alpha }\end{array}\right]$ (15)

设计如下反电动势自适应律：

$\{\begin{array}{l}\frac{\text{d}}{\text{d}t}{\hat{E}}_{\alpha }=-{\hat{\omega }}_e{\hat{E}}_{\beta }-\lambda {\tilde{E}}_{\alpha }\hfill \\ \frac{\text{d}}{\text{d}t}{\hat{E}}_{\beta }=-{\hat{\omega }}_e{\hat{E}}_{\alpha }-\lambda {\tilde{E}}_{\beta }\hfill \\ \frac{\text{d}}{\text{d}t}{\hat{\omega }}_e={\tilde{E}}_{\alpha }{\hat{E}}_{\beta }-{\hat{E}}_{\alpha }{\tilde{E}}_{\beta }\hfill \end{array}$ (16)

对式(16)进行变形，式(16)整体减去式(15)，对转速的估计减去 $\frac{\text{d}}{\text{d}t}{\omega }_e=0$ 成立的条件。可得：

$\{\begin{array}{l}\frac{\text{d}}{\text{d}t}\Delta {\hat{E}}_{\alpha }=-{\hat{\omega }}_e{\hat{E}}_{\beta }+{\omega }_e{E}_{\beta }-\lambda {\tilde{E}}_{\alpha }\hfill \\ \frac{\text{d}}{\text{d}t}\Delta {\hat{E}}_{\beta }=-{\hat{\omega }}_e{\hat{E}}_{\alpha }+{\omega }_e{E}_{\alpha }-\lambda {\tilde{E}}_{\beta }\hfill \\ \frac{\text{d}}{\text{d}t}\Delta {\hat{\omega }}_e={\tilde{E}}_{\alpha }{\hat{E}}_{\beta }-{\hat{E}}_{\alpha }{\tilde{E}}_{\beta }\hfill \end{array}$ (17)

其中， $\Delta {\hat{\omega }}_e={\hat{\omega }}_e-{\omega }_e$ 为转子转速的误差估计值。构造Lyapunov函数来验证所设计的改进型自适应滑模观测器的稳定性，采用Lyapunov稳定性原理构造如下函数：

$V=\frac{1}{2}\left({\hat{E}}_{\alpha }^2+{\hat{E}}_{\beta }^2+{\hat{\omega }}_e^2\right)>0$ (18)

对该式求微分可得：

$\frac{\text{d}}{\text{d}t}V={\hat{E}}_{\alpha }\frac{\text{d}}{\text{d}t}{\hat{E}}_{\alpha }+{\hat{E}}_{\beta }\frac{\text{d}}{\text{d}t}{\hat{E}}_{\beta }+{\hat{\omega }}_e\frac{\text{d}}{\text{d}t}{\hat{\omega }}_e$ (19)

将式(19)带入式(16)中可得：

$\frac{\text{d}}{\text{d}t}V=-\lambda \left({\tilde{E}}_{\alpha }^2+{\tilde{E}}_{\beta }^2\right)\le 0$ (20)

由上式Lyapunov稳定性证明原理可知所设计的滑模观测器满足稳定性要求。

3.3. 锁相环估计方法设计

本文采用PLL技术来实现电机转速和位置的估计策略，其原理框图如下：

完整的锁相环技术包括压控振荡器、环路滤波器以及鉴相器，对于压控振荡器本文采用的是一个1/S的积分环节，其输出转子的位置估计角；环路滤波器对鉴相器产生的反电动势差 $\Delta E$ 进行高频信号和噪声信号滤波。

为简化计算，令 $\varsigma ={\hat{\omega }}_e{\psi }_f$ ；由式(3)和图5同时将图5可得鉴相器输出的反电动势差为

$\begin{array}{c}\Delta E=-{\hat{E}}_{\alpha }\cos {\hat{\theta }}_e-{\hat{E}}_{\beta }\sin {\hat{\theta }}_e\\ =\varsigma \sin {\hat{\theta }}_{\cos }{\hat{\theta }}_e-\varsigma \cos {\hat{\theta }}_{\sin {\hat{\theta }}_e}\\ =\varsigma \sin \left({\hat{\theta }}^{-}-{\hat{\theta }}_e\right)\\ \approx \varsigma \left({\hat{\theta }}^{-}{\hat{\theta }}_e\right)\end{array}$ (21)

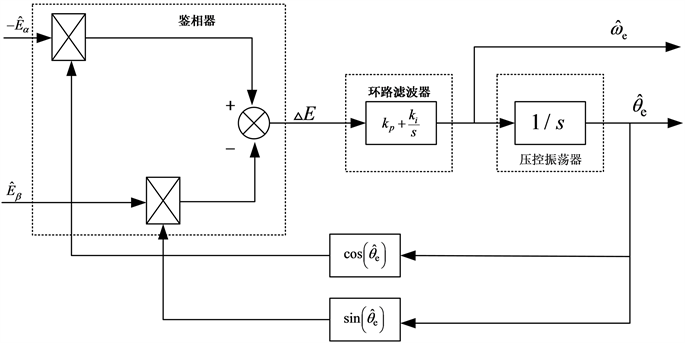
Figure 5. PLL estimation block diagram of speed and rotor position

图5. 转速与转子位置锁相环估计框图

进行结构等效如下图，如下图6：

Figure 6. Structural equivalence diagram of speed and rotor position

图6. 转速和转子位置结构等效图

如图6， $\hat{\theta }$ 为锁相环输入的斜坡信号，可由误差传递函数：

$G_e\left(s\right)=\frac{\Delta {\theta }_e\left(s\right)}{{\hat{\theta }}_e\left(s\right)}=\frac{s^2}{s^2+\varsigma k_{p}s+\varsigma k_i}$ (22)

由式(22)得稳态误差为：

$\Delta e\left(\infty \right)=\underset{s\to 0}{\lim }s\cdot \Delta {\theta }_e\left(s\right)=\underset{s\to 0}{\lim }\frac{s}{s^2+\varsigma k_{p}s+\varsigma k_i}=0$ (23)

由此式可知，此种锁相环设计方式满足转速和转子位置的Lyapunov稳定性试验条件。能够实现位置和转速的较准确估计。

4. 仿真分析与实验验证

运用MATLAB/SIMULINK搭建PMSM调速模型进行仿真验证，电机参数如下。选用规格为“24V 31W”的PMSM作为实验对象，具体参数如下(表1)：

Table 1. PMSM parameters of 24V 31W

表1. “24V 31W”PMSM参数

在进行SIMULINK仿真分析之前要处理好MTLAB系统与原系统相差 $\frac{\pi }{2}$，其原因是一个正切角的估

算值的补偿处理，对于公式(3)变形得：

$\frac{E_{\alpha }}{E_{\beta }}=-\frac{\sin {\theta }_e}{\cos {\theta }_e}=-\tan {\theta }_e$ (24)

即：

${\theta }_e=-\arctan \frac{E_{\alpha }}{E_{\beta }}$ (25)

在仿真中，对于估算角 ${\theta }_{eq}$ 有下式成立：

${\theta }_{eq}终\left(仿真中\right)=\arcsin \left(\frac{-u_1}{u_2}\right)+\frac{-u_2+\left|u_2\right|}{2\left|u_2\right|}\cdot \pi$ (26)

其中： $E_{\alpha }=u_1,E_{\beta }=u_2$。

原因(1)：SIUMLINK中电机自带的坐标系与原系统相差 $\frac{\pi }{2}$ (坐标系定标就差 $\frac{\pi }{2}$ )。

原因(2)： $y=\arctan x$ 函数图像为区域为 $\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$，而实际电机是在 $\left(0,2\pi \right)$，如图7。

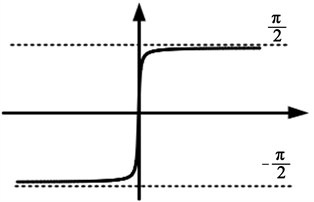
Figure 7. $y=\arctan x$ schematic diagram of the image

图7. $y=\arctan x$ 图像示意图

所以需要在计算正切后，得到角度之后，根据 $u_2$ 的正负，加减一个补偿值，例如 $\left|u_1\right|=1$， $\left|u_2\right|=\sqrt{3}$，当 $u_1$ 为正， $u_2$ 为负，实际位置为 $\frac{5}{3}\pi$，而 $-\arctan \left(\frac{1}{-\sqrt{3}}\right)=\frac{\pi }{6}$，补上坐标系差值 $\frac{\pi }{6}+\frac{\pi }{2}=\frac{2}{3}\pi$，再补上实际电机差异 $\pi$，一共是 $\frac{5}{3}\pi$，这样再仿真模型的电机才能落到实际电机运行中的位置。

首先分析俩模型之间的波形放大对比图，如下图8，在静态转速下，自适应滑模观测器比传统观测器更加平滑且稳定，同时误差更小。

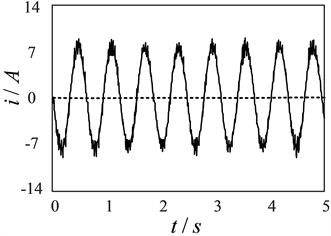(a) 传统滑模观测器 (b) 改进自适应滑模观测器

Figure 8. Stator current waveform at constant speed

图8. 定转速中定子电流波形

如图9，为进一步验证改进型滑模观测器的可行性，本文以TMS320F28335为核心，24V/2A直流开关电源一个，3 KW电机驱动板来搭建PMSM控制平台，如图10，实验参数和仿真参数相同。同表1。

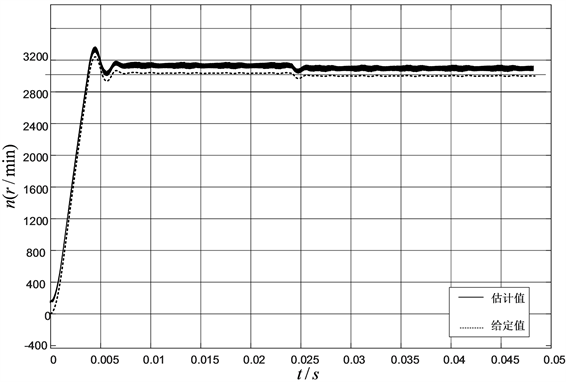
Figure 9. Improved adaptive sliding mode observer speed tracking

图9. 改进型自适应滑模观测器转速跟踪

Figure 10. PMSM improved adaptive sliding mode observer control platform

图10. PMSM改进型自适应滑模观测器控制平台

4.1. 转速跟踪准确性测试

首先进行改进型自适应滑模观测器对比传统的滑模观测器对转子转速和转子位置估计的准确性测试实验，采用转速突变的方法来验证该算法的优越性。在本实验中电机以空载启动，电机以额定转速3000 r/min，在0.025 s时，对电机转速进行突降到2500 r/min，观察两种实验对转子转速和转子位置的跟踪能力。改进型模型中自适应参数 $\lambda$ 定为1000， $\kappa$ 值选定为18，锁相环PI参数 $k_p$ 、 $k_i$ 均选择为3 (仿真中用的试凑法决定的)。两种模型电机转速估计如下图11。

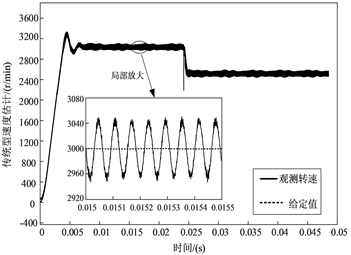(a) 传统滑模观测器 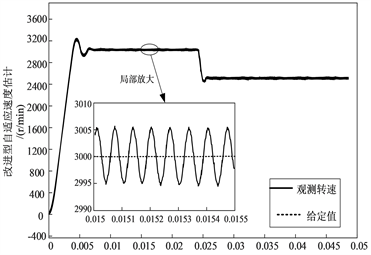(b) 改进自适应滑模观测器

Figure 11. Speed tracking and local zoom under dynamic switching speed

图11. 动态切换转速下转速跟踪及局部放大图

由图11中两个模型所呈现的对比图可以明显看出两种观测器的转速跟踪调节时间误差不超过0.01 s，都能够实现转速的跟踪，但是传统的滑模观测器再0.025 s中给定转速的动态切换中会出现一个毛刺，系统的抖振较为严重；且对比两模型的局部放大波形图，发现传统滑模观测器的误差至少达到了42 r/min，而改进型自适应滑模观测器的转速误差仅为5 r/min，明显更为平滑，谐波更少，抖振更少，相较于传统滑模观测器，改进之后的观测器对转速的估计精度提高了8.4倍，具有更高的观测精度。同时有效降低了动态切换中的抖振。所以改进型自适应滑模观测器在对转速的跟踪精确度更具优势。

4.2. 转子位置跟踪准确性测试

下图12为两个滑模观测在同样给定值速度的情况下的转子位置估计波形和估计误差对比，红色线是电机转子的给定位置信息；黑色线是转子的位置估计值，通过两者的对比可以明显看出，改进型自适应滑模观测器的误差更小，估计更准确。

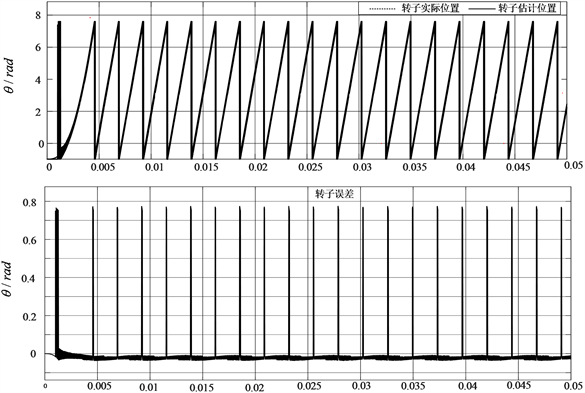(a) 传统滑模观测器转子位置波形及误差(b) 改进型自适应滑模观测器转子位置波形及误差

Figure 12. Comparison of position estimation waveform and estimation error

图12. 位置估计波形及估计误差对比

4.3. 突加负载鲁棒性测试

为测试电机在应对突发情况下的鲁棒性能力，面对扰动时抗干扰能力，改进型滑模观测器是否优于传统型滑模观测器，设计实验如下：如图13，在0.025 s时对俩模型同时施加双倍负载，观察俩模型的转速波形，验证其优越性。

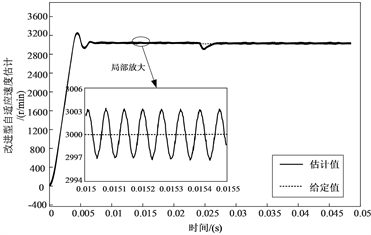(a) 传统滑模观测器突加负载转速波形 (b) 改进型观测器突加负载转速波形

Figure 13. Comparison of position estimation waveform and estimation error

图13. 位置估计波形及估计误差对比

通过俩模型之间的对比，可以明显观察出，改进型自适应滑模观测器具有更好的鲁棒性效果根号，抗扰动能力更强，且波形误差更小，所以改进型自适应观测器更加稳。

5. 结论

本文针对了传统滑模观测器中，对于无位置传感器的PMSM控制系统转子位置估计和转速跟踪不精确的问题，提出了一种改进型自适应算法的滑模观测器，将传统观测器设计中的sign函数用Sigmoid饱和函数代替，选择合适的 $\kappa$ 值，构造自适应律；同时在边界层外引入削弱积分项，进一步降低系统抖振；代替传统的低通滤波器滤器，提出一个反电动势的自适应估计环节优化估计值；PLL技术能够更好的进行转子位置和转速的估计。通过Lyapunov函数验证算法的稳定性和可靠性。最后通过仿真分析和实验验证对比，改进型的自适应滑模观测器的转速、转子位置估计更加平滑，不论是从准确性角度或者从鲁棒性角度，相较于传统滑模观测器优势明显，在转速误差中提高了8.4倍。综上，改进型滑模观测器能满足无位置传感器PMSM系统的控制精确度要求和稳定性要求。能够将传统滑模设计中的sign函数用Sigmoid饱和函数代替，构造自适应律，在边界层外采用削弱积分函数，引入积分调节因子，利用PLL技术进行锁相精确性跟踪，降低抖振，提高跟踪精确度。

NOTES

^*通讯作者。