1. 引言
流数据处理因其在交易分析、故障检测、社交网络、智能广告投放、日志处理和参数分析的广泛应用而受到越来越多的关注,因此,流数据处理能力被视为第三代大数据处理引擎的重要特性之一 [1]。不同于批数据,流数据具有无界性、乱序、分布不均等特点 [2]。无界,指的是数据像水流一样连绵不绝,没有批数据处理最后一条数据的概念。乱序,指的是事件时间更小的数据,可能会因为网络传输延迟、机器故障、节点负载不均衡等问题而后被流数据处理引擎接收并处理。分布不均,指的是数据密集度在时间段范围上存在不稳定现象,即存在数据密集度高低峰现象。如何保证在这些特性下处理结果的准确与低延迟,这对流数据处理引擎提出了相较于批处理引擎更多且复杂的挑战 [3]。
Apache Flink [4] 是当下最热门的流处理引擎之一,它提供的低延迟、高吞吐、高可用等流处理能力,使它被众多企业广泛地应用于解决流处理需求。Flink以WaterMark的策略来处理乱序数据 [5],WaterMark被视为Flink系统中的全局事件时间,WaterMark = 数据事件时间 − 延迟宽容度,是它的计算方式。Flink依赖WaterMark来触发各种计算操作。因此,延迟宽容度的设置紧密关联着Flink系统各类型计算的触发,这极大地影响了Flink的吞吐量、处理延迟、准确率等性能指标。
文献 [6] 研究表明,延迟宽容度的设置需要根据数据流特性设定,如果延迟宽容度设置过大,虽然保证了结果的准确性,但会导致处理延迟过高。如果延迟宽容度设置过小,虽然处理延迟低,但是可能会导致结果不准确。目前,常见的做法 [7] [8] 是根据数据平均延迟时间,作为延迟宽容度参数取值,但因为流数据具有爆发性以及数据分布差异等特点,数据流在时间上往往分布不均匀,除了常见的均匀分布,数据流还可能呈现正态分布和指数分布。如果简单基于数据平均延迟时间作为延迟宽容度,可能导致在特定时间段或者整体上,数据处理延迟高或统计结果不准确等问题 [9]。
文献 [10] 比较了几种批处理引擎的性能差异,但没有对流处理引擎进行测试。文献 [10]、 [11]、 [12] 针对流处理引擎设计了数据处理管道,并对多种性能指标进行了测试与分析,但是没有对数据差异对引擎的影响展开分析,实验用的是同一种数据。本文选择了3种不同分布流数据,分别为正态分布、均匀分布、指数分布。围绕这三种数据,设计了一套基于Flink的数据处理管道,用于测试这三种数据在Flink流处理引擎平台的性能指标,并探讨如何针对不同特征的流数据设置延迟宽容度,进而提高Flink引擎的吞吐量、处理延迟、准确率等性能指标。
2. 负载设计
2.1. 数据处理管道设计
为给出不同流数据对Flink性能影响的比较分析,本文基于Flink Api设计了一套数据处理管道,如图1所示。数据处理管道总共由4个算子构成。实验将围绕着不同的延迟宽容度设置下,Flink引擎对这三类数据的准确率、处理延迟、吞吐量等性能指标的影响展开。在管道中,Source为数据源算子,用来读取Kafka中字符串格式消息,并将字符串数据转换成JavaBean对象;Filter为过滤算子,用来检查数据是否符合实验要求,如果不符合,则中断实验;Window为滚动窗口,搭配Trigger与聚合算子,统计窗口数据个数与处理延迟;Sink为数据输出算子,将实验结果输出到MySQL存储。

Figure 1. Flink data processing pipeline
图1. Flink数据处理管道
2.2. 待测流数据特征
本文的流数据由建模生成,数据密度特征来自于“百度统计”所覆盖的百万站点及APP网络流量密度,该特征记录了一天各小时的流量密集度。因为数据生成不是本文讨论范畴,所以不展开介绍。下面介绍本文待测流数据的分布特征与延迟特征。
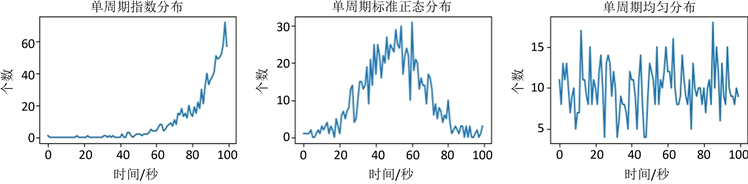
图2展示了本文三种待测数据的单周期数据分布与全周期数据分布,本文窗口概念,指的是一个长度确定的时间段。

Table 1. Statistical indicators of random delay time
表1. 随机延迟时间统计指标
单周期数据分布,指的是一个窗口内数据分布情况。本文取窗口长度100秒。利用不同的概率密度函数,在窗口内进行随机数据生成,从而确定各时间点生成多少个数据。为了效果显著,在图2(a)~(c)中,各单周期分布累计生成了1000个数据。
全周期数据分布,由846个长度100秒的单周期窗口组合而来(一天 = 84,600秒)。每个窗口具体生成数据个数,由“百度统计”流量密集度特征所确定。
观察图2(d)~(f)可以发现,三种全周期数据的数据分布整体走势基本相同,该走势符合本文采集的流量密度特征。
由于流数据应该还具有延迟属性,所以本文基于指数分布,为数据添加随机延迟扰动。生成的随机延迟扰动的统计学指标,如表1所示,表1展示了三种数据的平均延迟时间、众数延迟时间、百分位延迟时间等统计指标。
 (a) (b) (c)
(a) (b) (c)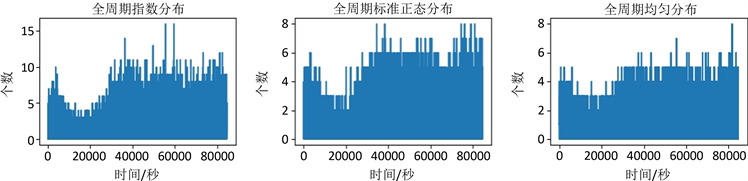 (d) (e) (f)
(d) (e) (f)
Figure 2. Data distribution characteristics
图2. 数据分布特征
3. 实验结果与分析
3.1. 实验环境
本文使用的集群由3台计算机节点组成,系统为Centos 6.9。节点的硬件配置为1核2线程CPU,4 GB内存,80 GB硬盘。节点安装的软件为Zookeeper 3.4.10、Kafka 2.1.1、MySQL 5.7、Flink 1.10,其中,Zookeeper、Kafka、Flink均以分布式方式运行在三个节点上,MySQL实例只运行在一个节点上。
3.2. 窗口统计准确率
1、计算方式
(1)
窗口统计准确率计算公式,如公式(1)所示。ηi为第i个窗口统计准确率;Ci为第i个窗口聚合统计值,它表示第i个窗口触发计算后窗口所含的数据个数;Si为窗口密集度值,窗口密集度值由“百度统计”流量密集度特征所确定。由于部分属于窗口 的数据会因数据延迟导致“迟到”被丢弃,所以窗口统计准确率是一个介于0~1之间的数值。
2、实验结果
取延迟宽容度为0进行实验测试,数据窗口聚合统计结果,如图3所示,图中实线表示由“百度统计”流量密集度特征所确定的理论值;虚线表示基于数据处理管道计算所得的实际值。如果虚线与实线贴合的愈加紧密,则表示数据丢失的越少,窗口统计准确率越高,反之,如果虚线与实线相隔越大,则表示数据丢失越多。分析此图,可得出以几点结论:
1) 数据密集度对准确率的影响
区间250~846内理论数据密集度最高,区间150~250理论数据密集度较低。依此划分,进一步观察虚线,区间250~846内虚线波动越剧烈与实线分离程度较高,区间150~250内虚线波动较小,基本贴合实线。此现象可能是因为当流引擎在高数据负载的情况下,产生背压(流引擎数据处理速度,跟不上数据输入速度),导致数据丢失。因此,数据密集度会影响窗口统计的准确率,数据密集度越高的时间段内,数据聚合统计准确率越低。
2) 数据分布对准确率的影响
三种不同数据的统计准确率有着明显的差别,指数分布数据的虚线波动范围最大,均匀分布数据虚线波动适中,正态分布数据虚线近乎贴合实线。导致此现象的原因是,指数分布数据大量集中在窗口末段,所以受延迟扰动的影响最大;正态分布数据集中在窗口中段,延迟扰动对数据的影响不大;均匀分布数据有部分数据分布在在窗口末段,所以有一定的影响。因此,数据的概率分布会影响窗口统计的准确率,指数分布数据统计准确率最低,正态分布数据统计准确率最高,均匀分布数据统计准确率低于正态分布,但也有较好的统计准确率表现。
 (a) (b) (c)
(a) (b) (c)
Figure 3. Experimental results of window statistical accuracy
图3. 窗口统计准确率实验结果
3.3. 窗口处理延迟
1、计算方式
(2)
窗口处理延迟时间计算公式,如公式(2)所示。Li为第i个窗口处理延迟;tci为第i个窗口关闭的机器时钟时间;toi为第i个窗口开启的机器时钟时间。窗口i的开启与关闭与WaterMark和Trigger算子的设计密切相关,每当流处理引擎接收到一条新数据时,都会为此数据生成一个WaterMark,而Trigger算子会根据数据的事件时间属性,来决定是否要开启或关闭一个窗口。
2、实验结果
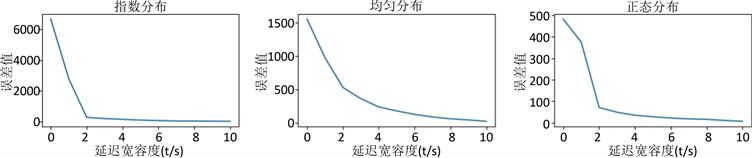
取延迟宽容度参数从0到10进行实验测试,总聚合误差值与总处理延迟时间的实验结果,如图4所示,总聚合误差值M = ∑(Si − Ci),总处理延迟L = ∑Li。分析此图,可得出以几点结论:
1) 延迟容忍度对误差值与处理延迟的影响
观察图4(a)~(c),可以发现误差值随延迟宽容度的增加而下降,即误差值与延迟宽容度成反比关系,观察图4(d)~(f),可以发现处理延迟随延迟宽容度的增加而上升,即处理延迟与延迟宽容度成正比关系。
此现象是因为对于一条数据来说事件时间是确定的,当延迟宽容度增加,则WaterMark值减少,因为WaterMark = 数据事件时间 − 延迟宽容度,所以当延迟宽容度增加,虽然窗口关闭时间被延后导致处理延迟增加,但是窗口能接收到更多的“迟到”数据,误差值随之下降。因此,延迟宽容度参数值会影响聚合统计的准确性与数据处理延迟,通常延迟宽容度设置的越大数据聚合统计误差会越小,直至趋于0为止。而对于处理延迟来说,它会随着延迟宽容度的增大而增大。
2) 数据分布对处理延迟的影响
观察图4(d)~(f),三种不同数据的误差值与处理延迟的曲线变化斜率有着显著差别。
对于误差值来说,当延迟宽容度为0时,指数分布数据误差值最大,正态分布数据误差值最小,均匀分布数据介于两者之间,并且指数分布与正态分布数据的误差值,拥有一个数量级的差距。但是随着延迟宽容度的增加,指数分布数据的误差值下降最为迅速,能快速收敛到与正态分布数据同等误差值水平,而均匀分布数据下降速度较慢,曲线更加平缓。
对于延迟时间来说,延迟宽容度的增加,会导致指数分布数据的处理延迟在激增后趋于平稳,而均匀分布与正态分布数据处理延迟增长较为线性。
因此,数据的概率分布会影响窗口的统计误差值与处理延迟时间,当延迟宽容度为0时,指数分布数据统计误差最高,但是随着延迟宽容度的增加,误差值下降极快,但处理延迟时间也会大幅度上升。对于正态分布数据,即使延迟宽容度为0,也拥有很好的误差值表现,但是延迟宽容度的增加,误差值下降与处理延迟增长的收益不如指数分布数据。
 (a) (b) (c)
(a) (b) (c)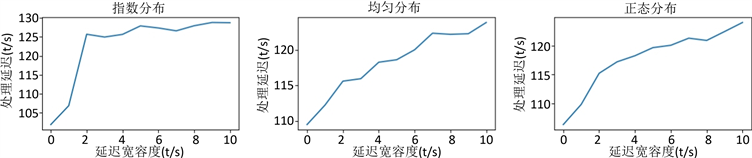 (d) (e) (f)
(d) (e) (f)
Figure 4. Experiment results of delay tolerance, error value and processing delay
图4. 延迟宽容度与误差值和处理延迟实验结果
3.4. 吞吐量
1、计算方式
(3)
吞吐量的计算公式,如公式(3)所示。T为吞吐量;∑Ci为公式(1)中Ci求和;∑Li为公式(2)中Li求和。
2、实验结果
1) 延迟宽容度对吞吐量的影响
由图5可以发现,吞吐量基本上随着延迟宽容度增加而减少,即吞吐量与延迟宽容度成反比关系。此现象的主要是因为,虽然延迟宽容度的增加能导致窗口处理更多的“迟到”数据,但是该指标的增加幅度不如处理延迟大,所以导致了吞吐量呈下降趋势。
因此,延迟宽容度参数值会影响引擎数据吞吐量,通常延迟宽容度设置越大,引擎数据吞吐量会越小。
2) 数据分布对吞吐量的影响
三种不同分布数据吞吐量指标有着明显的差距,当延迟宽容度为0时,正态分布数据的吞吐量指标最高,但是随着延迟宽容度增大,正态分布与均匀分布数据,数据吞吐量趋于一致。对于指数分布数据来说,它随着延迟宽容度增大有一个吞吐量上升的范围,这验证了图4中前段范围指数分布数据的误差值骤降的现象,然而随着延迟宽容度增加,指数分布数据的吞吐量大幅度下降,这验证了图4指数分布数据,处理延迟大幅度上升的现象。
因此,从整体来看,随着延迟宽容度的增加,三种分布数据吞吐量都呈现下降趋势,但是指数分布数据的吞吐量,会大幅度低于正态分布与均匀分布数据。从局部来看,指数分布数据有一个小范围的吞吐量增益期,它会随着延迟宽容度的增大而增大。
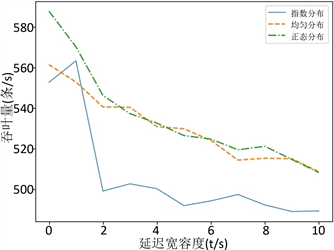
Figure 5. Experiment results of delay tolerance and throughput
图5. 延迟宽容度与吞吐量实验结果
3.5. 延迟容忍度选择
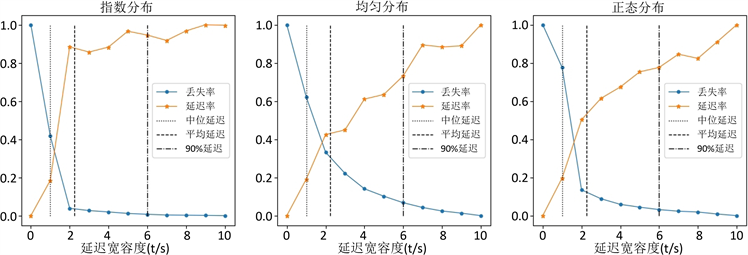
对总聚合误差值 和总处理延迟 ,采用公式(4)进行归一化处理,将其转变为丢失率与延迟率。再选取表1中位数延迟(50%延迟)、平均延迟、90%延迟作为延迟宽容度参考轴,来探讨三类流数据的延迟宽容度选择。
(4)
1、指数分布
观察图6(a),可发现指数分布数据,在0~中位数延迟范围内,数据丢失率下降极快,而延迟率只是缓慢提升;中位数延迟~平均数延迟范围内,丢失率继续大幅下降,但是延迟率迅速提升;中位数延迟~90%延迟,丢失率极其缓慢下降,延迟率小幅度提升;90%延迟之后,丢失率趋于收敛,延迟率继续保持小幅度上涨。
结合图4综合分析,指数分布在延迟宽容度为0时,存在大量数据丢失,所以设置大于0的延迟宽容度十分必要,并且小幅度设置此值后,就能得到很好的丢失率与处理延迟比。
因此,如果对准确率要求较低,可在0~中位数延迟内选择延迟宽容度,如果准确率要求较高,可在中位数延迟~平均数延迟范围内选择。
2、均匀分布
观察图6(b),可发现均匀分布数据的延迟率与丢失率,随延迟宽容度的变化较为线性,并考虑到图4中均匀分布数据,在延迟宽容度为0时误差值适中(远低于指数分布)。
因此,如果准确率要求较高,可选择90%延迟后作为延迟宽容度,如果要求较低,可选择0~平均延迟作为延迟宽容度。
3、正态分布
观察图6(c),可以发现正态分布数据在0~平均延迟范围内,丢失率下降极快,而延迟率上升明显更缓和;平均延迟之后,延迟率上升趋势明显快于丢失率下降趋势。
结合图4综合分析,正态分布在延迟宽容度为0时,误差值已经很低。
因此,如果对准确率要求不是过于严格,可以设置延迟宽容度为0,如果,对准确率有进一步要求,可以考虑在0~平均延迟范围内做出选择。
 (a) (b) (c)
(a) (b) (c)
Figure 6. Experimental results of delay time, loss rate and delay rate
图6. 延迟时间与丢失率和延迟率实验结果
4. 结语
本文设计了一套基于Flink的数据流处理管道,将不同特征的流数据导入管道进行实验分析和研究,基于实验得出的结果详细地探讨了不同延迟宽容度对Flink的准确性、处理延迟、吞吐量等性能指标的影响,并分析了导致实验结果产生的可能的因素。在此基础上,提出了对于不同特征流数据的延迟宽容度的设置方法。实验结果表明,针对大规模流数据,使用本文提出的方法,结合流数据自身的特征设置延迟容忍度,能够有效地提高流数据处理引擎处理具有乱序特性的流数据的准确率,并降低处理延迟,从而达到改善流数据处理引擎性能的目的。