基于本征正交分解法的缸内流场循环变动特性分析

Analysis of Cyclic Variation Characteristics of Flow Field in Cylinder Based on Proper Or-thogonal Decomposition Method

摘要: 应用本征正交分解(POD)方法对数值模拟的发动机多循环速度场数据进行分析，以深入考察发动机缸内速度场循环变动特性。结果表明，POD方法可以将速度场分为不同阶模态，能反映不同程度的流场结构。分析了不同模态对应的时间系数标准差随曲轴转角的变化情况，揭示了缸内速度场循环变动大小随发动机曲轴转角的变化的规律，即进气阶段速度场循环变动要大于压缩阶段速度场循环变动。

Abstract: The Proper orthogonal decomposition (POD) method was used to analyze the numerical simulation of engine multi-cycle speed field data to deeply investigate the cyclic variation characteristics of the engine velocity field. The results show that the POD method divides the velocity field into different order modes, reflecting different degrees of flow field structure. The change of the standard devia-tion of the time coefficient corresponding to different modes with the crankshaft angle was analyzed, and the law of the change of the cyclic change of the velocity field in the cylinder with the rotation angle of the engine crankshaft was revealed, that is, the cyclic variation of the velocity field in the intake stage was greater than that of the velocity field in the compression stage.

1. 引言

由于发动机缸内流场瞬变的特点，研究发动机缸内流场变化时，既要考虑循环内的湍流脉动，也要考虑到循环间的循环变动 [1]。传统的发动机缸内循环变动分析方法基本上都是对发动机多循环数据进行相平均，得到流场的平均信息和脉动信息，以流场平均信息表征该工况下发动机稳定工作时的缸内流场状态，以流场脉动信息表征该工况下的发动机循环变动特性。但是，采用这种统计平均的方法得到的是循环变动的整体信息，对循环变动的分析仍不够深入，无法探究流场脉动信息中更为细致的不同尺度的流场特征 [2] [3]，比如大尺度的拟序结构信息和小尺度的湍流脉动信息，具有明显的局限性。本征正交分解(proper orthogonal decomposition, POD)作为一种有效的降维方法，该方法能从原始数据库中提取在均方意义下的正交基模态，来描述数据集合的特征。对湍流场而言，POD可将瞬态速度场表示为一组模态(POD模态)的线性组合，模态之间线性无关，即每组模态分别反映出原瞬态流场的不同结构特征 [4] [5]。基于POD方法研究瞬态速度场的优势，Fogleman等 [6] 利用POD方法分析发动机缸内的滚流破碎，将POD模态作为低维模型基来分析流场的动态特性。伟武 [7] 等利用POD研究了湍流速度场，发现了临界条件下，湍动能与涡旋之间的关系。顾鹏 [8] 等利用本征正交分解的方法，分析发动机的特征模态与循环变动，阐述了含能流场与局部小涡团之间的特征差异。秦文瑾等将本征正交分解应用于缸内瞬态流场，提出POD四分解法，分析了发动机缸内流场经过四分解后各自流场在时间和空间上的变化特性，研究了发动机缸内流场的拟序结构，验证了POD可以用来作为湍流场数值模拟结果准确性的有效工具 [9] [10]。

本文通过POD方法对缸内速度场进行循环变动分析，对同一时刻多周期的速度场数据集合进行处理，提取出POD模态，利用这些模态对应的速度场结构还原原始速度场结构，以得到发动机缸内流场循环变动的细节信息。

2. POD数学原理

发动机缸内湍流场是高维的非线性系统，POD方法能够有效的进行降维近似，利用低维系统来近似描述原高维非线性系统。对非线性湍流流场 $u\left(x,t\right)$ 的线性近似，首先需要确定一组基函数，使得非线性湍流流场 $u\left(x,t\right)$ 在基函数上的投影与原流场具有足够高的相似性 [11] [12]，数学表达式为：

$\max \frac{\left({\left|u\left(x,t\right),\phi \left(x\right)\right|}^2\right)}{\left[\phi \left(x\right),\phi \left(x\right)\right]}=\frac{\left({\left|u\left(x,t\right),\psi \left(x\right)\right|}^2\right)}{\left[\psi \left(x\right),\psi \left(x\right)\right]}$ (1)

当满足下式时，则基函数即为符合要求：

${\displaystyle {\int }_{\Omega }{R}_{ij}}\left(x,y\right){\psi }_j\left(y\right)d_y=\lambda {\psi }_i\left(x\right)$ (2)

式中， $R_{ij}\left(x,y\right)=\left(u\left(x,t\right),u\left(y,t\right)\right)$ 表示流场内两点的二阶相关Hermit矩阵， $u\left(x,t\right)$ 在基函数上的投影是不相关的，通过投影到基函数，原高维的非线性场被线性分解，表达式如下：

$u\left(x,t\right)={\displaystyle {\sum }_{k=1}^{N_{mode}}\left(a^k\left(t\right){\psi }^k\left(x\right)\right)}$ (3)

通过上式可以发现，原始流场被分解为两部分，与空间相关的基函数 ${\psi }^k\left(x\right)$ 和与时间相关的系数 $a^k\left(t\right)$，同时时间系数 $a^k\left(t\right)$ 也是不相关的。接着将二阶相关Hermit矩阵对角化：

$R_{ij}\left(x,y\right)={\displaystyle {\sum }_{k=1}^{N_{mode}}\left({\lambda }^{\left(k\right)}{\psi }_i^{\left(k\right)}{\psi }_j^{\left(k\right)}\right)}$ (4)

式中， $N_{mode}$ 表示模态数， $\lambda$ 表示矩阵的特征值。此外，对二阶相关Hermit矩阵 $R_{ij}\left(x,y\right)$ 进行缩放积分后即可得到流场总能量E：

$E=\frac{1}{2}{\displaystyle {\int }_{\Omega }u\left(x,t\right)u\left(x,t\right)\text{d}x}=\frac{1}{2}{\displaystyle {\sum }_{k=1}^{N_{mode}}{\lambda }^{\left(k\right)}}$ (5)

不同模态的特征值大小可以反映各模态对流场动能的贡献程度，最大特征值对应的POD模态包含了原流场的大部分能量，其它模态包含的原流场能量依次递减 [13]。

3. 计算结果与分析

发动机缸内燃烧过程中循环变动是发动机在某个工况下稳定运行时，连续的循环间缸内燃烧状态发生变化，燃烧过程不一致的现象，燃烧过程循环变动具体体现在缸内压力变化、火焰传播及发展情况变化以及发动机输出扭矩表现不一致。本文以在AGCO 84AWI六缸共轨柴油机的基础上改造而来的一款单缸光学发动机为模型，选用CONVERGE软件来模拟发动机的多循环工作过程。根据表1所示的光学发动机基本参数建立几何模型，将其以STL的格式导入到CONVERGE中。将几何模型划分成进、排气道、进、排气门、气缸壁、气缸盖、活塞等不同的边界，紧接着进行发动机整体参数的设置，之后依次进行物性及组分设置、求解器设置、输出文件设置、物理模型设置以及网格加密设置，其中算例的边界与初始条件如表2所示，经过计算建立出速度场数据库。

Table 1. Main parameters of optical engines

表1. 光学发动机主要参数

Table 2. The initial and boundary conditions of the study

表2. 算例的初始条件和边界条件

3.1. 缸内速度场瞬态循环变动特性分析

影响缸内流场运动状态的最主要因素是进气射流作用和活塞运动时对气流的引导作用，进气射流在进气过程中由于受到进气道、进气阀、燃烧室以及气缸壁等结构的导向作用会产生大尺度的涡流(swirl)结构以及滚流(tumble)结构 [14]。发动机在实际工作过程中进气和压缩阶段缸内速度场变化剧烈，并且不同循环间速度场也具有差异性。图1为进气中段−270˚CA ATDC时不同循环的瞬态速度场对比，为排除初始条件对缸内流场的影响，对比从第二个循环开始。以压缩上止点为0˚曲轴转角(CA)，图中左侧为排气道，右侧为进气道。结合Y-Z平面速度云图和速度等值面三维图(图中所示速度等值面数值分别为10、50、90)不难发现，进气道一侧包括气缸中心区域和气缸壁附近的速度较大，这是因为进气射流随进气道进入缸内，形成滚流，此外还在气缸壁的导向作用下形成涡流，加速了周围空气流动 [15]。对比不同循环下的速度云图可以明显发现，尽管速度分布具有一定的共性，即进气道一侧气缸中心区域和气缸壁附近速度较大，但是各循环间缸内速度场具有明显的循环变动。在气缸中心区域由于进气射流高速流入，与周围空气发生强烈的剪切作用，因此会产生较大的湍动能；而在气缸壁附近，进气射流进入后顺着气缸壁形成涡流，与此同时，进气射流与缸壁发生摩擦也会产生湍动能。因此，这些区域湍流运动较强，湍流脉动又具有随机性，强烈的湍流脉动必然会加剧这些区域的速度场在不同的循环间呈现分布的不一致性。

Figure 1. −270˚CA ATDC velocity field multicycle comparison

图1. −270˚CA ATDC速度场多循环比较

图2为压缩中段−90˚ CA ATDC时不同循环的瞬态速度云图及矢量图，从图中可以看出压缩阶段缸内流场整体流速相较于进气阶段明显减小，尤其是进气阶段流速较高的进气道一侧的气缸壁附近，从速度云图来看整个缸内速度分布不再出现进排气道两侧差异明显的情况。这是因为此时进气射流的作用消失，同时活塞上行压缩缸内气体，使得气体整体向上运动，缸内流场一致性增强，各向异性趋势被遏制。观察不同循环间的Y-Z平面(只截取缸内部分)的速度矢量图也能发现这一特点，速度场整体流向较为一致，气缸中心区域速度方向均随活塞向上，仅在燃烧室附近的气缸壁两侧形成大小不一的速度涡团，这是因为活塞上行挤压气缸壁和燃烧室附近的气体形成缸内挤流运动。X-Y平面呈现的是缸内涡流场，观察速度云图发现整体空间分布较为均匀，这是因为缸内涡流运动是顺着气缸壁进行，使得整个气缸内产生沿着壁面的周向气流运动，因此气缸壁附近的速度反而比缸内中心区域大。结合不同平面的速度云图和速度矢量图可以发现压缩阶段不同循环间的流场循环变动相较于进气阶段有所减小，原因是射流作用消失和活塞对缸内气体的整体压缩削弱了流场各项异性，从而使得缸内速度场循环变动降低。

3.2. 基于POD的速度场循环变动特性分析

速度场POD分解能够发掘出发动机循环变动的更多细节信息，在对缸内速度场进行循环变动分析时，POD能够对同一时刻多周期的速度场数据集合进行处理，提取出一系列基函数，也叫POD模态，通过这些模态对应的速度场结构可以还原原始速度场结构。本文使用MATLAB软件运行POD分解程序对模拟计算得到的发动机多循环速度场数据库进行运算处理，得到一组POD模态，不同模态间的能量强度差异体现在该模态对应的特征值大小，将特征值按照从大到小依次排列后，首位特征值对应的POD模态即包含了原速度场的大部分能量，或者说体现了原速度场整体的平均特性，其余模态包含的速度场能量依次减少，各模态含能递减的趋势可以反映该速度场整体的循环变动程度。模态1对应的特征值较大，且远大于其余模态对应的特征值时，则可以说明该组数据整体一致性较强，流场的脉动量较小，代表该组缸内速度场数据整体的循环变动较小，此时速度场的绝大部分能量可以被前几个POD模态所包含。除了通过分析特征值随模态数目增加时的衰减速度来判断循环变动大小以外，还可以通过分析POD分解时得到的另一个参数——时间系数的变化情况来反映速度场循环变动的大小。通过分析模态对应的时间系数的统计参数，比如标准差，来反映该组速度场数据的循环变动大小。

3.2.1. POD模态对应的特征值分布

图3为进气中段−270˚ CA ATDC时刻和压缩中段−90˚ CA ATDC时刻Y-Z平面和X-Y平面速度场分解后的各POD模态对应的特征值分布情况。从图中可以看出：首先所有曲线的走势都较为一致，并且模态1的特征值要远大于其余模态的特征值，随着模态数目的增加，特征值迅速减小，且基本都在第5个模态时特征值减小到接近于0。压缩阶段模态1对应的特征值较大说明流场能量分布较为集中，此时流场的绝大部分能量被前几个模态所包含，并且特征值曲线下降的速率更大，说明此时流场流动的一致性较强。将进气阶段和压缩阶段的特征值分布曲线对比来看，进气阶段的模态1对应的特征值要小于压缩阶段的模态1对应的特征值，并且从特征值的衰减速度来看，压缩阶段的特征值衰减更快，这说明压缩阶段相较于进气阶段流场一致性更强，循环变动更小。进气阶段存在的进气射流使得缸内产生强烈的湍流脉动，增大了流场的不稳定性，造成循环间的不一致性增大，而压缩阶段由于不存在进气射流的影响，并且活塞上行使缸内气体一致向上运动，减弱了流场运动的不一致性，循环间差异性减小。由此可见，进气射流和活塞运动是影响发动机运行时流场循环变动的重要因素。

此外，对比Y-Z平面(滚流平面)和X-Y平面(涡流平面)的速度场POD分解后得到的特征值分布情况可以发现，两个平面的特征值十分接近，特征值衰减的规律也较为一致，说明其作为发动机缸内流场的典型截面，在反映缸内流场循环变动特性时具有代表性和准确性。

Figure 2. Multi-cycle comparison of −90˚CA ATDC transient velocity cloud and vector plot

图2. −90˚CA ATDC瞬态速度云图及矢量图的多循环比较

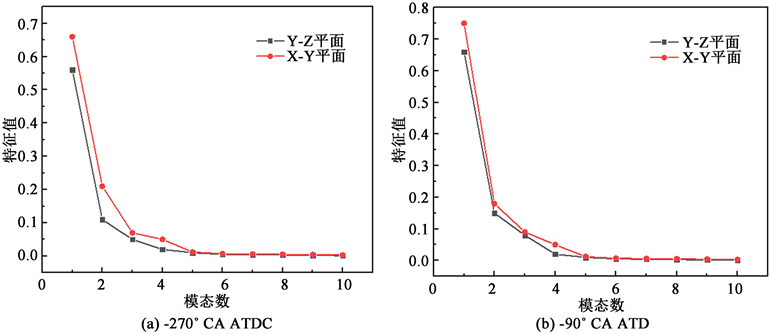
Figure 3. Distribution of characteristic values of each mode after the decomposition of velocity field POD at different times

图3. 不同时刻下速度场POD分解后各模态特征值分布

3.2.2. POD模态分析

速度场经过POD分解后所得到的各阶模态将原始速度场内包含的不同尺度的速度场结构作了划分，从低阶模态到高阶模态速度场结构尺度依次减小，实现了细分不同循环的瞬态速度场。按照特征值递减得到的这组有序模态也反映了瞬态速度场含能结构的分布情况，以所得的各阶模态来对比分析原始速度场能够更清晰地分析小尺度的涡团结构的演变情况。此外，通过分析POD模态对应的时间系数的标准差变化情况来判断发动机进气阶段和压缩阶段的速度场循环变动大小的变化规律。

图4为进气中段−270˚ CA ATDC时刻和压缩中段−90˚ CA ATDC时刻X-Z平面速度场前三个模态与原始速度场集合的相平均无量纲化后的云图对比，原始速度场数据是模拟计算的10个工作循环的数据。观察模态1和原始速度场相平均无量纲化的云图可以发现二者相似度非常高，无论是云图整体形态分布还是数值大小，说明模态1能够准确还原速度场的大尺度结构，包含了原速度场的大部分动能。模态2相比模态1整体分布较为分散，局部出现了小的涡团结构，说明其所包含的能量向原速度场小尺度涡团能量过渡。到模态3中，小尺度涡团则更加明显，这些小尺度涡团能够很好地反映原始速度场中的湍流扩散和涡团拉伸、破碎后的小尺度结构，也包含了这部分小尺度流场结构的动能。以上分析说明，从低阶模态到高阶模态，所反映的流场结构越来越小，捕捉到原流场局部小尺度随机涡团的能力也越来越强。因此，随着模态数目增加，原流场中能量较小的小尺度涡团结构逐渐从大尺度结构中区分开来，流场结构组成更加清晰明了，通过POD分解后能够更加准确、细致地分析流场结构的循环变动规律。

图5为不同模态的时间系数标准差随曲轴转角的变化情况，图(a)为有量纲的时间系数变化曲线，图(b)为无量纲化后的时间系数标准差变化曲线。从图(a)中可以看出，在进气过程中，各阶模态的时间系数标准差均增大，并且在进气中后段−240˚ CA ATDC左右达到最大值，随后逐渐减小。模态1的时间系数标准差在压缩中前段−120˚ CA ATDC左右下降到最小值，之后又有所上升。除此之外，模态2和模态3的时间系数标准差均为单调减小，但是二者的时间系数标准差在数值上始终要大于模态1的时间系数标准差。这说明速度场循环变动在进气阶段逐渐增大，并在进气中后段达到峰值，随后压缩阶段循环变动减小。图(b)为无量纲化后的各模态的时间系数标准差随曲轴转角的变化情况，其整体趋势与无量纲化前有所区别，因为不同时刻缸内速度场总动能变化较大，对各模态对应的时间系数大小也产生影响。各模态时间系数的标准差均在进气阶段逐渐增大并达到峰值，但是后续压缩阶段发现模态2、模态3的时间

Figure 4. Comparison of X-Z plane velocity field decomposition POD modes at different moments

图4. 不同时刻X-Z平面速度场分解POD模态对比

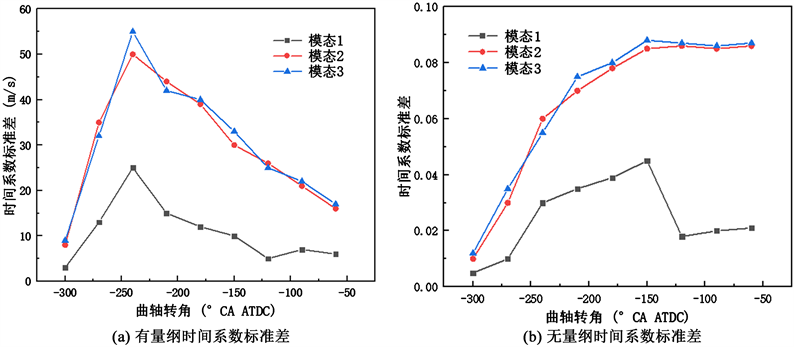
Figure 5. Change of standard deviation of time coefficient with crankshaft angle for different modes

图5. 不同模态的时间系数标准差随曲轴转角的变化情况

系数标准差减小趋势不明显，而模态1的时间系数则相对有较明显的减小。不同模态间时间系数标准差变化的差异性体现了原速度场中不同尺度的含能结构的循环变动差异性，模态1代表的是缸内速度场的大尺度含能结构，类似传统速度场相平均后的平均流场，其循环变动并不是所有含能结构中最大的。相反，模态2和模态3的时间系数标准差在数值上始终较大，说明其代表的缸内速度场含能结构的循环变动较大，或者可以说模态2和模态3所代表的速度场结构的循环变动特性在整个速度场循环变动中发挥着重要作用。

4. 结论

本文主要利用POD方法对发动机缸内速度场进行分析了，研究了进气和压缩阶段缸内流场的变化情况以及模拟的发动机多循环数据的循环变动特性。主要结论如下：

1) 各阶模态的时间系数标准差均增大，在进气中后段达到最大值，随后逐渐减小。模态1的时间系数标准差在压缩中前段左右下降到最小值，之后又有所上升。模态2和模态3的时间系数标准差均为单调减小，但是二者的时间系数标准差在数值上始终要大于模态1的时间系数标准差。表明速度场循环变动在进气阶段逐渐增大，并在进气中后段达到峰值，随后压缩阶段循环变动减小。

2) 通过分析不同模态对应的时间系数标准差随曲轴转角的变化情况，揭示了缸内速度场循环变动大小随发动机曲轴转角的变化规律，即进气阶段速度场循环变动要大于压缩阶段速度场循环变动。不同模态间的时间系数标准差的变化差异体现了原速度场中不同尺度的含能结构的循环变动差异性，模态2和模态3所代表的原速度场结构的循环变动特性在整个速度场循环变动中发挥着重要作用。

NOTES

^*第一作者。

^#通讯作者。