基于优化的NURBS曲面G¹连续拼接实现

Research on G¹ Continuity Optimization Theory Based on NURBS Representation Surface

摘要: 航天飞机、汽车数字模型等零件对拼接处要求C¹/G¹连续，因此本文提出面向NURBS曲面进行G¹连续性优化算法理论。首先根据NURBS曲面求取连续性方程并作为约束，通过设置控制点与权值作为优化目标，利用拉格朗日乘子法进行约束求解得到G¹连续后的控制点和权值，将得到的控制点和权值带回到原曲面实现在拼接处C¹/G¹连续。为了保证曲面在优化后变化尽可能的小，将变化前后的控制点与权值乘积作为优化问题，控制点前后变化的差值为优化条件，通过设计算法将数值经过数次迭代得到NURBS曲面C¹/G¹拼接时的最优解。结果表明，该方法能够实现控制点及权值的数值优化，并对于NURBS曲面高阶连续优化、多片拼接以及NURBS三维模型的连续性优化提供借鉴意义。

Abstract: Space shuttle, automobile digital model and other parts require C¹/G¹ continuity at the splice, so this paper proposes G¹ continuity optimization algorithm theory for NURBS surfaces. First, the con-tinuity equation is obtained according to the NURBS surface and used as the constraint. By setting control points and weights as the optimization objective, the constraint solution is performed using the Lagrange multiplier method to obtain the control points and weights after G¹ continuity. The control points and weights are brought back to the original surface to achieve C¹/G¹ continuity at the splice. In order to ensure that the surface changes as little as possible after optimization, the product of the control points before and after the change and the weight value is taken as the opti-mization problem, and the difference between the changes of the control points before and after the change is taken as the optimization condition. The optimal solution for NURBS surface C¹/G¹ splicing is obtained through several iterations of the design algorithm. The results show that the method can realize the numerical optimization of control points and weights, and provide reference for the higher-order continuous optimization of NURBS surfaces, multi piece splicing, and continuity opti-mization of NURBS three-dimensional models.

1. 引言

样条曲面拼接技术常用于三维模型的构建，是曲面造型中常用方法。为了利用NURBS曲面对机械零件进行表达，可采用创建式 [1] 或重建式 [2] 模型构建。重建式方法应用更为广泛，对于曲线曲面的拟合范围较大，容易丢失细小特征存在误差。创建式方法则更加符合建模习惯，需要手动计算曲线、曲面和体的控制点、节点矢量等参数，可以表达一些细小特征。

NURBS曲面拼接在公共边界处多为C⁰连续，对于公共边界出现尖点的情况会导致分析结果数值偏大，不符合机械零件的加工要求。在模型表达过程中，对于一些精度要求较高的模型，采用C⁰连续往往难以达到分析要求，其得到的结果比较差。因此，对于模型的构建实现G¹连续优化非常有必要。传统NURBS曲面实现G¹拼接时，将某一曲面上的参数设定为0，修改另一曲面参数，这种方法会导致曲面出现变形过大导致的曲面形变情况。

针对利用B样条连续拼接，赵岩 [3] 提出对于单节点和重节点双五次曲面连续性条件，陆亚文等人 [4] 提出一种用于NURBS曲面G²光滑拼接算法，对于精确控制双片NURBS曲面的G¹连续具有重要意义。王崇 [5] 提出通过反求控制点的位置，利用NURBS曲面的连续性条件进行约束，实现了NURBS曲面近似光滑拼接的办法。在NURBS曲面研究上，车翔玖，梁学章等人 [6] [7] 提出了实现NURBS曲面拼接的G¹、G²连续条件。陆亚文等人 [8] 采用调整参数思想，通过设定内部控制点将插值点作为参考，达到实现曲G²光滑拼接的效果，此方法相较于传统NURBS曲面拼接方法有更好的局部修改性质。

基于B样条和NURBS的不同以及目前的研究，本文将主要探讨NURBS曲面在拼接时，根据NURBS曲面方程性质，求取其拼接时的连续性条件做约束，以控制点和权值的变化情况作为优化问题。通过设置优化边界条件，多次迭代得到最优解，实现对边界处连续性进行优化，建模质量的提高，通过求解模型雅可比数值验证算法的准确性和鲁棒性。

2. NURBS曲面连续性基础理论

2.1. NURBS基础理论

B样条在表达自由曲线曲面时，具有更好的优势，但是当曲线曲面是初等曲线曲面时，利用B样条进行造型表达就显得捉襟见肘。因此，为了弥补B样条表达的缺陷，就有学者提出非均匀有理B样条(NURBS)的造型方式。其相较于B样条，增加了权因子，用于控制曲线到控制多边形的距离，采用该造型方式，能够更好的表达初等曲线曲面。

由于非均匀有理B样条也属于B样条范畴，因此其继承了B样条的所有性质。其主要包括以下几个特性：1) 仿射不变性：经过变化后的NURBS曲线曲面仍保持原来的性质不发生改变；2) 连续且可微：NURBS的基函数在节点矢量集合中无限次可微；3) 局部修改性：对于表达NURBS曲线曲面上的控制点，可以通过修改局部控制点P时，该过程仅对控制点P对应的矢量集合有效；4) 非零性：在任意半开区间的矢量集合中，至多存在p + 1个非零的基函数数值。

NURBS曲线曲面的表达式主要由基函数和权因子组成，基函数可以通过递推公式求解得到。如下所示为基函数的表达：

$N_{i,0}\left(u\right)=\{\begin{array}{l}1,若u_i\le u<u_{i+1}\\ 0,其他\end{array}$ (1)

$N_{i,p}\left(u\right)=\frac{u-u_i}{u_{i+p}-u_i}{N}_{i,p-1}\left(u\right)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}\left(u\right)$ (2)

其中： $N_{i,p}\left(u\right)$ 表示第i个p次B样条基函数， $i\in \left[0,n\right]$， $u_i$ 称为节点，节点矢量 $U=\left\{u_0,u_1,\cdots ,u_m\right\}$ 是一个单调不减的实数序列。

当曲线曲面次数为p时，可以表示为：

$C\left(u\right)=\frac{{\displaystyle \underset{i=0}{\overset{n}{\sum }}{\omega }_i{N}_{i,p}\left(u\right)P_i}}{{\displaystyle \underset{i=0}{\overset{n}{\sum }}{\omega }_i{N}_{i,p}\left(u\right)}}$ (3)

其中， $P_i$ 是曲线上的控制点， ${\omega }_i$ 是控制点对应的权值， $0\le {\omega }_i\le 1$，首末控制点权重大于0。

值得注意的是，当权值大小为1的时候，NURBS退化成B样条曲线，NURBS也因此继承了B样条所有性质，且可以用于表达圆锥曲线。权值的大小影响曲线靠近控制多边形的距离，当权值越大，曲线就越接近控制多边形，反之亦然。

对于曲面在U、V方向次数分别为p^u、p^v的模型，当给定曲面上控制点 $P_{i,j}$，以及对应的权值 ${\omega }_{i,j}$。可以用表达式表达为：

$S\left(u,v\right)=\frac{{\displaystyle \underset{i=0}{\overset{n}{\sum }}{\displaystyle \underset{j=0}{\overset{m}{\sum }}{\omega }_{i,j}{N}_{i,p}\left(u\right)N_{j,q}\left(v\right)P_{i,j}}}}{{\displaystyle \underset{i=0}{\overset{n}{\sum }}{\displaystyle \underset{j=0}{\overset{m}{\sum }}{\omega }_{i,j}{N}_{i,p}\left(u\right)N_{j,q}\left(v\right)}}}$ (4)

NURBS曲面具有和B样条曲面同样的性质。

2.2. 连续性基础理论

为了研究曲面的连续性，需要先理解曲线连续性的相关内容。曲线曲面间光滑度的度量主要包含：参数连续性和几何连续性。参数连续性是指组合参数曲线拼接处有n阶的左右导数相同，可以实现n阶可微，一般用Cⁿ表示，几何上C⁰，C¹，C²分别表示曲线曲面的形状、切线方向以及曲率连续；几何连续性是指于切线、切平面、曲率等几何量所定义的曲线和曲面拼接处的连续性。G⁰连续与C⁰连续一致；G¹连续又称为切平面连续，在其公共连接线处具有处处连续变化的切平面或者相同的法线方向；G²连续又称为曲率连续，要求在公共连接线有处处相同的法曲率，如下图1所示为几何连续的几种情况。

Figure 1. Geometric continuity

图1. 几何连续

由于参数连续性比较严格，在几何设计中不够直观，并且严重依赖于参数的选择，因此对于同一条曲线，当其参数发生变化时，其参数连续性也会发生改变。因此，在本文中衡量模型连续性则采用几何连续性，优化后的NURBS面片的雅可比值与优化前的雅可比值进行对比验证优化算法的有效性。

3. 双片拼接G¹连续性条件

3.1. B样条曲面G¹连续性条件

传统B样条曲面在拼接时，如图2所示。S¹、S²分别表示两个曲面参数方程，其连接处需要严格满足C⁰/G⁰连续，为了实现其连接处的控制点满足G¹连续，就需要求解B样条的G¹连续性方程。

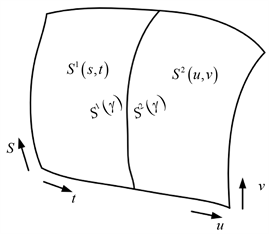
Figure 2. Splicing two NURBS surfaces

图2. 两NURBS曲面拼接

模型拼接如上图2所示，其中S¹、S²具有相同的v方向，在拼接处的两边t和u方向相反，根据B样条曲线曲面的G¹连续性条件方程为：

$\alpha \left(v\right)\frac{\partial S^1}{\partial t}\left(0,s\right)+\beta \left(v\right)\frac{\partial S^1}{\partial t}\left(0,s\right)+\gamma \left(v\right)\frac{\partial S^2}{\partial u}\left(0,v\right)=0$ (5)

其中， $\alpha \left(v\right),\beta \left(v\right),\gamma \left(v\right)$ 是分段多项式函数， $\frac{\partial S^1}{\partial t}\left(0,s\right)$ 表示S¹对(0, v)处，对u方向求偏导，对其化简可得：

$S_u^1\left(0,v\right)=\alpha S_u^2\left(0,v\right)$ (6)

其中， $\alpha$ 为连续性系数。

3.2. NURBS样条曲面G¹连续性条件

由此，根据B样条连续性方程可以推导NURBS曲面的连续性方程。假设两NURBS曲面分别为B¹、B²在拼接处需要先实现G⁰连续拼接，即两者具有公共连接线。想要实现求解NURBS曲面连续性条件就需要先对曲面方程进行求导，根据NURBS曲面公式可以令 $X={\displaystyle {\sum }_{i=0}^n{\displaystyle {\sum }_{j=0}^n{\omega }_{i,j}{N}_{i,p}\left(u\right)N_{j,q}\left(v\right)P_{i,j}}}$， $Y={\displaystyle {\sum }_{i=0}^n{\displaystyle {\sum }_{j=0}^n{\omega }_{i,j}{N}_{i,p}\left(u\right)N_{j,q}\left(v\right)}}$，由此曲面表达式可以简写成：

$N=\frac{X}{Y}$ (7)

对其进行求导可以得到：

$N_u=\frac{X_u-N*Y_u}{Y}$ (8)

因此通过计算NURBS曲面再拼接处(0, v)处的偏导矢并带入到上述求导公式可以得到：

$N_u\left(0,v\right)={\displaystyle \underset{j=0}{\overset{m}{\sum }}{N}_{j,q}\left(v\right)}\frac{p}{u_{p+1}}\frac{w_{1,v}}{w_{0,v}}\left(P_{1,v}-P_{0,v}\right)$ (9)

根据公式分析，NURBS曲面连续性取决于曲面上控制点、权值以及节点矢量有关，将上述公式带入到了G¹连续公式可以得到其G¹连续性方程，当两个曲面次数p、节点矢量u都相同时：

$\frac{w_{1,i}}{w_{0,i}}\left(P_{1,i}-P_{0,i}\right)=\alpha \frac{{w^{\prime }}_{1,i}}{{w^{\prime }}_{0,i}}\left({P^{\prime }}_{1,i}-P_{0,i}\right)$ (10)

其中，w和 $w^{\prime }$ 分别表示两个曲面上的权值， $P_{1,i}$ 、 $P_{0,i}$ 和 ${P^{\prime }}_{1,i}$ 分别表示B¹和B¹、B²公共边界以及B²内部控制点， $\alpha$ 为连续性系数。

求解得到NURBS曲面拼接G¹连续条件之后，将其作为约束用于实现G¹连续优化算法的设计。

3.3. 构建优化问题

根据两个NURBS曲面拼接G¹连续性条件设计其拼接处连续性优化算法，由于NURBS曲面的连续性与其控制点、权值和节点矢量相关，为了使优化算法更加简洁。采用两个曲面次数和节点矢量都相同，因此可以确定G¹连续性优化变量：控制点和权值。

根据控制点和权值的变化，为了实现G¹连续拼接，并且能够最小化控制点与权值的变化保证NURBS曲面网格质量，可以采用最小二乘法将控制点和权值的乘积设置优化约束目标。通过将G¹连续性条件作为约束，连续性系数设为1，可以得到其优化项：

$\min {\displaystyle \underset{j=1}{\overset{n-1}{\sum }}\left({\Vert P_{1j}{\omega }_{1j}-{\bar{P}}_{1j}{\bar{\omega }}_{1j}\Vert }^2+{\Vert {P^{\prime }}_{1j}{{\omega }^{\prime }}_{1j}-{{\bar{P}}^{\prime }}_{1j}{{\bar{\omega }}^{\prime }}_{1j}\Vert }^2\right)}$ (11)

其中， ${\bar{P}}_{1j}{\bar{\omega }}_{1j}$ 、 ${{\bar{P}}^{\prime }}_{1j}{{\bar{\omega }}^{\prime }}_{1j}$ 表示优化前控制点和权值的乘积， $P_{1j}{\omega }_{1j}$ 、 ${P^{\prime }}_{1j}{{\omega }^{\prime }}_{1j}$ 表示优化后控制点与权值的乘积。

根据公共拼接处的曲面控制点与权值的关系可以得到上述优化项满足的约束条件为：

$2P_{0j}=P_{1j}+{P^{\prime }}_{1j}$ (12)

综合其优化项以及约束条件可以采用拉格朗日乘子法进行求解，其中 $\lambda$ 是拉格朗日乘子：

$L={\displaystyle \underset{j=1}{\overset{n-1}{\sum }}\left({\Vert P_{1j}{\omega }_{1j}-{\bar{P}}_{1j}{\bar{\omega }}_{1j}\Vert }^2+{\Vert {P^{\prime }}_{1j}{{\omega }^{\prime }}_{1j}-{{\bar{P}}^{\prime }}_{1j}{{\bar{\omega }}^{\prime }}_{1j}\Vert }^2\right)}+{\displaystyle \underset{j=1}{\overset{n-1}{\sum }}{\lambda }_j}\left(2P_{0j}-P_{1j}-{P^{\prime }}_{1j}\right)$ (13)

4. 实现G¹连续的优化问题求解

4.1. 算法设计

NURBS面片在拼接时，需要确定每一片上需要优化的控制点，以方便进行迭代优化，选择迭代停止条件为： $O\left(n\right)\le 1.0\times {10}^{-3}$。

根据公式设计NURBS曲面G¹拼接优化算法：

Step 1. 输入两片NURBS曲面，搜索两曲面重合的部分，即：实现C⁰连续的公共控制点记为，并存储到容器中记为 $P_{0j}$，然后遍历两片的边界控制点分别记为 $P_1$ 、 $P_2$ ；

Step 2. 根据 $P_1$ 、 $P_2$ 之间的关系确定，两片NURBS曲面拼接的边是：u边、v边、u的对边还是v的对边；

Step 3. 确定两曲面分别再u、v方向上控制点的个数，分别记作a、b，计算 $P_1$ 、 $P_2$ 与控制点个数之间的关系，找到其内部控制点存入到容器中，分别记作 $I_1$ 、 $I_2$，并将其相邻控制点作为边界条件；

Step 4. 根据目标函数，以及等式约束条件，采用拉格朗日乘子法计算优化后的两片NURBS上的控制点和权值，并将其存入到容器中；

Step 5. 将优化后的控制点和权值大小带回到原曲面实现G¹连续拼接。

4.2. 求解结果

利用C++和QT实现上述算法，如下图3所示是双片NURBS曲面拼接时，利用优化思想得到的模型图。利用paraview进行雅可比数值的显示可以得到实现C¹/G¹连续前后的对比图，根据图片可以得到其再利用算法优化后，连续性得到明显的提升。

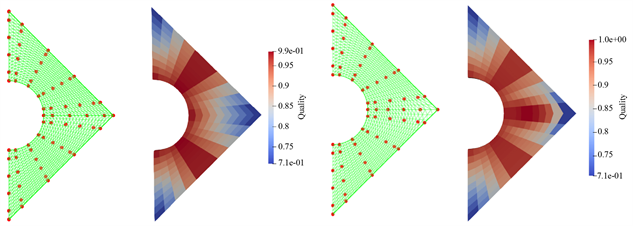
Figure 3. G¹ Comparison before and after continuous optimization

图3. G¹连续优化前后对比

根据图中可以看出优化前模型在拼接处的雅可比值偏低，该模型在进行等几何分析时会出现分析效果不理想的情况。经过优化后的模型在拼接处的雅可比值明显得到提升，更加符合等几何分析要求，在拼接处也更加连续。

5. 结论

目前B样条表达的模型在连续性上的研究比较成熟，但对于NURBS曲面上连续性拼接研究却比较少。本文设计一个对双片NURBS曲面在拼接处，实现G¹连续拼接优化的算法，该方法再保证曲面拼接C⁰连续的基础上，进一步优化控制点和权值使其变化量尽可能小，从而保证曲面形状不会发生改变；既能保证曲面拼接更加光滑，还能防止曲面出现因优化出现变形错位的情况；采用优化方式的NURBS曲面，其模型质量也更好，更适用于分析。目前，文章只针对二维NURBS曲面拼接，对于三维情况没有涉及。因此，本文的工作对于未来不同次数、不同节点矢量的NURBS曲面拼接以及NURBS体拼接具有一定的启发意义。