1. 引言
折射率是反映透明、半透明液体光学性质的重要参量之一,借助折射率可以探索液体的光学性能 [1] 、浓度 [2] 、成分 [3] [4] 等,在食品、化工、制药、光学等诸多工业领域和科研领域有着非常重要的应用。目前常用的液体折射率测量方法主要有阿贝折射仪法 [5] 、分光计法 [6] 、迈克尔逊干涉法 [7] ,以及马赫–曾德尔干涉法 [8] 等,采用上述方法虽然能精确地测量液体折射率,但测量仪器或操作步骤通常较为复杂,对于液体折射率的且部分测量方法的实验场景受限。
为简化液体折射率的测量、适应多样化实验环境,本文介绍了一种基于MATLAB图像处理简易测量液体折射率的方法。该方法是基于物体浸入盛有透明液体的烧杯中时,物体会按一定比例放大的现象来实现液体折射率的测量。粗细均匀的圆柱形细棒斜放入盛有透明液体的烧杯内,对该装置正面拍照,然后借助MATLAB对图片进行处理提取细棒轮廓,经由算法处理最终精确得到透明液体的折射率。
2. 实验原理
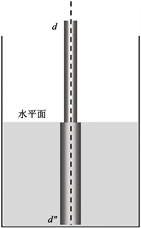
根据文献 [9] ,采用“测距法”可以推导出透明液体的折射率。但在实验过程中,使用的细棒密度有一定的要求,即浸入液体时不能使底部悬浮,同时对观察者的观察角度以及细棒的移动速度均做出了限制,这些因素极大的增加了实验的不确定性,且降低了实验结果的准确性。图1(a),图1(b)两图为“测距法”的原理示意图,(c)为本文所述方法的装置放置原理示意图。其中,烧杯内盛装的透明液体折射率记为n,透过烧杯观察到的水平面上部分细棒的直径均记为d,水平面下部分细棒直径分别记为
、
和
。
 (a)
(a) 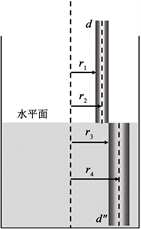 (b)
(b)  (c)
(c)
Figure 1. The experimental schematic diagram of “ranging method”
图1. “测距法”实验示意图
图1(b)即为文献 [9] 中所指的“折断”时刻,此时细棒的左端和中心相对于初始图(a)的轴线位置移动距离分别记为r1、r3和r2、r4。处于水平面以下部分的细棒直径可以描述为
(1)
并且有
,进一步推导得液体折射率为
(2)
相较于文献 [9] 中推导的透明液体的折射率公式,式(2)所推导出的求解公式与烧杯的直径无关,需要测量的物理量仅为细棒左端距离初始状态中心位置的距离r1和透过烧杯观察水平面上细棒的直径d。然而,在实际测量过程中,准确测量上述的r1具有很大的困难。因此,式(2)所提供的折射率计算方法实际操作难度较大,需要进行新的测量方法探索。
为解决上述问题,降低实验难度,需要对细棒的移动过程进行进一步分析。在细棒从图1(a)所示状态向图1(b)所示状态过渡过程中,水平面上部分均存在
(3)
且在图1(b)所示的“折断”状态下
(4)
将式(3)~(4)与式(1)联立,可以进一步推导出在移动过程中的任何时刻均存在
(5)
以上推论可以等效为:当细棒以图1(a)所示状态沿直径方向移动时,水平面以下的直径不随移动距离发生改变。
基于上述推论可以进一步得出,细棒沿着烧杯直径方向斜放入时,即图1(c)所示状态,视觉上水平面下各处细棒的直径相等。借助式(5)不难得出,水平面下细棒的直径为水平面上细棒直径的n倍。至此,烧杯中透明液体的折射率便仅与图1(c)状态下水平面上下细棒的直径相关
(6)
至此,在“测距法”的基础上探索出了液体折射率的新的表述方式,即当细棒以图1(c)所示状态沿径向方向放置于盛有透明液体的烧杯中时,沿垂直该直径方向记录下视觉上水平面上下细棒的直径,液体折射率便可以用下直径与上直径之商来描述。
3. 算法设计与实现
3.1. 图片采集及预处理
本实验所需器材为:透明烧杯,透明待测液体,红色均匀细棒。
依据图1(c)所示状态搭建实验器材,为精确得到透明液体的折射率,细棒颜色规定为红色。完成仪器搭建后,进行如图2所示的实验图片的采集。图2中(a)所示的透明液体为清水,(b)所示的透明液体为花生油,(c)所示的透明液体为浓度为53%的白酒。每种透明液体采集多组图片。
 (a) 清水
(a) 清水  (b) 花生油
(b) 花生油  (c) 白酒
(c) 白酒
Figure 2. Experimental pictures
图2. 实验图片
结合式(6)所推导出的液体折射率的表达式可知,在采集到的原始图片中,对于计算液体折射率有效的部分仅为图片中的红色均匀细棒。因此,首先需要对收集到的实验图片进行预处理,尽可能的保留细棒而过滤掉其他部分。实验图片的预处理进一步滤除掉其他部分对于后续算法设计的干扰,提高测量精度。
预处理过程主要分为以下三步:其一,充分利用细棒颜色进行细棒提取,将实验图片导入MATLAB并转化到HSV空间,确定红色细棒的颜色分布,并根据红色分量的取值范围进行细棒的分割提取。其二,利用graythresh函数实现基于最大类间方差法的图片阈值寻找,并借助该阈值将其转化为二值图像,此时得到的二值图像中,仍存在一部分背景噪声,借助图像形态学闭运算进行噪声去除,同时利用bwareaope函数对面积较大的噪声进行去除。其三,借助边缘检测算法进行细棒轮廓的提取,同时,鉴于本实验提取轮廓的关键在于得到细棒中的直径信息,因此还可以利用Hough变换和LSD算法进行细棒轮廓的提取。
3.2. 算法流程设计
图2所示的实验图片经过预处理后,得到关键部分——细棒轮廓。对多组经过预处理后的实验图片进行分析,不同图片中细棒所处的位置、细棒可用于直径提取的稳定区域以及区域的长度等都有较大的差异,而水平面的位置却有相似的规律。因此,在得到细棒轮廓图后,以水平面为切入点,首先确定轮廓图内水平面所在的位置,而后借助细棒端点以及水平面位置确定细棒上下直径的提取区域,最后在区域内采用改进的欧式距离法进行直径求解,继而得到液体折射率。
算法设计的详细流程如下:
1) 确定轮廓所在区域。在得到的轮廓图中,首先确定细棒轮廓在图中的位置,由于轮廓图为二值图像,因此基于find函数可以实现对细棒轮廓所有像素点的提取,同时对应于笛卡尔坐标系转化为坐标点。在此基础上确定细棒轮廓在y轴方向上边界点ymin、ymax,锁定纵向有效区域。
2) 得到细棒轮廓的变化矩阵。遍历[ymin, ymax]中的所有y值,对于每一个y值,找出轮廓上取该y值的所有x值并计算一阶差分,此时,一阶差分的最大值代表该位置上细棒左右两端的相距的距离,故而将所有每一个y对应位置上的一阶差分最大值取出组成过渡矩阵。当细棒轮廓上纵向相邻位置的棒距差距过大,一般将该位置对应于水平面或细棒上下端点。因此对过渡矩阵进行一阶差分得到变化矩阵,显然变化矩阵中的峰值包含有水平面及细棒上下端点信息。
3) 确定水平面位置。在实际操作中,变化矩阵的峰值中还包括噪声,实际的变化矩阵在水平面处不是仅存在唯一峰值,而是一系列峰值组成的一小段区间。基于tabulate函数快速统计变化矩阵各数出现的频率,将出现概率低于30%的数认定为尖峰,并将其最小值作为阈值,利用峰值函数findpeaks确定这些尖峰出现的位置。本实验图片中水平面位于烧杯中点附近,故而位于[ymin, ymax]中点附近的一簇尖峰即为水平面所在的区间。
4) 确定水平面上下直径待选取区域。细棒上端点与水平面间的区域为水平面上细棒直径的提取区域,考虑到噪声的影响,变化矩阵中靠近ymin的一簇尖峰记为细棒上端点区域。因此上端点区域的下界与水平面区域的上界组成的区域为细棒上直径的提取区。为保证实验精度降低误差,该提取区的上下界均需要去掉一段调节阈值。采用同样的方法确定细棒下直径的提取区。
5) 随机选取子区域。在步骤4提供的上下待选区域内分别随机选取一小段区域作为实际的直径提取区域。
6) 子区域内求解直径。在确定的子区域内依次遍历细棒左端每一个轮廓点,并计算该点与此子区域内细棒右端每一个轮廓点的欧式距离,根据直径的定义,欧式距离的最小值即为该子区域内的细棒直径。
7) 基于子区域的液体折射率求解。依据步骤6求解各子区域内水平面上下细棒的直径,并带入公式(6)得到液体的折射率。
8) 迭代求解精确液体折射率。步骤5~7迭代100次,记录每一次的折射率值,并将其平均值作为该透明液体最终的折射率。
算法步骤如图3所示。
3.3. 算法实现
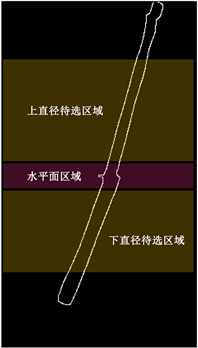
图4(a)中的白色细棒轮廓即为图2(a)经过预处理后得到的图片。图4(b)则是由细棒轮廓信息进一步得到的变化矩阵信息,其中,横坐标对应于轮廓上每一个点在纵向上的位置关系,纵坐标对应于变化矩阵。通过算法步骤(1)确定了图4(a)中细棒轮廓所处的区域[2, 952],经由步骤(2)得到了如图4(b)所示的变化矩阵图,在得到变化矩阵以及轮廓所在区域后,通过步骤(3)确定出水平面所在的区域为[532, 548],接着便可以确定出水平面上下直径待选取区域。
 (a)
(a) 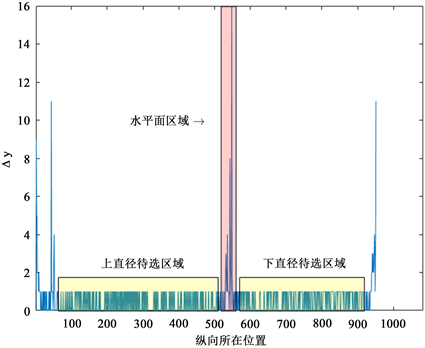 (b)
(b)
Figure 4. The horizontal plane and the area above and below the horizontal plane can be used for diameter extraction.
图4. 水平面及水平面上下可用于直径提取的待选区域
完成直径待选区域范围的确定后,为进一步提高检测精度,减小误差,在待选区域给定的范围内进行小区域随机选取及多次迭代。确定最大迭代次数100,每次迭代时用unifrnd函数随机选取子区域,采用步骤(6)所述方法计算该区域内细棒直径,同时记录该次所得的液体折射率。当达到最大迭代次数100后,对于迭代中得到的所有液体折射率取平均值作为该液体的折射率。
4. 结果分析
图片预处理的好坏对于液体折射率的精度存在影响。在采集到如图2所示的实验图片后,预处理得到细棒轮廓有以下四种方法:基于Canny算子的轮廓检测 [10] ,基于Log算子的轮廓检测 [11] ,基于Hough变换的轮廓提取 [12] ,基于LSD算法的轮廓检测 [13] 。分别采用上述四种预处理方法处理图2的实验图并进行液体折射率的计算,同时对比相关文献测量值 [14] [15] [16] ,结果如表1所示

Table 1. Comparison of refractive index results obtained by four pretreatment methods (temperature: 20˚C)
表1. 四种预处理方法所得的折射率结果对比(温度:20℃)
由表1,采用直线检测算法的Hough变换和LSD算法预处理后得到的折射率值误差较大,采用边缘检测算法的两种方法中,基于Canny算子的轮廓检测所得结果最接近理论值,准确度最高。
基于上述方法对于同一液体所采集的不同实验图片进行多次折射率的计算。常见的三种透明液体:清水、花生油、53度白酒,采用本文所述方法得到的折射率如表2所示。

Table 2. Liquid refractive index based on Canny operator (temperature: 20˚C)
表2. 基于Canny算子的液体折射率(温度:20℃)
为进一步评估实验结果的精度,本文引入均方误差MSE
(7)
其中,将每幅实验图片的计算值作为估计值xi,文献值作为真值u,参与实验的图片共N幅,把表2中三种液体的实验数据分别代入式(7),得到清水、花生油和53˚白酒的均方误差依次为2.125 × 10−7,1.19 × 10−6,3.38 × 10−6。均方误差反映了实验数据的离散程度,由此,采用本文所述方法得到的实验结果精确度高。
三种透明液体的平均相对误差分别为0.02%,0.13%、0.06%。相较于无色透明液体清水和白酒,呈淡黄色的花生油的平均相对误差偏大,有色透明液体对于算法检测的准确度造成了一定干扰。因此,针对有色透明液体的检测,可以尝试更换均匀细棒的颜色或更换到其他颜色空间对实验图片进行预处理等方式改善测量精度。总体而言,采取本文所述方法测量透明液体的折射率均方误差小,精度高,平均相对误差均小于0.15%,准确度高,充分证明了该方法的可行性、科学性。与传统的测量液体折射率的方法相比,该方法设备简单易得、结果精度高,实验过程无污染。
5. 结论
本文提出一种基于数字图像处理测量透明液体的折射率方法。在图像预处理过程中,比较了基于Canny算子、Log算子、Hough变换和LSD算法的轮廓检测效果,结果表明基于Canny算子的轮廓检测所得结果准确度最高。利用该方法测量了20℃下三种常见透明液体清水、花生油和53°白酒折射率,结果表明测量折射率的相对误差小于0.15%。基于本文的液体折射率测量法设备简便易得,可操作性强,结果精度及准确度高,有很好的实用价值。
致谢
感谢三峡大学理学院实验中心对实验的大力支持,同时感谢湖北省教学研究项目的资金支持。
基金项目
湖北高校省级教学研究项目(项目编号:2020378)。
NOTES
*通讯作者。