基于WGAN状态重构的智能电网虚假数据注入攻击检测

Detection of False Data Injection Attack in Smart Grid Based on WGAN State Reconfiguration

摘要: 针对虚假数据定位检测适应性低、篡改量测影响系统状态精确感知的问题，提出一种基于WGAN (Wasserstein generative adversarial networks, WGAN)状态重构的智能电网虚假数据检测与修正模型。首先，根据历史状态变量的概率分布，初步锁定并剔除具有潜在攻击风险的状态变量。然后，采用Wasserstein生成对抗网络重构缺失变量，WGAN通过Wasserstein距离衡量生成分布与真实分布之间的差异，能够生成有意义的梯度以优化网络模型参数。最后，以重构状态作为一种状态参考，精确定位攻击节点，并结合网络拓扑参数修正篡改量测值。将纽约州数据用在IEEE-14节点测试系统，进一步验证所提方法的可行性与有效性。

Abstract: Aiming at the problems of low adaptability of false data location detection and the influence of tamper measurement on the accurate state awareness for the power system, a false data detection and correction model of smart grid based on state reconstruction of Wasserstein Generative Adver-sarial Networks (WGAN) was proposed. Firstly, the state variables with potential attack risk are ini-tially locked and eliminated according to the probability distribution of historical state variables. Then, the missing state variables are reconstructed by Wasserstein generative adversarial net-works. WGAN measures the difference between the generated distribution and the real distribution through Wasserstein distance, which can generate meaningful gradients to optimize the parame-ters of the network model. Finally, the reconstructed variables are used as a state reference to lo-cate the attacked bus, and to correct the measurement data combined with the network topology parameters. The feasibility and validity of the proposed method are further verified in IEEE-14 bus test system with the New York data.

1. 引言

随着电力物理系统与信息系统深度耦合，智能电网可观测性显著增强，但也面临网络安全的威胁 [1] [2] 。虚假数据注入攻击(false data injection attacks, FDIA)作为智能电网中兼具破坏性与隐蔽性的网络攻击 [3] ，通过篡改电力量测数据，使状态估计失去对系统状态的准确感知，引起能源管理系统(energy management system, EMS)做出错误决策，进而破坏电力系统安全稳定运行 [4] 。因此，研究高效FDIA检测与修正方法对保障智能电网安全性、可观测性具有重要意义。

现有文献针对FDIA的防范研究主要集中在物理防御与在线检测两个方面。物理防御专注加密一组现有量测或优化配置向量测量单元(phasor measurement unit, PMU)，防范电力量测数据遭到篡改。文献 [5] 通过图形分析法加密最优量测子集，遏制FDIA。文献 [6] 以PMU绝对安全为前提，采用贪婪算法确定PMU最佳位置防范FDIA。然而，文献 [7] 指出物理防御无法确保加密量测或PMU绝对安全，加密设备的高额资金也限制了在大型电网中实际应用。为此，基于数据的在线检测方法被提出并持续改进。统计学方法最先用于FDIA检测，文献 [8] 通过计算攻击前后量测变化概率分布之间的KLD (Kullback-Leibler divergence)进行检测，但面对数据的激增、攻击方式的演变呈现局限性。而深度机器学习具有出色的从大数据中提取特征的能力，文献 [9] 利用改进的卷积神经网络，识别虚假数据的行为特征，提高分类检测精度。

上述研究集中于检测攻击存在与否，根据实际电力系统的安全要求，需进一步识别攻击节点与受损量测，为EMS操作人员隔离攻击节点、执行量测物理保护提供必要的数据支撑。文献 [10] 采用基于机器学习的一类一网检测模型为小节点系统每个节点构建分类检测器，在节点数量众多的大型电力系统复杂性增加。文献 [11] 将发电机的输出功率视为绝对安全序列，通过维特比算法预测状态值作为参考，识别攻击节点。这种方法的适用性增强，但对低强度的节点状态值攻击，检测率不理想。为进一步提高攻击节点检测精度，文献 [12] 基于自适应无迹卡尔曼滤波算法估计系统状态，经一致性检验、虚假数据隐蔽性检验，提升识别率。估计算法假设噪声符合正态分布、量测误差为常数阵，与实际电网噪声时变性、量测误差在不同节点、不同线路存在差异性不相符，影响状态预测精度，进而影响攻击识别率。

生成对抗网络(generative adversarial networks, GAN)因能充分学习复杂数据之间的分布规律，已被用于电网不同类型量测缺失重构工作。文献 [13] 利用无监督GAN自主提取数据特征，并结合双重语义感知重构约束，使高比例有功量测缺失重构精度达100%。文献 [14] 以Wasserstein距离代替JS散度，采用WGAN克服了GAN训练过程导致的梯度消失问题，通过真实性约束、上下文约束挑选最优生成量测，随机缺失量测重构误差低于7.0 e⁻⁴pu。而高精度随机数据缺失重构的实现，契合局部网络拓扑结构下随机节点状态受到攻击的问题，为从状态重构角度建模，解决定位检测模型中状态预测精度低、节点分类器适应性受限的问题，提供了理论依据。

因此，本文利用WGAN重构精度高的优势，提出一种基于状态变量重构的智能电网虚假数据检测与修正模型。根据历史状态变量的概率分布，采用“3σ”准则锁定并剔除具有潜在攻击风险的状态变量；WGAN通过Wasserstein距离对状态变量进行无监督重构训练，使生成器模型具备快速重构出接近真实状态值的能力；将生成器重构的状态值作为一种状态参考，定位攻击节点并替换受损状态，结合网络拓扑参数修正篡改量测值。算例仿真验证所提方法的有效性。

2. 虚假数据基本原理

2.1. 状态估计与不良数据检测

在电网中，控制中心通过状态估计，利用实时量测系统的冗余性提高数据精度，自动消除随机干扰引起的误差信息 [15] 。电力系统状态估计是通过各种智能仪表的监测数据，对当前系统运行状态评估的过程。其结果常用于经济调度、安全评估等。在交流状态估计模型中，给定量测数据z，通过求解最小化目标函数，计算系统状态值x。

$J\left(x\right)={\left[z-h\left(x\right)\right]}^{\text{T}}{R}^{-1}\left[z-h\left(x\right)\right]$ (1)

式中，z为包含电压幅值、节点注入功率、线路传输功率的量测向量；x为包含节点电压幅值、电压相角的系统状态变量；h(x)为量测向量与状态变量的非线性函数；R为已知量测误差方差阵。

为发现因通信干扰、仪表故障可能导致的量测异常，传统不良数据检测机制通常基于残差r欧几里得范数 ${\Vert r\Vert }_2$ 与预定检测阈值 $\tau$ 比较，大于阈值 $\tau$ 表明存在不良数据。残差定义为：

$r=z-h\left(x\right)$ (2)

2.2. 局部虚假数据注入攻击数学模型

攻击者在掌握电力系统网络拓扑参数并能同时篡改多个量测的情况下 [16] ，设攻击受损量测为 $z_a$ ，攻击后状态变量为 $x_a$ 。此时，残差公式为：

$\begin{array}{c}{r}_a={\Vert z_a-h\left(x_a\right)\Vert }_2\\ ={\Vert z+a-h\left(x+c\right)\Vert }_2\\ \le {\Vert z-h\left(x\right)\Vert }_2+{\Vert a-h\left(x+c\right)+h\left(x\right)\Vert }_2\\ ={\Vert r\Vert }_2+{\tau }_a\end{array}$ (3)

式中，a为攻击向量；c为由攻击后状态偏差向量； ${\tau }_a$ 为由攻击引起的残差增量值。

由公式(4)知，当攻击向量满足

$a=h\left(x+c\right)-h\left(x\right)$ (4)

由攻击引起残差增量 ${\tau }_a$ 为0，使得 $r_a={\Vert r\Vert }_2$ ，即可实现攻击的隐蔽性。

由公式(4)可知，攻击者掌握电网全部拓扑信息下的攻击成功率更高，但掌握局部信息，使局部节点状态受损的攻击更符合实际 [17] 。针对局部区域节点i的电压幅值攻击为例，局部攻击向量a中节点有功注入增量 $\Delta P_{ia}$ 、节点无功注入增量 $\Delta Q_{ia}$ 为：

$\Delta P_{ia}={\displaystyle \underset{j\in {\Omega }_i}{\sum }{V}_j\left[G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij}\right]}\left[-V_i+\left(V_i+\Delta V_{ia}\right)\right]$ (5)

$\Delta Q_{ia}={\displaystyle \underset{j\in {\Omega }_i}{\sum }{V}_j\left[G_{ij}\sin {\theta }_{ij}-B_{ij}\cos {\theta }_{ij}\right]}\left[-V_i+\left(V_i+\Delta V_{ia}\right)\right]$ (6)

式中，V_i、V_j分别为节点i、节点j的电压幅值； ${\theta }_{ij}$ 为节点i与节点j的电压相角差； $\Delta V_{ia}$ 为节点i的电压幅值攻击增量；G_ij、B_ij分别为节点i与节点j之间支路电导、电纳； ${\Omega }_i$ 为节点i与相连节点构成的电力节点集合。

3. 基于WGAN状态重构的攻击检测模型

3.1. 基于WGAN的状态重构

GAN以JS散度作为损失函数衡量生成分布与真实分布的差异，面临两种分布没有重叠部分时，损失函数突变常值导致梯度消失。WGAN以Wasserstein距离代替JS散度，即使两种分布没有重叠，Wasserstein距离依旧平滑变化，生成有意义的梯度以优化网络模型参数，克服GAN训练过程中梯度消失问题 [14] 。

WGAN由相互博弈的生成器与判别器两个对抗网络构成。从历史数据库选取m组无缺失状态变量构建数据集 $X={\left\{x_i\right\}}_{i=1}^m$ ，样本数据 $x_i=\left[V_i,{\theta }_i\right]$ ，设无缺失样本数据 $x_i$ 之间复杂分布规律为 $p_r\left(x_i\right)$ 。构建与样本数据 $x_i$ 维度一致的随机二值掩码矩阵M，其中0代表随机缺失状态，1代表未缺失部分。为改善重构效率，将样本数据 $x_i$ 与M做哈达玛积(Hadamard product)运算，构成随机缺失 ${x^{\prime }}_i$ 作为生成器的输入 [18] ，通过生成器和判别器构建 $p_r\left(x_i\right)$ 与重构状态 $p{}_g\left({x^{\prime }}_i\right)$ 之间的映射关系。训练过程如图1(a)所示。

重构检测阶段，针对t时刻状态变量 $x_t$ 存在潜在攻击风险状态变量 $x_s$ 情况，剔除 $x_s$ 后，将缺失状态变量 ${x^{\prime }}_t$ 送入训练完成的生成器模型，重构完整状态量 $G\left({x^{\prime }}_t\right)$ ，重构过程如图1(b)所示。

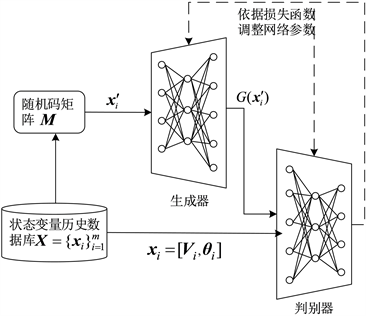(a) 模型训练(b) 状态重构

Figure 1. State reconstruction basic structure based on WGAN

图1. 基于WGAN的状态重构基本框架

3.2. WGAN网络结构

生成器网络结构如表1所示，由4层卷积网络组成，不仅对状态变量进行特征提取，也确保输入与输出维度一致。卷积后添加批标准化层保证模型的非线性表达能力，使梯度传播层次更深 [19] 。卷积之后采用Tanh激活函数，输出14 ´ 2 ´ 1的重构状态变量。

Table 1. Parameters of generator network of WGAN

表1. WGAN生成器网络参数

判别器网络结构参数如表2所示。判别器输入为生成器生成样本 $G\left({x^{\prime }}_i\right)$ 和真实样本 ${x^{\prime }}_i$ ，网络结构类似于生成器的镜像。经过3层卷积特征提取后，Flatten函数在不改变卷积层输出顺序的情况下将数据进行降为压平。最后由全连接层与sigmoid 函数输出属于真实状态变量的概率。

Table 2. Parameters of discriminator network of WGAN

表2. WGAN判别器网络参数

3.4. 虚假数据检测与修正流程

FDIA检测模型涉及潜在风险状态变量锁定、虚假数据隐蔽性检验，以及检测准确率指标。

1) 采用“3σ”准则锁定潜在攻击风险状态变量，公式如下：

$\left|x_t-x_{t-1}\right|>\left|\mu \pm 3\sigma \right|$ (7)

式中， $x_t$ 为t时刻状态变量， $\mu$ 、 $\sigma$ 分别为依据历史数据库计算状态变量变化量的均值、方差向量。

2) 虚假数据隐蔽性检验公式如下：

$return\left(\left|x_s-x_r\right|\ge {\tau }_1\Vert {\tau }_2\right)$ (8)

式中， $x_s$ 为锁定的潜在攻击风险状态变量； $x_r$ 为生成器重构的攻击风险状态变量； ${\tau }_1$ 、 ${\tau }_2$ 分别为攻击检测电压幅值阈值、相角阈值； $return(\cdot )$ 为返回满足括号内条件向量元素的索引。

3) 采用检测准确率、查全率衡量模型性能，公式如下：

$A_c=\frac{TN+TP}{TN+FN+TP+FP}$ (9)

${\eta }_r=\frac{TP}{FN+TP}$ (10)

式中，TN为正常样本识别为正常的数量；FP为正常样本识别攻击的数量；FN为攻击样本识别为正常的数量；TP为攻击样本识别为攻击的数量。

基于状态重构虚假数据检测与修正模型流程如图2所示，主要包含以下4个步骤。

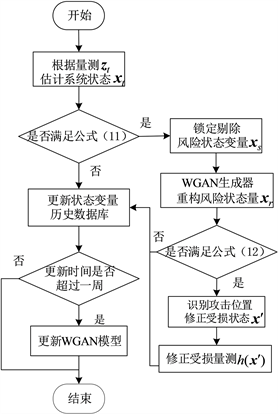
Figure 2. Flow chart of examine model against false data

图2. 虚假数据检测与修正模型流程图

1) 根据系统获取的量测量，估计系统运行状态，采用公式(7)锁定是否具有潜在风险状态量。

2) 针对潜在风险状态变量，剔除后由WGAN生成器模型重构潜在风险状态估计值，并采用公式(8)定位识别节点是否受到攻击。

3) 受损状态值由重构值替换，构成状态修正量 $x^{\prime }$ ，结合网络拓扑参数修正受损量测 $h\left(x^{\prime }\right)$ 。

4) 为充分学习状态变量随时间的变化规律，状态变量历史数据库保留一个月状态变量，每周更新一次基于WGAN状态重构的生成器模型。

4. 算例分析

在IEEE14节点系统中验证所用模型的有效性，系统网络拓扑结构如图3所示。MATLAB和MATPOWER用于生成实验数据，WGAN模型使用python语言在pytorch环境下搭建，PC配置为I5-8300H/8GB RAM。

Figure 3. IEEE-14bus test system

图3. IEEE-14节点测试系统

4.1. 测试系统与模型训练参数

IEEE14节点测试系统采用全量测配置方式，其量测向量z包含节点注入有功量测14个，节点注入无功量测14个，20条支路有功量测40个、支路无功量测40个，节点电压量测14个，总计112个量测值。使用纽约独立系统运行商 [20] (New York independent system operator, NYISO)2020年1、2月份每5分钟的负荷数据模拟实际电力系统运行状况，状态数据的获取过程如下：

1) 将IEEE14节点系统的各个节点与纽约州11个地区的负荷匹配连接，匹配关系矩阵如下：

$\left[\begin{array}{ccccccccccc}2& 3& 4& 5& 6& 9& 10& 11& 12& 13& 14\\ 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11\end{array}\right]$

矩阵第一行代表IEEE-14的节点编号，矩阵第二行为相应的NYISO地区编号。

2) 将纽约州11个地区负荷数据标幺化到与之对应的IEEE-14节点，初始化有功负荷和无功负荷，使测试系统运行在IEEE-14节点初始状态附近。由于NYISO没有提供无功负荷，假设测试系统负荷具有恒定的功率因数，计算得到节点无功负荷。

3) 假设发电机发电量与系统总负荷增速相同，计算新的系统总负荷与系统初始总负荷的比值，乘上系统所有发电机的出力。

4) 每隔五分钟通过MATPOWER潮流分析，将潮流计算值作为系统的量测真值，并在量测真值基础上添加均值为0，标准差为0.01的高斯噪声，得到量测值。

5) 对收集的量测值送入控制中心，估计系统运行状态，并进行不良数据检测。

训练WGAN时，将历史数据库1月份前30天状态数据按9:1划分训练集X_train和测试集X_test，X_train维度为(7776，14 × 2)，X_test维度为(864，14 × 2)。设训练迭代次数epochs为100，批处理量batchsize为64，生成器学习率为0.00005，判别器学习率为0.00005。

4.2. 局部虚假数据构建分析

为验证虚假数据构建的有效性，模拟IEEE-14节点系统的局部区域有限节点受到攻击的场景。假设攻击者掌握电力系统局部网络拓扑结构，并具备篡改局部区域相关量测的能力。以图3的攻击区域为例，假定攻击后节点2的电压幅值偏差增量 $\Delta V_{2a}$ 为−0.047，节点3的电压幅值偏差增量 $\Delta V_{3a}$ 为0.037，基于式(4)构建针对 $V_2$ 、 $V_3$ 攻击向量a的非零元素值，局部网络拓扑下的量测参数的变化见表3。

Table 3. IEEE-14 bus system local attack measurements

表3. IEEE-14节点系统局部攻击量测数据

将攻击向量a叠加在量测向量z形成虚假数据 $z_a$ 送入控制中心进行状态估计，图4为局部拓扑节点攻击前后电压幅值估计值、残差变化情况。

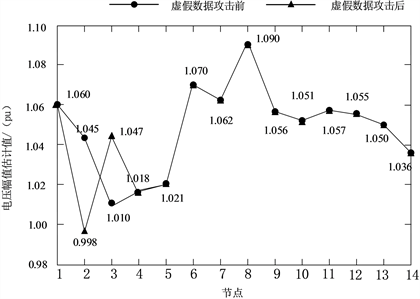(a) 攻击前后节点电压幅值估计值对比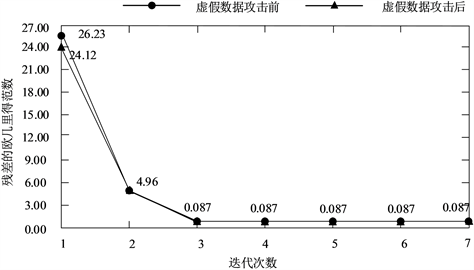(b) 攻击前后残差的欧几里得范数变化

Figure 4. IEEE-14bus system local false data attack effect

图4. IEEE-14节点系统局部虚假数据攻击结果

由图4可见：

1) $V_2$ 由原来的1.045降低为0.998， $V_3$ 由原来的1.010上升为1.047，而系统的残差值经多次迭代依旧为0.087，成功躲避不良数据检测机制，实现了局部攻击的隐蔽性。

2) 攻击者在掌握局部网络拓扑结构情况下，构建的电压幅值偏差增量 $\Delta V_{2a}$ 、 $\Delta V_{3a}$ 能准确干扰 $V_2$ 、 $V_3$ 到特定值，而不影响其他状态变量的变化。 $\Delta V_{2a}$ 、 $\Delta V_{3a}$ 的出现打破原状态变量的内部相关性，为从状态重构角度出发，实现定位检测，提供了理论依据。

4.3. 重构效果分析

WGAN模型训练完成后，在测试集中添加随机掩码矩阵N，设N中0代表随机缺失状态变量，1代表未缺失部分。在IEEE14节点系统中，随机设定缺失节点状态数据送入生成器模型中进行重构，测试系统节点状态数据在单节点缺失、多节点缺失情况下的绝对误差均值与重构平均时间。表4给出单节点状态缺失情况下不同节点电压幅值与相角的绝对误差均值。图5为多节点缺失情况下的绝对误差均值与重构平均时间。

Table 4. Reconstruction result of missing state of single node based on WGAN model

表4. 基于WGAN模型单节点缺失状态重构效果

由表4可见：

1) 单节点状态缺失情况下，电压幅值与相角重构误差低于量测误差，WGAN模型可为系统提供准确的状态值。

2) 电压幅值的重构效果要优于相角，其原因是负荷变化时，电力系统电压幅值的波动幅度相比于相角更加稳定。

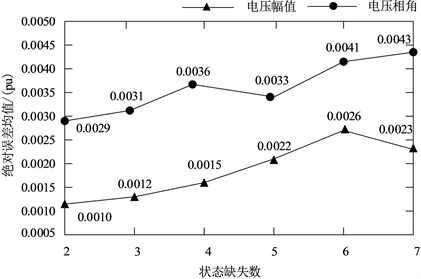(a) 多节点状态缺失的绝对误差均值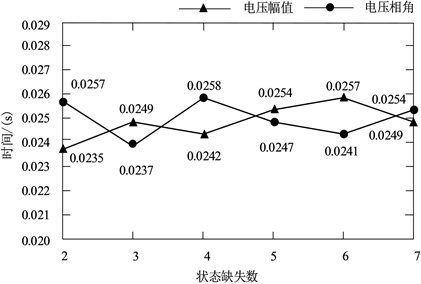(a) 多节点状态缺失的重构平均时间

Figure 5. WGAN multi-node missing reconstruction result

图5. WGAN多节点缺失重构效果

从图5中可见：

1) 当状态缺失数小于等于4时，电压幅值与相角的重构绝对误差均值波动较小，具有较为稳定的重构效果；随着缺失量的进一步增加，电压幅值与相角的绝对误差均值增长较快，但重构电压幅值绝对误差均值保持在0.003之下，重构相角绝对误差均值保持在0.005之下，WGAN模型具有较好的重构效果。

2) 不同缺失比列对状态重构的平均时间影响较小，重构平均时间在0.024s左右，重构效率得到保证。

3) 在状态缺失比列不断增大情况下，WGAN模型依旧能充分学习状态变量之间时空特征、相互性、周期性等变化规律，具备快速重构出接近真实状态值的能力。

4.4. 检测阈值设定

式(9)中攻击检测电压阈值t₁、相角阈值t₂选取的合理性直接影响检测结果的准确性。若阈值设定过低，未被攻击的节点将被判定为攻击；若阈值选取过高，攻击节点漏检的可能性增大。针对IEEE-14节点系统27个状态值模拟二月份第一周的单节点、多节点攻击，攻击状态偏差量c为正常状态变量的±10%、±5%，采用准确率、查全率作为阈值选取的调优指标，阈值调整对调优指标的影响如表5所示。

Table 5. Detection threshold adjustment based on accuracy and recall

表5. 基于准确率与查全率的检测阈值调整

从表中可见，随着检测阈值的增加，攻击检测的准确率缓慢上升，但查全率在电压阈值t₁取0.003、相角阈值t₂取0.0045时，呈明显下降趋势，表明随着阈值的增加，攻击漏检的情况显著增多。相比于将正常运行的节点判定为攻击，攻击漏检情况对系统的危害性更强。因此，设定电压阈值t₁为0.003、相角阈值t₂为0.0045，作为区分节点状态有无受到攻击的评判依据。

4.5. 攻击检测分析

为验证算法性能，将本文检测方法与深度卷积残差神经网络RestNet50、无迹卡尔曼滤波(unscented kalman filter, UKF)在单节点攻击时的对比见表6。另外，所提方法在多节点状态攻击检测结果见表7。

Table 6. False data single node attack detection result

表6. 虚假数据单节点攻击检测结果

由表6可见：

1) 基于WGAN状态重构的攻击检测模型针对单节点电压幅值不同强度攻击，其中最小准确率也在0.99之上，表明幅值攻击强度对检测模型影响较小。

2) 随着相角攻击强度的衰减，相比于电压幅值，攻击检测准确率略有下降，但整体检测准确率在0.98左右波动。其原因为攻击幅度较为接近原始值，且相同缺失比例下电压相角重构精度要低于幅值。

3) 相比RestNet50检测方法，本文检测方法凭借可靠的重构效果，整体准确率提升了6%左右。相比UKF检测算法，低强度的相角定位攻击检测准确率也保持在0.978之上，表明检测模型良好的稳定性与准确性。

Table 7. False data multi-node attack detection result

表7. 虚假数据多节点攻击检测结果

由表7可见：

1) 检测模型针对多节点电压幅值不同强度的攻击，检测准确率依旧在0.99之上，表明幅值攻击数量对检测模型影响较小。

2) 随着相角攻击数量的增加、攻击强度的衰减，检测准确率呈现明显下降趋势，其原因为相角缺失比例的增加，重构误差增大，定位所有相角攻击节点难度进一步增强。

4.6. 修正受损量测

针对多节点攻击，剔除全部虚假数据严重影响电力系统的可观测性。本文利用高精度的重构值替换受损状态，结合网络拓扑结构重新计算修正量测，为电力系统提供接近真实值的伪测量值。以 $\left({\theta }_5,{\theta }_9,{\theta }_{13}\right)$ 相角受到状态+5%攻击为例，修正各节点注入有功、节点注入无功如图6所示。从图中可得，利用重构状态 $\left({{\theta }^{\prime }}_5,{{\theta }^{\prime }}_9,{{\theta }^{\prime }}_{13}\right)$ 结合网络拓扑结构，所得修正量测与原始量测值吻合程度高，为系统可观测性提供数据支撑。

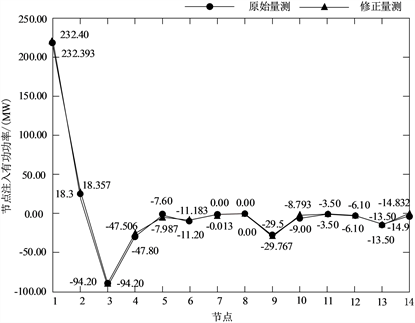(a) 节点注入有功功率修正(b) 节点注入无功功率修正

Figure 6. 3 node voltage phase Angle attack correction result

图6. 3节点电压幅值攻击修正结果

5. 结论

为实现虚假数据注入攻击的定位检测与受损量测值修正，提出一种基于状态重构的电力系统虚假数据注入攻击检测模型，并利用IEEE-14节点系统和NYISO发布的负荷数据进行仿真分析，研究结论如下：

1) WGAN模型对不同缺失比例状态变量能保证快速重构出接近真实值的状态值，对实现状态攻击检测、修正受损量测提供了稳定的状态参考。

2) 在IEEE-14节点系统中，检测模型针对单节点攻击具有较高检测准确率，有效遏制FDIA，确保电力系统安全稳定运行。

3) 在多节点攻击中，利用高精度的重构状态结合网络拓扑参数提供的修正量测值，确保系统的可观测性。

参考文献