2 K超流氦池压力控制的模拟与分析

Simulation and Analysis of Pressure Control in 2 K Superfluid Helium Pool

摘要: 超流氦因其优秀的热力学特性被广泛应用于国外大型超导加速器中。随着科学研究的发展，国内对超流氦的需求也有所提高。目前制备2 K超流氦的经典方法为抽气减压制冷技术，超导加速器对该过程中氦池的压力稳定性的要求不断提高，当前主流的压力控制手段已很难满足需求。本文提出一种基于热力计算的压缩机抽气量精确调节方法，结合氦的物性和氦池内的各物性参数建立控制方程。在MATLAB中对比普通的PID调节方法与该精确调节方法的压力波动表现，证明其提高压力稳定性的作用。

Abstract: Superfluid helium is widely used in superconducting accelerators due to its excellent thermody-namic properties. With the development of scientific research, the demand for superfluid helium in China has also increased. At present, the classic method for preparing 2 K superfluid helium is de-compression refrigeration technology. The requirements for the pressure stability of the helium pool in superconducting accelerators are constantly increasing, and the current mainstream pres-sure control methods are difficult to meet the requirements. This article proposes a precise ad-justment method for compressor suction based on thermal calculation, which combines the physical properties of helium and various physical parameters in the helium pool to establish a control equation. Comparing the pressure fluctuation performance of the ordinary PID adjustment method with that of the precise adjustment method in MATLAB, its role in improving pressure stability is demonstrated.

1. 引言

超流氦是一种特殊的冷却介质，具有低动力粘度、高导热率、高临界热流密度等独特的热力学特性，使其在大型超导加速器中被广泛应用于冷却超导腔及超导磁铁。早期大科学装置在饱和液氦的冷却下可以满足当时的研究需要。但随着高能物理技术领域的深入发展，对超导磁体装置提出了更高磁场和能量的要求，因此，在低温超导磁体的进一步开发中提出了对超流氦的应用 [1] 。目前，国外大型氦低温系统已普遍使用超流氦冷却，对大型氦制冷机及2 K系统的建造及运行具备了非常成熟的经验，具有稳定、可靠的工业化产品。在国内，科学研究的发展已经突显了对超流氦制冷的迫切需求 [2] 。

目前制备超流氦的经典方法为压缩机减压降温技术，即通过压缩机抽吸氦气，降低液氦槽内的饱和压力和饱和温度，从而获得超流氦。在超导加速器中的低温系统内，超导腔浸泡于超流氦池中，为冷量的消费终端。在实际的运行过程中，超流氦池的压力波动大小会严重影响超导射频腔的稳定运行，因此超流氦池的压力波动大小成为了设计超流氦池的重要指标之一。

当前主流的压力控制手段为增设辅助管路和缓冲罐等设备，通过PID控制调节对超流氦池内的补气、补液回路的阀门开度及压缩机的抽速，最终达到减小压力波动的目的 [3] 。然而，仅以压力为目标调节压缩机的转速，本质上是从控制的角度调节了抽气的体积流量，忽略了氦在低温下的实际物理状态变化以及氦池内的具体情况。鉴于此，本文拟建立超流氦池减压降温模型，结合MATLAB软件进行热分析，提出结合超流氦物理性质和氦池情况对压缩机抽速的精确调控方法。在此基础上，拟通过以传统PID调节抽速控制方法与该精确调控方法对比，验证该方法提高氦池压力波动稳定性的能力，进而为提高大型低温系统的压力稳定性提供理论基础。

2. 氦池降温系统热分析

2.1. 超流氦池系统结构

超流氦池的基本系统结构如图1所示，使用压缩机对2 K超流氦池进行抽气降压，由于超流氦及其上方氦气均为饱和状态，其饱和蒸汽压和温度具有单调关系，因此随着压力的降低温度也会降低 [4] 。由于抽气引起超流氦的蒸发，容器内超流氦的液位会随降温的进行逐渐降低。为保持液面高度的稳定，需要对氦池内的工质进行补充。为了提高超流氦池的压力波动可控性，直观对比冷压缩机主动调控能力，选择使用4.2 K冷箱中的4.2 K液氦进行补液，4.2 K氦气进行补气。

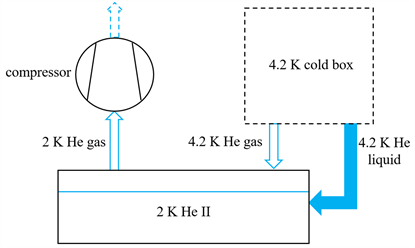
Figure 1. Structure diagram of superfluid helium pool system

图1. 超流氦池系统结构图

2.2. 传热理论计算

超流氦池工作的热力过程如图2所示，以容器内的超流氦及其上方的氦气为控制系统，系统内的传热传质过程主要包括进入超流氦贮存容器的补充氦气 ${\stackrel{\dot{}}{m}}_{g1}$ 、补充液氦 ${\stackrel{\dot{}}{m}}_l$ 、超流氦蒸发形成的氦气 ${\stackrel{\dot{}}{m}}_{g2}$ 、通过压缩机抽出的氦气 ${\stackrel{\dot{}}{m}}_{g3}$ 、氦池外部漏热引起的热负载 $Q_l$ 以及氦池内浸泡超导腔带来的热负载 $Q_0$ 。

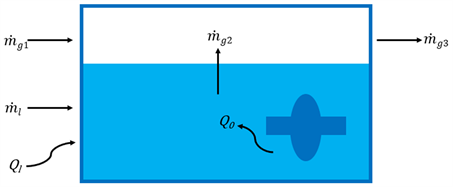
Figure 2. Thermal process diagram of superfluid helium pool operation

图2. 超流氦池工作热力过程图

对于上述的控制系统，通过能量守恒进行热力计算得到下式：

$Q_c+Q_{sl}+Q_{sg}+Q_{liq}+Q_{gas}=Q_e$ (1)

式中， $Q_c$ 为以常量计算的热负载，包括外部漏热导致的热负载 $Q_l$ 及超导腔散热的热负载 $Q_0$ 。 $Q_{sl}$ 和 $Q_{sg}$ 分别为补充液氦和补充氦气引起的热负载。 $Q_{liq}$ 和 $Q_{gas}$ 为氦池内的超流氦和氦气温度变化产生的热负载。 $Q_e$ 为超流氦蒸发吸收的热量。

其中， $Q_{sl}$ 和 $Q_{sg}$ 的热负载为将补气和补液降低到氦池温度产生的热量，以二者的焓差计算，分别如下式所示：

$Q_{sl}={\stackrel{\dot{}}{m}}_l·\left(h_{sl}-h_l\right)\cdot dt$ (2)

$Q_{sg}={\stackrel{\dot{}}{m}}_{g1}\cdot \left(h_{sg}-h_g\right)\cdot dt$ (3)

式中， $h_{sl}$ 、 $h_l$ 、 $h_{sg}$ 、 $h_g$ 分别为补充液氦、氦池内超流氦、补充氦气、氦池上方氦气的焓值。

$Q_{liq}$ 和 $Q_{gas}$ 为储存容器内超流氦和氦气的降温热负载，以二者的比热容 $c_l$ 及 $c_g$ 计算，分别如下式所示：

$Q_{liq}=M_{tl}\cdot c_l\cdot dT$ (4)

$Q_{gas}=M_{tg}\cdot c_g\cdot dT$ (5)

式中， $M_{tl}$ 和 $M_{tg}$ 分别表示容器内超流氦和氦气的质量。

$Q_e$ 为超流氦蒸发吸收热量，其大小由超流氦的汽化潜热 $r_T$ 决定，如下式所示：

$Q_e=r_T\cdot {\stackrel{\dot{}}{m}}_{g2}\cdot dt$ (6)

式中， ${\stackrel{\dot{}}{m}}_{g2}$ 表示单位时间内蒸发的超流氦质量，其大小取决于气液交界面相变的情况。由于超流氦的独特物理性质，其在抽气降压过程中由于气化核心的缺失，液体内部基本不产生气体，因此在降温过程中不会发生和常规流体相同的剧烈沸腾，而是更接近蒸发的状态。在此前提下，由于容器内的超流氦和氦气都为饱和状态，因此超流氦的蒸发量取决于压缩机的抽气量V、补充氦气的质量流量 ${\stackrel{\dot{}}{m}}_{g1}$ 、容器内气腔容积的变化量 $d{V}_g$ ，以及在该状态下的氦气比容 $v_{gT}$ ，如下式所示：

${\stackrel{\dot{}}{m}}_{g2}=\frac{\left(V-{\stackrel{\dot{}}{m}}_{g1}·v_{gT}\right)\cdot dt+d{V}_g}{v_{gT}}$ (7)

3. 氦池降温系统仿真计算

3.1. 仿真理论公式

由传热理论计算可知，在计算超流氦的降温过程中的热力变化时低温氦的各物性参数与温度之间存在复杂的关系，为简化计算过程采用数值解法，以时间步长 $\Delta t$ 对式(1)进行离散化，得到：

$\left[Q_c+{\stackrel{\dot{}}{m}}_{li}\cdot \left(h_{sli}-h_{li}\right)+{\stackrel{\dot{}}{m}}_{g1i}\cdot \left(h_{sgi}-h_{gi}\right)\right]\cdot \Delta t+\left({M^{\prime }}_{li}\cdot c_{li}+{M^{\prime }}_{gi}\cdot c_{gi}\right)\cdot \left(T_i-T_{i+1}\right)=ri·{\stackrel{\dot{}}{m}}_{g2i}\cdot \Delta t$ (8)

$M_{li+1}=M_{li}+{\stackrel{\dot{}}{m}}_{li}\cdot \Delta t-{\stackrel{\dot{}}{m}}_{g2i}\cdot \Delta t$ (9)

$M_{gi+1}=V_c-M_{li+1}\cdot v_{li+1}$ (10)

式中，为方便计算将外部漏热与氦池内部超导腔散热均视作常量，合计为 $Q_c$ 。 $V_c$ 表示超流氦容器内的总容积。而补充液氦与补充氦气的热负载以4.2 K冷箱中的液氦与氦气进入氦池时和氦池内部液氦与氦气在i时刻的焓差计算，因此在计算氦池内超流氦和氦气从i时刻变化到i + 1时刻的热负载时，需要在氦池内原本超流氦质量和氦气质量的基础上增加补液和补气的质量：

${M^{\prime }}_{li}=M_{li}+{\stackrel{\dot{}}{m}}_{li}\cdot \Delta t$ (11)

${M^{\prime }}_{gi}=M_{gi}+{\stackrel{\dot{}}{m}}_{g1i}·\Delta t$ (12)

超流氦的蒸发质量 ${\stackrel{\dot{}}{m}}_{g2i}$ 按下式计算：

${\stackrel{\dot{}}{m}}_{g2i}=\frac{\left(0.001\cdot V_i-{\stackrel{\dot{}}{m}}_{g1i}\cdot v_i\right)\cdot \Delta t+\Delta V_g}{v_i}$ (13)

式中， $V_i$ 表示压缩机的吸气体积流量，由于其单位一般为L/s，故需要使用系数进行单位的转换。 $\Delta V_g$ 表示氦池容器内气腔容积的变化量。

3.2. 仿真参数设置

为显示压缩机减压抽气制冷中氦池的压力波动情况，按照小容积超流氦池设计仿真参数。系统时间步长 $\Delta t$ 设为0.001 s，容器内总容积 $V_c$ 为0.07 m³， $Q_c$ 为20 W。容器内初始液氦质量为5 kg，压缩机的初始抽速为1 L/s。

补充液氦和补充氦气的质量流量均为PID控制，当容器内为稳定状态时液氦的液位高度不变，因此补充液氦和补充氦气的质量流量的调节目标分别为容器内的液体体积和气体体积，调节间隔为0.1 s。补充液氦和补充氦气的状态分别为4.2 K的饱和液氦和饱和氦气，为贴近实际情况，补充液氦与补充氦气的温度和质量流量均设有扰动，温度波动的范围为±0.1 K，流量则设有−0.7~1.3的扰动系数。

抽气的体积流量与压缩机的转速相关，考虑到实际对压缩机的转速进行调节时其转速改变并不是突变的，因此为还原压缩机的实际工作状态，设计压缩机的抽气体积流量在两次调节的间隔当中由原本的抽气量匀速变化到调节的目标抽气量，并且考虑到压缩机转速调节的能力是有限制的，因此两次调节之间的抽气体积流量差最大不超过3 L/s，调节间隔同样设为0.1 s。

仿真过程中，由初始状态开始通过式(8)计算得到时间间隔 $\Delta t$ 后的氦池温度，随后以该氦池温度得到该时刻氦池内其他物性参数，再以该状态为起始继续推算间隔 $\Delta t$ 后的氦池状态。重复迭代最后得到完整的氦池状态参数曲线。

3.3. 吸气量调节控制方程

当前较为普遍的压力波动控制中对压缩机转速的调节仍是通过PID的调节方式，该方法仅仅从压力的角度调节了抽气的体积流量，而实际上最理想的气体抽吸量不仅与当前氦池内的压力有关，也和超流氦的当前物性、气腔容积、补气补液的流量和温度以及当前的热负载密切相关，如果要进一步提高压力波动的稳定性必须结合这些信息对压缩机的抽气量进行精准的调节。为实现该效果则需要对下一次调节间隔内的氦池热力变化进行预计算，得到理想吸气量。以两次调节的时间间隔 $\Delta t^{\prime }$ 对冷量需求 ${Q^{\prime }}_e$ 的估算为：

$\begin{array}{c}{Q^{\prime }}_e=\left[Q_c+{\stackrel{\dot{}}{m}}_{li}\cdot \left(h_{sli}-h_{lt}\right)+{\stackrel{\dot{}}{m}}_{g1i}\cdot \left(h_{sgi}-h_{gt}\right)\right]\cdot \Delta t^{\prime }\\ +\left(M_{li}-\frac{{\stackrel{\dot{}}{m}}_{g2i}·△t^{\prime }}{2}\right)\cdot \left(h_{li}-h_{lt}\right)+\left(M_{gi}+\frac{{\stackrel{\dot{}}{m}}_{g2i}\cdot \Delta t^{\prime }}{2}-\frac{0.001\cdot V_i\cdot \Delta t^{\prime }}{2\cdot v_{gi}}\right)\cdot \left(h_{gi}-h_{gt}\right)\end{array}$ (14)

式中， $h_{lt}$ 和 $h_{gt}$ 分别表示目标温度(2 K)下的超流氦及气氦焓值，在计算氦池内超流氦和氦气的热负载时由于前后物性变化较大，不能再用比热容计算，改用焓差进行求解。

求得冷量需求 ${Q^{\prime }}_e$ 后代入下式即可得到理想吸气量 $V^{\prime }$ ：

$V^{\prime }=1000\cdot v_{gi}\cdot \left(\frac{{Q^{\prime }}_e}{r_i\cdot \Delta t^{\prime }}+{\stackrel{\dot{}}{m}}_{g1i}\right)$ (15)

在仿真过程中，以理想吸气量 $V^{\prime }$ 代替原本通过PID控制的吸气量V即可得到以精确控制方法运行的氦池模拟结果。

4. 仿真结果及分析

利用MATLAB按照上述控制方程进行仿真模拟，其中低温氦的物性参数采用HEPAK软件查询得到。HEPAK是一个通过基本状态方程计算氦热物理量的计算机程序。状态方程从0.8 K至1500 K的温度范围内有效，包括超流体区域、λ线和液–汽两相区域；HEPAK的这些方程可以在1000 bar以内的压力范围适用。

分别使用PID控制和精确调节控制压缩机的抽气量，其稳定状态下的压力波动对比如图3所示。在相同外界条件、相同调节间隔、相同抽速调节能力的情况下，相比于使用PID对压缩机抽气量进行调节，使用精确调节控制后氦池内的压力波动稳定性得到了显著提高，压力波动偏离2 K饱和氦蒸气压3129.26 Pa的范围由±0.25 Pa提高至±0.15 Pa。在压力偏离预定值时，精确调节的反应也相比PID调节更迅速，有效提高通过吸气量压制扰动的能力。使用均方根误差RMSE计算两种不同调节方法下压力偏离真值的离散程度，误差由PID调节的6.53 × 10⁻⁵降低到精确调节的3.45 × 10⁻⁶。

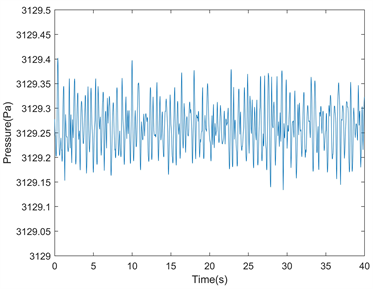
(a) PID调节 (b) 精确调节

Figure 3. Comparison of simulated pressure fluctuations

图3. 仿真压力波动对比图

抽气量波动对比如图4所示，使用PID调节和精确调节的抽气量 也有明显的区别。尽管提高了压力波动的稳定性，精确调节的抽气量变化幅度相较于PID调节有明显的提高，这是由于精确控制对于状态的偏差会形成即时的响应调节，而PID控制由比例调节、积分调节、微分调节共同作用，在调节时精确控制更倾向于快速压制压力偏差，因此调节的抽气量波动范围会更大。所以使用精确调节也会在一定程度上对压缩机的调节能力提出要求。

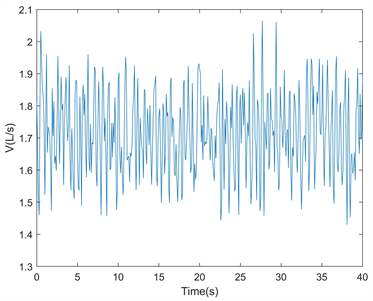
(a) PID调节 (b) 精确调节

Figure 4. Comparison of simulated pumping volume fluctuations

图4. 仿真抽气量波动对比图

5. 结论

采用MATLAB软件，对小型超流氦减压制冷低温系统进行了热分析，在此基础上完成了系统的热仿真模拟。主要结论如下：

1) 建立一超流氦池抽气减压降温过程的模型，该模型能够反应降温过程中超流氦池内部各物性参数状态；

2) 提出一种结合氦低温物性及氦池状态的压缩机抽气量精确控制方法，其目的在于提高抽气减压制冷过程中超流氦池的压力波动稳定性；

3) 对比普遍采用的PID调节方法与精确控制方法在仿真模拟中的表现，在相同条件下采用精确调节的方法将压力波动范围由±0.25 Pa提高至±0.15 Pa，均方根误差由6.53 × 10⁻⁵降低到3.45 × 10⁻⁶，证明该控制方法可行性。