1. 引言
经编行业发展了240余年,得益于精密机械的制造技术和经编材料的品质升级,经编机行业迎来了快速发展 [1] ,同时数字化时代的影响,也将经编机从原本的传统机械式结构向着电子化改造。对于织物数量的追求,通过加快主轴转速和横移的节奏,在单位时间内获取更多的织物,矛盾也在此处——梳栉结构作为经编机中的高速往复运动装置,不断高速化也让梳栉横移运动加速,实际运作中就更容易产生撞针、擦针、振动等现象 [2] ,这给横移机构的设计增添了不少难度。
经编机转速的提高,主轴旋转一周的时间就会缩短,留给梳栉运动的时间就越少,因此电子横移部分的移动精度变得至关重要,不仅直接决定织物质量,其性能高低也决定着经编机转速的快慢 [3] 。梳栉本身内部存在的静态和动态特性,也影响着导纱运动的平稳性 [4] 。国内学者张琦、夏风林等,对梳栉部分的横移、摆动进行了加速度与位移测试,并提出了解调、轻质和阻尼三种减振方法。国内外生产的经编机一般采用的是金属弹簧或橡胶减振器 [5] ,本文将对梳栉横移部分进行动力学特性分析,并借助ANSYS软件进行振动仿真测试,在此基础上寻找减振措施。
2. 梳栉动力学特性
2.1. 动力学模型
在经编机运行当中,梳栉分横移和摆动两个运动,由两个运动结合构成一个循环 [6] 。本节根据电子横移机构与梳栉的连接,考虑只横移不摆动的梳栉运动状态,建立横移方向动力学模型,图1为梳栉部分结构示意图。
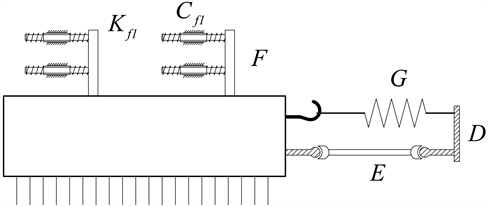
Figure 1. Schematic diagram of comb motion mechanism
图1. 梳栉运动机构示意图
梳栉横移运动由电子横移装置带动,针床通过梳栉回复组件G、顶杆E连接金属块D,从而实现与电子横移装置的连接固定,梳栉吊架F通过滚珠套安装在导轨上与梳栉主臂连接,并在导轨两端安装弹簧,实现快速复位。为了在仿真中运用数学工具对其振动特性进行分析计算,将梳栉吊架及导轨弹簧部分简化为弹簧阻尼系统,将主要构件例如顶杆、针床等视为刚性体研究,只考虑针床平面左右横移运动,外界力只受到电机带来的激励 [7] [8] 。
横移系统由伺服电机提供驱动力,通过滚珠丝杆将电机轴传递来的转矩转化为线性运动,带动针床横移垫纱运动。设最初电机提供的力为F(t),顶杆E处受到F(t)的推拉力,带动针床运动,梳栉吊架在导轨中受到弹簧限制,每把梳栉与导轨弹簧产生阻尼Cf1,对应弹簧的刚度系数为Kf1,将吊架、顶杆、导轨、针床等结构看做一个独立的振动系统,梳栉的针床与导纱针针块看做一体,设质量为m,建立一个单自由度的动力学模型,如图2,该系统作往复横移运动,受到电机周期激励,属于强迫振动体。x(t)为梳栉部分受力后沿针床方向的位移;k为导轨上弹簧的等效刚度系数,N/mm;F(t)为横移动力装置施加在系统上的作用力,N;m为梳栉针床整体的质量;c为导轨和吊架的等效阻尼系数。
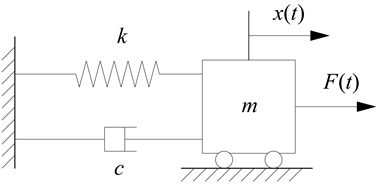
Figure 2. Single degree of freedom dynamics model of comb transverse mechanism
图2. 梳栉横移机构单自由度动力学模型
2.2. 动力学方程
在任意激励或作用时间极短的脉冲激励下,单自由度系统的响应通常没有稳态响应,只有瞬态响应,这种情况下的系统响应可通过拉普拉斯变换法进行求解。
根据图2所示系统,F(t)为受电机的任意激励,则系统的运动微分方程为:
(1)
设系统的初始位移和速度分别为:
则对方程(1)两边分别取拉普拉斯变换得:
(2)
由方程(2)解得:
(3)
对式(3)取拉普拉斯反变换,若系统初始位移和速度均为零,可简化为:
(4)
式(4)就是著名的杜哈梅积分,表示为系统对零初始条件的响应。在横移运动过程中,伺服电机提供给横移动力装置的驱动力的频率跟梳栉横移系统频率的比值对梳栉横移运动的响应有比较大的影响,驱动力频率大小可通过调节经编机速度来改变,下文对横移运动进行进一步分析。
3. 梳栉振动分析
3.1. 振动原因
根据所设计织物的不同花型纹路,梳栉横移进行机械的往复运动,属于“静止→动作”的启停运动模式,并且梳栉处于一个高速运动环境下,经编机在编织新的横列时,梳栉所受的横移驱动力的方向都会发生反向,同时梳栉横移运动的方向也会滞后跟随反向 [9] ,梳栉不断受到受迫振动,其频率随转速上升而上升,不断受到激振作用,处于高频受迫振动的经编梳栉 [10] ,将会影响横移的定位精度,产生撞针、擦针等危险现象。
3.2. 减振方法
根据动力学振动理论分析,减振分为三种方法:阻尼、隔振、吸振技术。在梳栉横移中,根据其运动及结构特点,可尝试以下方式来进行减振。
(1) 避开共振区间
梳栉做自由振动时不受外力干预,振动的频率仅与系统的固有特性有关,当梳栉的固有频率接近横移动力装置的振动频率,且激励自由度与振型相匹配时,会产生共振现象,需要进行机械的振动试验和动态分析,来避开共振区间。改变梳栉针床的材料,增大或是减小质量,其固有频率会随之减小或增大;刚度增大,结构的固有频率增大,但是刚度继续增大,固有频率不会无限增大。
(2) 积极隔振
伺服电机作为激励源,需要在短时间内进行高速正反转,带来多余振动。运用积极隔振技术,将电子横移安装座的外框进行加厚加固,使电机这一振源向四周的振动传递减少 [11] 。滚珠丝杆的导程对电机的加速度也有影响,影响梳栉横移的精度包括滚珠丝杆的精度、伺服电机与滚珠丝杆的传动精度和滚珠丝杆定位端轴承的轴向定位精度 [12] 。在本机型中,滚珠丝杆导程选用为28~32 mm。
(3) 阻尼减振
梳栉吊架连接导轨和针床,通过滚珠套在导轨上进行横移运动,同时滚珠套两端装有复位弹簧,使梳栉在横移之后能进行快速的复位,同时减小“静止–运动”间隙中的颤振。根据式5求得弹簧刚度K = 233 N/m。
(5)
其中K——弹簧刚度,N/m;
G——弹簧材料切变模量,弹簧材料为65 Mn,取
;
D——弹簧线径,m;
d2——弹簧中径,m;
n——弹簧有效圈数。
(4) 优化驱动力输入规律
随着经编机主轴转速提高,凸轮跟推杆的接触碰撞愈发剧烈,伺服电机驱动的电子横移系统逐渐代替凸轮,控制横移运动 [13] 。根据驱动力输入方式的不同,梳栉横移到的位置也不同,可以通过等速、正弦加速度、余弦加速度、五次多项式等运动规律作为驱动力的输入规律,根据理论来讲,等速运动规律因在启停阶段有速度突变,会产生强烈的刚性冲击,只适用于低速。等加速、等减速和余弦加速度也有加速度突变,会引起柔性冲击,只适用于中、低速。正弦加速度运动规律的加速度曲线是连续的,没有任何冲击,可用于高速。
3.3. 振动仿真
3.3.1. 固有频率
仿真测试采用KS系列高速经编机模型,已投入实际生产使用,最高转速可达到3000 r/min。将横移结构导入ansys workbench模块进行模态分析,得到梳栉部分各阶固有频率,根据振型和激励自由度,可以推算出横移结构中的共振点。表1为梳栉前8阶的固有频率仿真测试结果,图3为振型。

Table 1. First 8 natural frequencies of comb
表1. 梳栉前8阶固有频率
因第4阶振型主要表现为z方向的平移,这与激励频率方向相同,该振型下固有频率24 Hz对应经编机的转速为1450 r/min,由于共振带的存在,当外界激励频率接近固有频率时,系统也会发生共振,在行业中一般取15%~20%的范围作为共振带,横移机构第4阶模态为24 Hz左右,15%的频率范围对应 ± 3.6 Hz,共振带为20.4~27.6 Hz,给定激励频率需要避开这一范围,防止发生共振。
3.3.2. 驱动力输入规律
伺服电机驱动力按照四种形式输入,分别按正弦、正弦加速度、余弦加速度、五次多项式运动规律作为驱动力的输入方式,得到的位移曲线与理想位移曲线作对比,来得到位移偏差,选择理想的驱动力输入方式。设定经编机转速为2300 r/min时的横移状态,整个横移周期为26.08 ms,分两次横移两次摆动,针前横移时间为3.99 ms,针背横移时间为12.30 ms,为方便观察,取两针位移1.8 mm作为横移的距离。横移所用伺服电机功率为1500 W,根据其额定转矩算得轴向驱动力峰值为593.5 N,算上纱线等阻力后取为600 N,其中取阻尼系数200 N·s/m。设定导纱针横移方向为正方向,跟踪导纱针头的运动路径。其仿真模型如图4。

Figure 4. Simulation model of comb part
图4. 梳栉部分仿真模型
正弦规律输入函数为:
(6)
正弦加速度规律为:
(7)
余弦加速度规律为:
(8)
五次多项式规律为:
(9)
其中F0 = 600 N,t总分别取针前针背的横移时间,t为当前横移所用时间,F为持续变化的驱动力。
所得位移曲线如图5所示:
 (a)
(a)  (b)
(b) 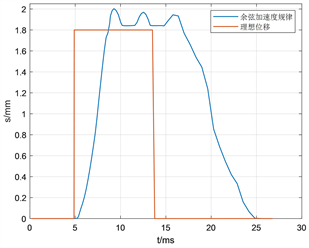 (c)
(c)  (d)
(d)
Figure 5. Displacement curves with different input rules (a) Sine law (b) Law of sinusoidal acceleration; (c) Law of cosine acceleration; (d) Law of quintic polynomials
图5. 不同输入规律的位移曲线(a) 正弦规律;(b) 正弦加速度规律;(c) 余弦加速度规律;(d) 五次多项式规律
由图5可知,相同条件下,不同驱动力输入规律的运动路径不同,理想状态下,8.88~13.77 ms处于摆动状态,梳栉在横移方向上应尽量保持不动或在安全范围内波动,安全范围指导纱针穿过槽针时的空隙,针间距减针宽为0.38 mm,正弦规律跟五次多项式规律在此时间段波动较大,部分时间位移偏差接近或超过0.38 mm,若驱动力按此规律输入,容易在摆动(垫纱)过程中造成撞针现象,导致故障发生。正弦、余弦加速度输入规律在此时间段位移偏差较小,符合横移运动规律,但在某些时间段,余弦加速度规律会有由加速度突变带来的柔性冲击,影响位移变化,正弦加速度的位移曲线较其他三种更为平滑,误差较小,适合作为驱动力的输入规律。
4. 结论
1) 通过对梳栉横移结构与运动的动力学分析研究,建立了经编机梳栉横移的动力学模型,这是一种单自由度受迫振动模型,通常只有瞬态响应。同时使用Ansys workbench对梳栉受力运动状态进行瞬态分析,得到不同仿真结果,提出了避振隔振和阻尼等减振措施。
2) 高速经编机的工作频率在6.7~50 Hz,梳栉部分在振型与激励自由度匹配时的固有频率在24 Hz左右,位于工作时给定的激励频率内,故经编机在正常工作时,生产速度应该避开24 Hz这一共振区间,这样可有效降低机体的机械振动,提高横移时的定位精度,让经编机工作时能有更好的稳定性。
3) 在高速情况下,正弦加速度规律作为伺服电机的驱动力输入规律最为平稳,可以在经编机横移部分运行过程中达到较为精确平稳的目的。