1. 引言
目前,相关滤波(Correlation Filter)原理被广泛地应用于信号处理、图像检测与视频跟踪等领域。基于相关滤波器实现目标跟踪的基本思想是对输入图像进行训练并得到一个滤波模板(也即滤波器),利用该滤波模板对下一帧输入图像进行响应输出,最大响应值所对应的位置就是目标的预测位置。
2010年,Bolme等人 [1] 构造了一种最小均方误差和输出的相关滤波器并将其首次应用于目标跟踪。在此基础之上,很多学者对该算法的改进相继出现,跟踪的效果越来越好。CSK [2] 算法在MOSSE的基础上引入了循环矩阵和核的概念。KCF [3] 与CN [4] 算法在此基础上对多通道特征分别进行改进。KCF比DCF跟踪效果略好,但速度比线性核要慢很多。2021年,Safaei [5] 和Zhong [6] 将分块采样方法引入相关滤波目标跟踪算法中,提出自适应像素级分块的跟踪算法。Zhang等 [7] 提出一种基于块–核相关滤波的目标跟踪算法。
基于相关滤波器的跟踪方法最大的优势是速度快,速度快的原因在于利用快速傅里叶变换 [8] 来代替卷积计算。STC [9] 方法提出一种新的相关滤波跟踪框架,在该框架中引入了时空上下文信息。但由于STC的尺度更新策略仅依赖于响应输出的最大值,对一些跟踪场合,跟踪效果并不鲁棒。为更好地解决尺度更新问题,文献 [10] 和 [11] 分别提出了DSST与SAMF跟踪算法并提出了各自的尺度更新方案。文献 [12] 在KCF的基础上为减轻其循环移位时的边界效应问题提出了SRDCF算法,但该算法运行速度很慢,无法达到实时性。
以上基于相关滤波的跟踪算法,虽然跟踪效果越来越好,但速度却越来越慢,本文提出了以Radon变换数据作为特征对目标进行外观建模的一种新的相关滤波目标跟踪算法,能够实现快速且鲁棒的跟踪效果。该算法通过训练目标图像的Radon变换数据作为相关滤波模板。
2. 基于Radon变换数据外观建模的相关滤波目标跟踪算法
2.1. 基于Radon变换数据的滤波训练
考虑一个跟踪场景,第k帧时,可以将跟踪目标及周围一定区域的图像进行Radon变换(如图1所示),到k + 1帧时,可在同样位置的区域进行Radon变换,如果相邻两帧目标状态变化很小而视为近似一致,那么相邻两帧的Radon变换的结果也非常相近。显然,k + 1帧目标的中心在k帧图像中或保持不变或仅发生微小的偏移。
 (a) frame k
(a) frame k  (b) frame k + 1
(b) frame k + 1
Figure 1. The Radon transformation of the target area
图1. 对目标区域进行Radon变换
首先,对Radon变换区域进行权重加窗处理,从而有:
(1)
其中,
称为二维卷积符号,
,
表示Radon变换区域,
为对Radon变换区域训练的滤波模板,
称为Radon变换区域的响应输出或置信图,本文称为置信图。
表示Radon变换区域的单通道像素值,
为Radon变换区域各像素的加窗函数,其定义为:
(2)
其中,H表示汉明窗矩阵,a是汉明窗矩阵归一化系数,
表示尺度参数,取值为目标宽度和高度之和的一半,因此每一帧都需要更新。
为描述方便,令
,代入式(1)有:
(3)
对式(3)两边进行Radon变换,并根据Radon变换的性质有:
(4)
其中,
表示一维卷积运算符号。
、
与
均是矩阵,将其分别表示为
、
、
,代入式(4)可得:
(5)
其中,m表示从m个角度进行Radon变换投影。
对式(5)两边矩阵的每一列进行一维傅里叶变换,由卷积定理最终可得:
(6)
其中,
表示矩阵对应元素相除。
由式(9)得到相关滤波训练模板的闭合解为:
(7)
在实际计算时,无需具体求出
,式(14)左边的
可作为整体参与运算,因此可将其视为实际的滤波模板。
2.2. 置信图
本文提出的相关滤波框架的置信图定义如下:
(8)
其中,b是归一化系数,x*与y*表示目标中心位置。
与
分别表示尺度参数与形状参数。
在相邻两帧的Radon变换区域,目标发生了位移时,置信图的最大值点也将发生偏移,由此可以反求Radon的旋转中心,即目标在下一帧的位置。

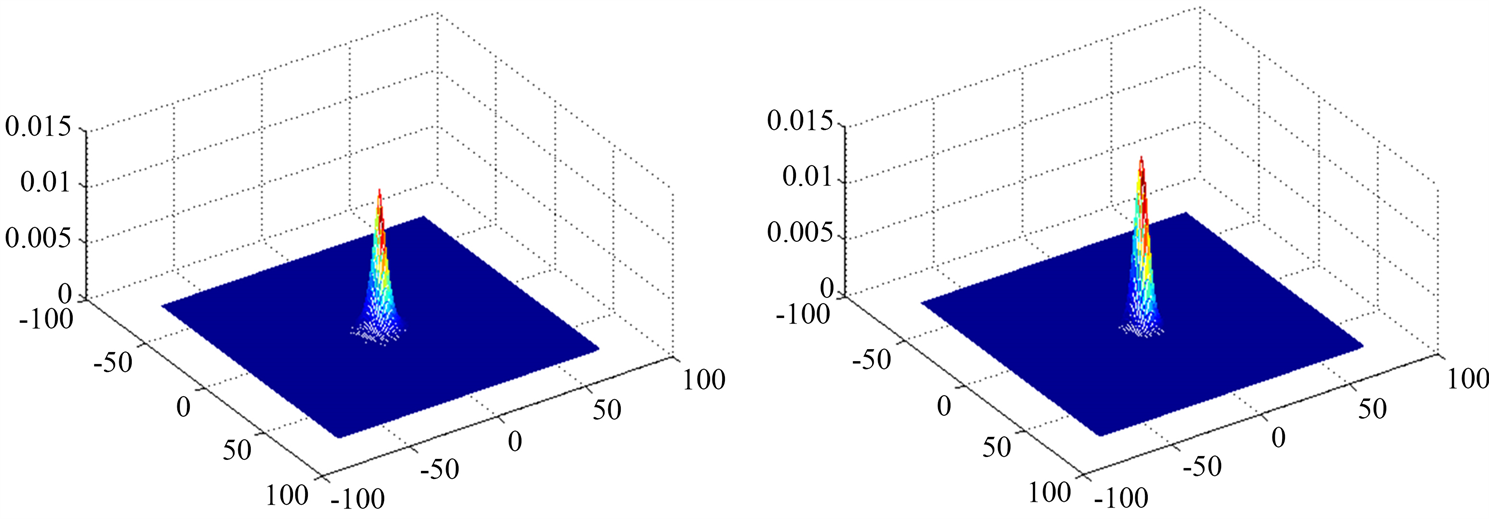
(a)
, max = 0.0019 (b)
, max = 0.0079(c)
, max = 0.0124 (d)
, max = 0.0149
Figure 2. Four confidence maps with different shape parameters in 3D
图2. 四个不同形状参数置信图的三维示意图
如图2所示为大小为150*150的四个不同形状参数置信图的三维示意图,z坐标表示置信值,形状参数分别为0.6,1,1.4,18,尺度参数均为4.5。示意图的顶部对应置信图的中心区域,而底座部分对应置信图中心外围非趋近于0的部分(底部大部分均趋近于0)。为叙述方便,称底座非趋近于0的区域为底座的有效区域。
2.3. 目标定位
我们假设目标的状态在第一帧时已经初始化,在k帧时,我们要计算出当前帧置信图的滤波模板
,用其计算更新下一帧所使用的训练模板
并进行下一帧的目标检测。
将更新后的滤波模板代入式
,可得:
(9)
经Radon逆变换可得到k + 1帧的置信图,
(10)
进一步,便可求出目标在k + 1帧的置信图的相对位置:
(11)
滤波模板的更新采用历史累积方式:
(12)
为保持
在两帧之间的稳定性,变化参数
一般取一个较小的值。经多次实验,本文取该参数值为0.075。
2.4. 尺度更新
相关滤波框架本身不具备尺度更新的方式,本文受STC算法中尺度更新方法的启发,提出一种新的尺度更新方式,考虑到相邻两帧置信图对应位置之间值的比值与相邻两帧目标尺度的比值近似于成正比关系,若只以
中某一个值计算尺度的变化,难以得到鲁棒且精确的结果,本文采用了置信图中所有像素置信值求和的方法,具体方法如下:
(13)
从而,
(14)
但为了使尺度更新的结果更加鲁棒以及避免出现尺度变化过大或过小的情况,依然采用加权的方式,即:
(15)
(16)
式中
称为权重参数,本文取值为0.8。
表示取前n帧的尺度平均值,本文取n = 5。同时更新尺度参数,即:
(17)
3. 跟踪算法流程
本文提出基于Radon变换数据外观建模的相关滤波目标跟踪算法,其具体流程如下所示:
4. 实验结果与分析
4.1. 实验配置
为验证本文算法的有效性,本节对15组公开具有各种挑战性的视频图像序列进行了测试,并与当前5种优秀的基于相关滤波的目标跟踪算法以及其他4种优秀算法进行对比。这5种相关滤波算法包括:CN [4] 、DSST [10] 、KCF [3] 、SRDCF [12] 和STC [9] 算法。另四种优秀算法包括:ASLA、L1APG、SCM和Struck。本文实验所用的视频图像序列及其描述如表1所示,测试视频序列均来自TB-50和TB-100公开数据集。

Table 1. Video image sequence used in this chapter
表1. 本章实验所用的视频图像序列
为叙述方便,本文提出的基于Radon变换数据外观建模的相关滤波目标跟踪算法简称为RBT (Radon-based object tracking),并在Matlab平台下实现了该算法。本文实验均在Matlab平台下运行。
本文算法参数设置为:式(7)中的Radon变换的投影间隔gap设为20,投影范围设置0˚~179˚。
实验均在Intel i5-3230 2.60GHz的CPU、4G内存的PC机上完成。
4.2. 实验结果及分析
本节从跟踪精度与实时性两个方面来评价提出的跟踪算法。跟踪精度使用中心定位误差(CLE)和跟踪窗重叠率(OR)。其中,中心定位误差的阈值设为20像素,成功率阈值设为0.6。实时性采用每秒处理的帧数来衡量。
表2与表3列出了10种算法在15个图像序列上的平均中心点误差、平均运行帧率和平均重叠率。其中,红色加粗表示最好的结果、蓝色加粗表示次好的结果、橙色加粗表示第三较好的结果。本文提出的RBT算法在平均中心定位误差和平均重叠率上都好于其他对比算法。
表2最后一行展示了各算法的运行帧率,结果表明本文算法的平均运行帧率达73.2帧,仅低于STC算法。
图3显示了10种算法在所有测试视频序列上的精确度曲线和成功率曲线,同样说明了本文算法的有较好的鲁棒性及实时性。

Table 2. Mean center locating error (in pixel)
表2. 平均中心定位误差(像素)

Figure 3. Precision plots and success-rate plots for all image sequences with different algorithms
图3. 不同算法在所有图像序列上的准确度曲线与成功率曲线
5. 总结
本文提出了一种新的相关滤波跟踪算法,在该算法中对目标区域图像原始像素进行Radon变换,以Radon变换的投影数据为特征表示并进行滤波训练,并提出一种新的尺度更新方法,能较好地适应目标尺度的变化。
此外,本文所提出的跟踪算法也可以视为一种框架,因为投影的对象不仅仅可以是原始像素的灰度,还可以是多通道颜色值、HOG等其它属性。同时,本章提出的基于Radon变换数据的外观建模同样适用于其它跟踪框架,这些均可做进一步的研究。
基金项目
湖南省教育厅优秀青年项目(19B301)。