基于COMSOL MULTIPHYSICS的多层介质悬臂结构特性研究

The Multi-Media Cantilever Structure Characteristics Research Based on COMSOL MULTIPHYSICS

摘要: 本文对多层介质悬臂梁结构特性进行了研究。根据Castigliano位移理论，对等效单层介质模型的结构刚度进行了修正，推导出适合于多层介质的等效结构刚度通式，更准确地表征出多介质悬臂梁结构的力电特性。同时，利用COMSOL Multiphysics软件对多介质层悬臂梁结构进行模拟分析，结果表明，当介质层数从2层增加10层时，等效结构刚度增加了1.9671 N/m，系统基本频率提高了22 Hz。在偏置电压为8 V的条件下，随着悬臂梁内部层数从2层增加到10层时，位移量从613 nm减小到544.2 nm。分析得出，同一悬臂梁随着内部介质层数的增加，由于各层材料的杨氏模量和热膨胀系数不同，层与层之间的形变产生了相互抑制作用，同时各介质层之间存在的静摩擦力产生了粘滞效应，等效结构刚度逐渐增大；固有频率及动态性能随着介质层数的增加而提高。

Abstract: Characteristics of multi-media cantilever structure is studied in this letter. According to Castigliano displacement theory, stiffness formula of single-medium model is revived, an general formula which can accurately represent the electrical characteristics of multimedia structure is deduced. Cantilever structure is simulated with the use of COMSOL Multiphysics. It turns out that the equivalent stiff-ness increases by 1.9671 N/m and the fundamental frequency increased 22 Hz when the layer raise form 2 to 10. In the same load, the deformation decreased from 613 nm to 544.2 nm. With the increasing of layers, deformation between the layers generates inhibition because of different Young’s modulus and thermal expansion coefficient. Meanwhile, static friction of layers brings out viscous effect and enhances the equivalent stiffness. Natural frequency and dynamic property of the system improved with the increasing of medium layers.

1. 引言

随着计算机技术和力学理论的发展，有限元方法在微机械结构的设计和分析中应用发挥了重要作用 [1] 。例如，以复合材料层合结构悬臂梁为研究对象，推导层合结构悬臂梁振动特性公式，计算层合梁的低阶固有频率，对复合材料层合结构悬臂梁的振动特性开展研究 [2] 。采用等效刚度柱法对具有“跨变”的单层铰接排架建立方程求解 [3] 。在实际应用中，由于光学特性和机械特性的要求，微机械结构部分往往为多介质结构，目前对多介质层微机械结构的研究多针对于两层和三层介质的微机械特性研究，或做近似单层处理，例如，氧化物/金属 [4] 和Si₃N₄/a-Si:H/Si₃N₄ [5] 结构，而对于由GaAs/Al_0.9Ga_0.1As III-V族材料组成的DBR结构的模拟还没有见报道。本文针对DBR微机械悬臂梁结构，根据Castigliano位移理论，对等效单层介质模型的结构刚度进行了修正，推导出适合于多层介质的等效结构刚度通式，更准确地表征出多介质悬臂结构的力电特性。同时，给出了多介质层模型的载荷-位移关系和应力分布情况，并分析了不同介质层数对系统固有频率和动态性能的影响。

2. 多介质层理论

Figure 1. DBR structure of GaAs/Al_0.9Ga_0.1As

图1. GaAs/Al_0.9Ga_0.1As DBR结构

DBR结构(如图1所示)的机械特性可以通过应力与应变关系进行表征。根据胡克定律，弹性材料应力与应变量之间的关系式为 [6] ：(其中σ表示应力，ε表示应变量，E表示材料的杨氏模量)

$\sigma =\epsilon \ast E$ (1)

根据Castigliano位移理论，推导出多介质层各层之间的应力分布为 [7] ：

$\begin{array}{l}{\sigma }_1=E_{1}b\left(z-z_N\right)\\ {\sigma }_2=E_{2}b\left(z-z_N\right)\\ ⋮\\ {\sigma }_N=E_{N}b\left(z-z_N\right)\end{array}\}$ (2)

其中 $z_N={\displaystyle \underset{I}{\sum }\left(z_i{E}_I{A}_I\right)}/{\displaystyle \underset{i}{\sum }\left(E_i{A}_I\right)}$ ，b ( $\epsilon =a+bz$ )为表征应变与坐标轴之间的参数。从公式(2)可知多介质层各层的应力分布与各层材料的弹性模量和几何位置是密切相关的。将多介质层结构等效成单层介质模型，等效材料属性的设定必然对计算结果产生很大的影响。

杨氏模量与刚度均为表征材料弹性形变的结构参数。杨氏模量表征物质微观性质，而刚度表征物质宏观的性质，因此对于多层介质定义其等效结构刚度更能从宏观上表征材料特性。

对于单层介质悬臂梁模型，其结构刚度可以表示为 [7] ：(其中E表示材料的杨氏模量，L，w，h分别表示悬臂梁的长、宽、高)

$k=\frac{E{h}^{3}w}{4l^3}$ (3)

多层介质悬臂梁结构的理论模型如图1所示。根据Castigliano位移理论，可以推导出多层介质的等效结构刚度为：

$\begin{array}{c}k=\frac{E_1{S}_1}{l^3}\left[\frac{h_1^2}{4}+z_1\left(z_1-\frac{z_1{E}_1{S}_1+z_2{E}_2{S}_2+z_3{E}_3{S}_3+\cdots +z_n{E}_n{S}_n}{E_1{S}_1+E_2{S}_2+E_3{S}_3+\cdots +E_n{S}_n}\right)\right]\\ +\frac{E_2{S}_2}{l^3}\left[\frac{h_2^2}{4}+z_2\left(z_2-\frac{z_1{E}_1{S}_1+z_2{E}_2{S}_2+z_3{E}_3{S}_3+\cdots +z_n{E}_n{S}_n}{E_1{S}_1+E_2{S}_2+E_3{S}_3+\cdots +E_n{S}_n}\right)\right]\\ +\frac{E_3{S}_3}{l^3}\left[\frac{h_3^2}{4}+z_3\left(z_3-\frac{z_1{E}_1{S}_1+z_2{E}_2{S}_2+z_3{E}_3{S}_3+\cdots +z_n{E}_n{S}_n}{E_1{S}_1+E_2{S}_2+E_3{S}_3+\cdots +E{}_{n}S{}_n}\right)\right]\\ +\cdots +\frac{E_n{S}_n}{l^3}\left[\frac{h_n^2}{4}+z_n\left(z_n-\frac{z_1{E}_1{S}_1+z_2{E}_2{S}_2+z_3{E}_3{S}_3+\cdots +z_n{E}_n{S}_n}{E_1{S}_1+E_2{S}_2+E_3{S}_3+\cdots +E_n{S}_n}\right)\right]\end{array}$ (4)

其中 $E_1,E_2,E_3,\cdots ,E_n$ 为第n层材料的杨氏模量； $S_1,S_2,S_3,\cdots ,S_n$ 表示第n层材料的横截面积；L为悬臂的长度， $h_1,h_2,h_3,\cdots ,h_n$ 为第n层介质层的厚度。 $Z_1,Z_2,Z_3,\cdots ,Z_n$ 为第n层中心轴的位置。从多层介质等效结构刚度的通式可以看出，等效结构刚度中考虑了各层介质的几何位置和杨氏模量，并且对各层介质之间的耦合关系也进行了考虑，与等效的单层模型结构刚度的计算公式相比更能准确表征多层介质结构的机械特性。

金属有机物化学气相沉积法(MOCVD)作为材料的基本生长方法，具有操作简便、生长速度快的优点，但由于以气体为生长源，真空度比较低的原因，MOCVD方法生长的GaAs/Al_0.9Ga_0.1As异质结之间存在的界面扩散，使界面存在较为粗糙且不均匀的缺点 [8] 。根据多层介质等效结构刚度理论公式可以计算出不同介质层数的等效结构刚度。计算结果表明等效结构刚度k随着介质层数的增加而提高，其原因是由于各层材料的弹性模量和热膨胀系数不同，层与层之间的形变产生了相互抑制作用，同时各介质层之间存在的静摩擦力产生了粘滞效应，使得等效结构刚度逐步增加。

3. 实验结果与分析

COMSOL Multiphysics是一款有限元分析软件，对于三维模型的建立选用结构力学–平面应力、静电场、移动网格(ALE)三个应用模块。建立悬臂梁模型后设定不同求解域的材料参数及边界条件，多层介质模型材料参数如表1所示，边界条件的设定如下：悬臂梁模型一端固定，另一端自由运动。悬臂梁底边界通过一个指定的偏压势能V_in连接到一个电压源，腔体底部接地，其他边界为电绝缘。在求解器参数设定中，收敛误差设定为10⁻⁶，为了避免系统不收敛，迭代上限设置50。求解器收敛后，就可以进行后处理，其后处理结果可以进行多种形式的显示。

Table 1. Material parameter settings of GaAs/Al0.9Ga0.1As

表1. GaAs/Al_0.9Ga_0.1As材料参数设置

3.1. 多介质层模型载荷–位移关系分析

为了准确表征多介质悬臂结构的机械特性，本实验分别模拟了2，4，6，8，10层介质在相同偏置电压下的形变效果图，利用软件的边界积分功能，得出最大形变下的静电力F，并根据公式F = k*d，得到不同介质层模型的等效结构刚度。

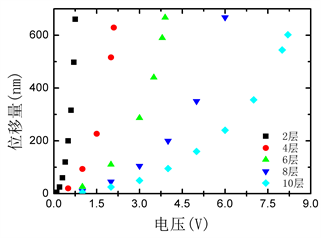
Figure 2. Load displacement relationship of cantilever models with different media layers (each layer has the same thickness)

图2. 不同介质层数(每层厚度相同)悬臂模型载荷–位移关系

图2显示了不同介质层数悬臂梁模型(每层厚度相同)的载荷–位移关系，从模拟结果可以得出，随着介质层数的增加，在相同的负载下位移量逐渐减小，最终使得下拉电压会随着DBR对数的增加而增加，这与文献中的报道相一致 [9] ，但最大位移相同，遵守1/3位移定律。

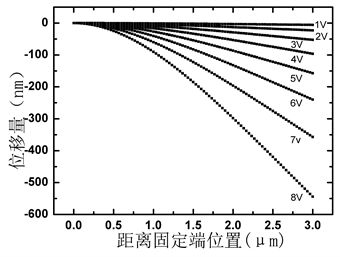
Figure 3. Load displacement relationship diagram of a 10 layer medium mode

图3. 10层介质模型载荷–位移关系图

Figure 4. Stress distribution of a 10 layer medium model, the internal illustration shows the stress distribution in the YZ plane

图4. 10层介质模型应力分布情况，内插图为YZ平面的应力分布情况

图3显示了10层介质模型的载荷–位移关系图，横坐标表示距离固定端的位置，纵坐标表示位移量，8条曲线分别表示在载荷为0 V到8 V，步长为1 V的条件下，悬臂的形变量。从曲线可以看出，在相同步长的载荷条件下，悬臂的形变并不是均匀线形变化的，而是呈现出开始增加比较缓慢，随后形变效果逐渐扩大的特点。图4显示了10层介质模型米塞斯应力分布情况，结果表明，在悬臂模型中固定端应力最大，因此，固定端最容易毁坏，在悬臂设计过程中，可以在上面做一加强筋来增强悬臂的可靠性 [10] 。

3.2. 多介质层模型频率响应分析

研究多介质层悬臂梁模型的固有频率，对考察悬臂梁结构的机械运动及机械性能具有非常重要的作用。设置求解器中分析类型为固有频率，模拟结果可以同时显示在固有频率下弯曲模态和扭转模态。对于两层介质模型的前六阶固有频率分别为：33.2126 KHZ、209.2876 KHZ、599.1183 KHZ、1.2136 MHZ、2.0861 MHZ、3.1013 MHZ，并且随着频率的增加，悬臂呈现6个振动模态，包括两个弯曲模态和三个扭转模态(下图5所示)，在频率3.1013 MHZ下弯曲模态与扭转模态发生交叠，使得悬臂的形变效果发生了畸变 [11] 。

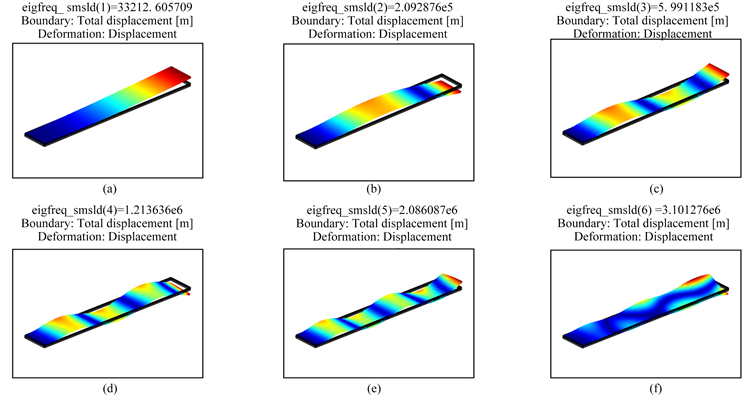
Figure 5. Modal analysis of a cantilever beam model at natural frequencies of 33.2126 KHZ, 209.2876 KHZ, 599.1183 KHZ, 1.2136 MHZ, 2.0861 MHZ, 3.1013 MH

图5. (a)、(b)、(c)、(d)、(e)、(f)分别表示悬臂梁模型在固有频率为33.2126 KHZ、209.2876 KHZ、599.1183 KHZ、1.2136 MHZ、2.0861 MHZ、3.1013 MH的模态

图6分别显示了在总厚度相同和每层厚度相同的条件下，基本频率的变化规律。可以看出，随着介质层数的增加，基本频率逐渐提高，这是由于随着介质层数的增加，等效结构刚度增大，介质层之间的残余应力增大，系统基本频率提高，使得在操作过程中发生共振的可能性相对降低，系统具有更好的动态性能，与文献 [12] 中的报道相一致。两条曲线比较可以得出，对于每层厚度相同的介质模型，由于悬臂的总重量与介质层数成正比，基本频率随着介质层数的增加而线性增加。

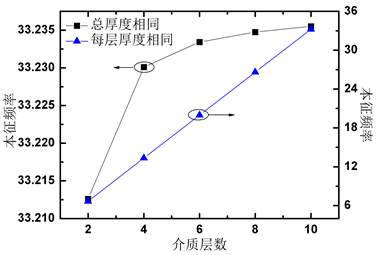
Figure 6. Comparison of Fundamental frequency of cantilever beam models with different dielectric layers (Same total thickness, same thickness for each layer)

图6. 不同介质层数(总厚度相同、每层厚度相同)悬臂梁模型基本频率比较

4. 结论

为了精确表征多介质层悬臂梁结构的机械特性，本文对单层介质模型的结构刚度进行了修正，给出了适合于多层介质的等效结构刚度通式。同时，利用多物理场耦合分析软件COMSOL Multiphysics对多介质层悬臂梁结构进行模拟分析，结果表明，当介质层数从2层增加10层时，等效结构刚度增加了1.9671 N/m，系统的基本频率提高了22 Hz。在相同载荷下，悬臂形变量由2层时的613 nm减小到10层时的544.2 nm。分析得出，随着介质层数的增加，由于各层材料的弹性模量和热膨胀系数不同，层与层之间的形变产生了相互抑制作用，同时各介质层之间存在的静摩擦力产生了粘滞效应，等效结构刚度逐渐增大；固有频率及动态性能随着介质层数的增加而提高。该模拟结果对实际制备过程和性能参数的计算具有十分重要的指导意义，其建模过程同样适用于桥结构和薄膜模型，利用COMSOL Multiphysics模拟分析软件可以直接或间接耦合任意多个物理场的优点，可以分析十分复杂的系统，例如可以在本模型中加入热学模块，对器件的热特性进行进一步分析。