1. 引言
近年来,燃料电池车辆因其具有零污染、低噪声、长续航行驶等优点,已经成为中国车辆工业领域和新能源领域发展的重要技术之一 [1] [2] 。而设计更经济、高效的能量管理策略对燃料电池混合动力车辆(FCHEV, Fuel Cell Hybrid Vehicle)来说也尤为重要,通过优化燃料电池和动力电池输出功率的分配,保证车辆动力性的同时来满足经济性和动力源的耐久性。目前对燃料电池车辆的能量管理策略主要有基于规则和基于优化的策略 [3] [4] ,基于规则的策略主要是依靠相关的工程经验,根据预设逻辑关系以及规则中参数的状态做出相应的控制操作,计算强度低,实用性强,主要包括状态机控制、模糊控制。但简单的规则难以实现同时考虑经济性、能量源耐久性等诸多性能的改善 [5] 。基于优化的策略可以实现多目标优化,但是往往需要知道驾驶工况并且计算量较大 [6] 。庞特里亚金极小值原理(PMP, Pontryagin’s Minimal Principle)是属于优化策略的典型算法,通过建立目标函数,根据已知条件求解系统目标最小的最优解。徐梁飞通过燃料电池瞬时氢耗和动力电池的等效氢耗,建立整车氢气消耗模型,并以此为目标函数,在已知全局工况的情况下求得功率分配的最优解 [7] 。高新梅等提出了使用径向基神经网络预测未来行驶车速的分层能量管理策略,一定程度上解决了优化方法在未知工况下应用较为复杂的难题 [8] 。
因此,本文基于PMP算法,考虑燃料电池混合动力车辆的经济性和动力电池的耐久性之间的平衡,提出一种在未知全局工况下根据动力电池荷电状态(SOC, State of Charge)实时改进的能量管理策略系统。
2. 车辆动力模型
2.1. 整车动力模型
本文中燃料电池混合动力车辆的动力源为燃料电池和动力电池,动力系统结构如图1所示。其中,燃料电池通过单向DC/DC变换器间接连接直流母线、动力电池直接连接直流母线。本文所选车辆参数如表1所示。
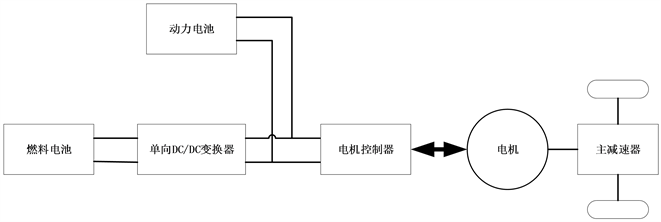
Figure 1. Structure of the vehicle powertrain
图1. 车辆动力系统结构

Table 1. Selected vehicle parameters
表1. 所选车辆参数
根据车辆纵向动力学得出:
(1)
(2)
其中,Ptra为车辆牵引功率,Preq为车辆需求功率,Pb为动力电池功率,Pfc为燃料电池系统净输出功率(后文也简称燃料电池输出功率),m为整车总质量,g为重力加速度,α为坡道角,f为滚动阻力系数,CD为空气阻力系数,A为迎风面积,r为空气密度,v为车辆速度,ƞmot为电机效率,ƞmech为机械传动效率。
2.2. 燃料电池模型
燃料电池堆将氢和氧的化学能转化为电能,不同燃料电池输出功率下氢气消耗的质量流量计算公式由式(3)表示。同时,燃料电池单位时间内的氢耗量由式(3)表示。
(3)
其中,
为燃料电池系统效率,
为氢气低热值(120 kJ/g),
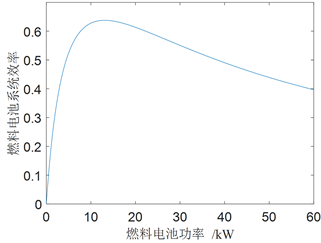
为氢气消耗率。燃料电池系统在不同功率点下的运行效率由实验室数据进行四阶多项式拟合得到。燃料电池效率、单位时间氢耗量与燃料电池输出功率关系如图2所示。
 (a)
(a) 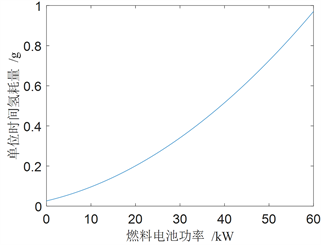 (b)
(b)
Figure 2. FC static output curve: (a) Hydrogen consumption rate curve; (b) Efficiency curve
图2. 燃料电池静态输出曲线:(a) 氢耗量曲线;(b) 效率曲线
2.3. 动力电池模型
本文动力电池模型采用一阶RC锂离子电池等效电路模型,开路电压和充放电内阻与SOC拟合曲线如图3所示。其输出功率可由式(4)表示。
 (a)
(a) 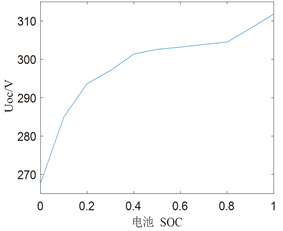 (b)
(b) 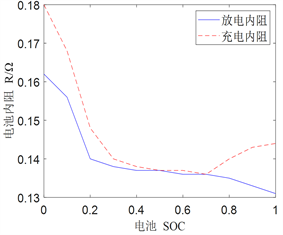 (c)
(c)
Figure 3. Model parameters of Lithium-ion battery: (a) Rint model; (b) Open circuit voltage curve; (c) Resistance curve
图3. 锂离子电池模型参数:(a) Rint模型;(b) 开路电压曲线;(c) 内阻曲线
(4)
其中,Uoc为动力电池开路电压;Rb为动力电池内阻;Pb为动力电池输出功率。则电流Ib可表述为:
(5)
SOC变化率为:
(6)
其中,Qb为电池电荷容量。
3. 庞特里亚金极小值原理
在本文中,主要寻求以最小氢耗量为目标的能量管理策略。因此,利用PMP算法求解最优控制问题中,成本函数定义为:
(7)
其中
为驾驶循环的总时间;
为氢气消耗率;
为燃料电池输出功率。在最优控制问题中,控制变量为燃料电池输出功率,状态变量为动力电池SOC。状态方程为:
(8)
同时动力源需满足以下约束:
(9)
PMP算法中哈密顿函数H定义为:
(10)
其中,λ定义为哈密顿函数中的协态变量。为获得最优燃料电池输出功率的最优轨迹,需满足以下条件:
(11)
(12)
(13)
(14)
其中,*表示最优轨迹;λ表示协态变量。由于SOC的限定范围为0.4~0.8,动力电池的开路电压和电阻几乎不随SOC变化,因此
,即λ始终为一个常量。
因此,可以通过仿真分析在不同的协态变量λ值下得到的动力电池SOC终值,基于此根据
来确定最优协态变量。本文选取三种典型工况HWFET、UDDS、NEDC,分别代表车辆行驶中的高速工况、城市拥挤工况、城市流动工况,如图4所示。通过上述方法,固定初始SOC值为0.6,在不同周期下改变协态变量 常数值,进行了一系列仿真,结果如图5所示。
从图5中可以看出,ΔSOC与协态变量之间的关系是单调的,说明电池的ΔSOC可以通过调节协态变量来调节。当电池SOC值较低时,可以使用较小的协态变量,从而使电池SOC不断上升。当电池SOC
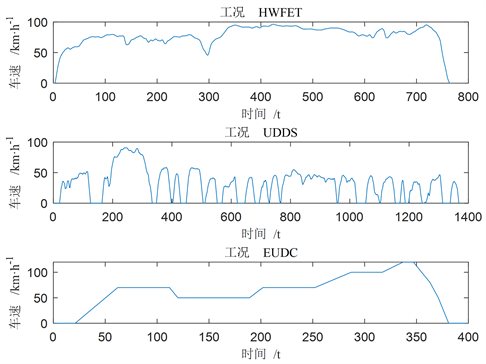
Figure 4. Speed curve under different driving cycle.
图4. 不同工况下速度曲线

Figure 5. The relationship between ΔSOC and constant co-state in different driving cycles
图5. ΔSOC和不同工况下协态变量之间关系曲线
较高时,可以使用较大的协态变量,使电池SOC持续下降。因此,根据电池的SOC,可以实时更新协态变量的值,从而实现PMP的在线应用。本策略希望动力电池SOC维持在0.6左右,0.6是SOC的一个理想值,其既可以保持动力电池处于高效工作区间,也不会因为SOC过大导致能量回收的浪费。如图6所示在HWFET工况下,当初始SOC为0.8时,所期望其ΔSOC为−0.2,因此选择协态变量为−400。当所期望SOC变化量较大的情况下,比如在EUDC工况下,当所期望SOC变化量为0.2时,图6中无法找到合适的最优协态变量,可以选用图中最大的协态变量,如−200,以达到动力电池SOC快速降低的效果,当SOC恢复至可通过调整协态变量来控制SOC变化量时(EUDC工况下为0.4~0.75;UDDS工况下为0.2~0.85),再根据上述图5查询最优协态变量。
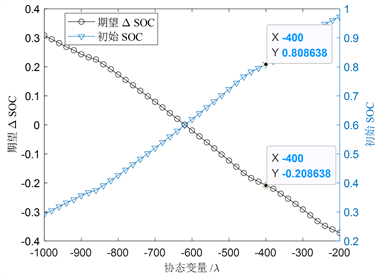
Figure 6. Interpolation curve between the initial SOC and co-state in HWFET cycle.
图6. HWFET工况下协态变量和初始SOC之间插值曲线
4. 实时能量管理策略策略
首先,选取HWFET、UDDS、EUDC工况分别代表车辆高速行驶工况、城市拥挤道路工况、城市流动工况通过提取行驶过程中的特征参数,采用学习矢量量化(LVQ, Learning Vector Quantization)神经网络来进行工况匹配。并根据上一章得到的动力电池初始SOC值与离线数据得到的协态变量与SOC关系曲线,得到最优协态变量。技术路线如图7所示。
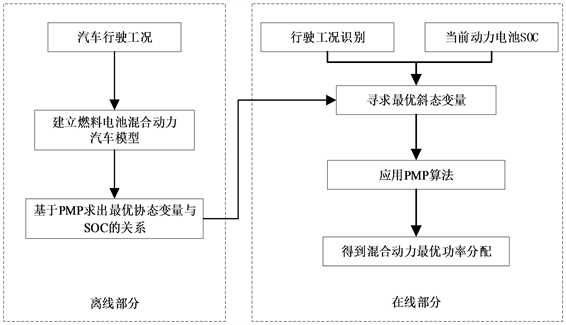
Figure 7. Schematic framework of the real time energy management strategy
图7. 实时能量管理策略的技术路线示意图
本文对上文提出的三种工况采用LVQ神经网络进行训练,LVQ是一种包含训练输入层、隐层和输出层的输出前向神经网络,广泛应用于识别、诊断和优化领域。每个隐层节点代表着一个类别判别中心,如果两个或多个输入向量彼此接近,则隐层将把它们划分为同一类。与其他模式识别相比,LVQ网络比较简单,不需要复杂的神经网络结构,而只需要它们与隐层神经元之间的距离。本文以每10 s为一个片段,片段的平均速度、平均加速度、平均减速度、高速时间所占比例、低速时间所占比例为特征参数。输入神经元设置为5,代表每个片段的5个特征参数,设置隐层数为15个,并设置学习速率为0.01,在1000次训练迭代中,平方误差减少到0.1。为验证该算法有效性,本文选取三个典型工况的片段构建出一个长度1840 s的测试工况进行测试。构建工况及识别结果如图8所示,1代表UDDS工况,2代表EUDC工况,3代表HWFET工况,识别结果准确率达到90%,该算法可用于工况识别。
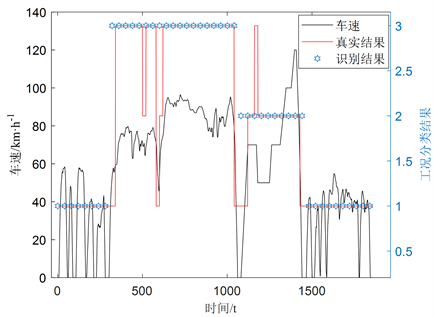
Figure 8. Recognition result of the LVQ network for test cycle
图8. LVQ神经网络对测试工况的识别结果
本文中,确定行驶工况后,将插值曲线应用于控制过程,在每个时间步长中,控制器获得电池的当前SOC,并根据该SOC确定协态变量的值。然后,求解最优的功率分配方法。每60 s执行一次控制过程,仿真结果见图9。该策略并不依赖于对驾驶周期的先验知识。此外,哈密顿函数最小值的解不需要大量的计算资源,因此所提出的能量管理策略可以很容易地应用于实际车辆。

Figure 9. Change curve of SOC under the test cycle
图9. 测试工况下SOC变化曲线
5. 结论
针对燃料电池混合动力车辆,设计了一种基于PMP的在线自适应能量管理策略。首先,通过仿真分析得到了在不同工况下,不同协态变量与SOC变化量之间的关系曲线,发现其呈单调变化,因此可通过插值来确定在不同SOC下协态变量的最优取值。另外针对车辆行驶的三种典型工况(HEFWT、UDDS、EUDC),设计了一种利用LVQ神经网络的工况识别方法,并应用于实时能量管理策略中,以在不同行驶环境下,获得更精确的最优协态变量,将动力电池SOC控制在一定范围内。仿真结果表明,本文所提策略在任何初始SOC条件下,都会将SOC稳定在0.6左右,可保证动力电池处于最优工作效率区间,验证了该方法的有效性。
基金项目
山西省重点研发计划(202102110401020)。
NOTES
*通讯作者。