基于MAP的结合局部和全局统计正则的活动轮廓模型

Active Contour Model Based on MAP Combining Local and Global Statistical Regularization

摘要: 为分割灰度不均匀或者噪声污染的复杂图像，本文提出了一个基于最大后验概率准则(MAP)的结合局部和全局统计正则的活动轮廓模型。首先假设被灰度不均和噪声污染的观测图像服从局部高斯分布；而局部均值图像和局部方差图像在目标和背景区域分别服从全局高斯分布和均匀分布。然后利用3个假设分别构建局部和全局统计正则项，基于MAP准则建立变分活动轮廓模型，并在模型中引入水平集函数的弧长项和H−1正则项，使得水平集函数在演化过程中保持稳定和平滑。最后采用变分法和梯度下降算法对所提的多目标优化模型进行数值求解。数值实验以合成图像和自然图像为实验对象，验证了本文模型对灰度不均和复杂边界的图像具有良好的分割效果，此外还对初始轮廓和噪声鲁棒。并且和几个经典的变分活轮廓模型进行了对比实验，本文模型展示了最优的实验效果。

Abstract: To segment complex images with intensity inhomogeneity or noise pollution, an active contour model based on maximum a posteriori probability (MAP) criterion combining local and global statistical regularity is proposed in this paper. First, it is assumed that the real image obeys a global Gaussian distribution in the background and the object region respectively, while the observed image polluted by intensity inhomogeneity and noise obeys a local Gaussian distribution. Then, the local and global statistical regularization term is constructed using three assumptions, and the variational active contour model is established based on the MAP criterion. The length term and H−1 regularization term of the level set function are introduced into the model, so that the level set function is stable and smooth in the evolution process. Finally, variational method and gradient descent algorithm are used to solve the proposed multi-objective optimization model. Numerical experiments on synthetic and natural images show that the proposed model has good segmentation effect on images with intensity inhomogeneity and complex boundaries, and is robust to initial contour and noise. Compared with several classical variational active contour models, the proposed model has the optimal experimental results.

1. 引言

图像分割是计算机视觉领域的重要内容，已经广泛用于医学图像处理、卫星图像处理、人工智能、目标跟踪与识别等 [1] [2] 。在实际生活中，每一幅图像上都带有一个或多个目标，如何确定目标在图像中的位置，将目标与背景分割开，是人们所研究的问题之一。图像分割就是根据图像的灰度、空间纹理、几何特征等一些属性将图像分为几个子区域，分割的程度取决于要解决的问题。目前，图像分割的方法主要分为两大类：基于传统的分割方法和基于深度学习的分割方法。

基于深度学习的图像分割 [3] [4] ，其基本思想是通过构建多层网络，对目标进行多层表示，以期通过多层的高层次特征来表示数据的抽象语义信息，获得更好的特征鲁棒性。在大量数据集上训练之后，深度学习模型可以分割复杂的图像。但是深度学习在很大程度上仍然是未知领域，没有足够的理论支持，而基于传统的图像分割有着坚实的理论基础，可以用数学的相关知识解释。所以，传统的分割方法仍然受到广大学者的研究。

在传统的分割方法中，基于变分水平集方法的活动轮廓模型已成为当前的研究热点 [5] [6] 。其本质上是用高一维曲面的零等高线作为目标边界去分割低一维的目标，能够很好地处理拓扑结构变换。按照能量函数构造方式的不同，可以将活动轮廓模型分为两大类：基于边缘的模型 [7] [8] [9] 和基于区域的模型 [10] - [21] 。基于边缘的模型依赖于图像的梯度信息，在边界处，图像的梯度较大，所以能够有效地分割具有强边界的图像，但针对弱边界、灰度不均匀的图像分割效果较差。为解决这个问题，一些学者提出了基于区域的活动轮廓模型，该类模型通过区域统计特征来划分图像域，通过区域描述符来定位物体边界。

基于区域的模型通过图像的全局或局部区域信息来构建能量泛函。Chan和Vese [10] (CV)在2001年提出的无边缘活动轮廓模型是经典的基于全局信息的活动轮廓模型之一。该模型能够准确地分割图像中的目标和背景，特别是在简单背景和对比度较高的情况下具有良好效果。并且由于使用水平集函数表示活动轮廓，CV模型可以适应不同形状和大小的目标，并且对初轮廓的选择相对不敏感。但是由于其假设图像的灰度在目标区域和背景区域是均匀的，所以CV模型不能有效地分割灰度不均的图像。为解决此问题，Li等人 [11] 在2008年提出了基于局部二值拟合(Local Binary Fitting, LBF)活动轮廓模型。该模型可以很好地分割灰度不均匀的图像，但是LBF模型对高斯核大小的选取具有依赖性，使得模型很难达到最优效果，且LBF模型对初始轮廓敏感。Wang等人 [12] 在2009年提出了基于局部高斯分布拟合(Local Gaussian Distribution Fitting, LGDF)能量的活动轮廓模型，该模型将具有空间变化的局部均值和方差作为变量，使得LGDF模型能够分割灰度相似但方差不同的区域，但是仍然对初始轮廓比较敏感，加上方差的计算，导致分割速度较慢。上述模型虽然在一定程度上都能够分割灰度不均的图像，但是存在对初始轮廓或噪声敏感等问题。

事实上，除了上述简单地利用图像的全局或局部信息构建的模型之外，一些正则项的加入更符合原始图像的实际信息 [22] [23] [24] [25] 。基于此，Niu等人 [22] 在2017年通过引入一个局部相似因子，使得该模型在保证一定噪声鲁棒性的同时，能够准确提取物体边界。Yan等人 [23] 在2020年提出了一个基于有符号距离函数的凸性形状先验的简单线性不等式约束，使得该模型很容易从背景复杂的图像中分割出凸形目标。Yang等人 [24] 在2021年引入先验约束项，并结合区域可伸缩拟合能量模型，使得该模型具有较高的精度、鲁棒性和有效性。Pang等人 [25] 在2023年提出了基于梯度空间和先验约束的图像分割模型，该模型是在合适的梯度空间下，假设图像是一个分段常数函数和一个平滑函数的乘积。这些正则项的提出在一定程度上提高了模型的分割精度，但是分割边界复杂、严重灰度不均匀的图像仍然是一项巨大的挑战。

为解决此问题，本文提出了一个基于最大后验概率(Maximum A Posteriori Probability, MAP)的结合局部和全局统计正则的活动轮廓模型，实现了对灰度不均匀图像或受噪声污染的复杂图像的理想分割。在该模型中，首先假设灰度不均和被噪声污染的观测图像服从局部高斯分布；而局部均值图像和局部方差图像在目标和背景区域分别服从全局高斯分布和均匀分布。然后基于MAP准则和这3个假设，构建了结合局部和全局统计正则的变分极小化模型。最后结合水平集函数的弧长项和H⁻¹正则项，建立图像分割活动轮廓模型。我们使用交替迭代算法结合变分法和梯度下降法对所提的多目标优化模型进行数值求解。通过对合成图像和真实图像进行仿真实验，验证了本文模型对灰度不均和噪声图像的有效性。

2. 相关背景

2.1. CV模型

Chan和Vese [10] 提出了一个基于区域的模型，考虑了图像的全局信息。设 $I:\Omega \to R$ 是一个给定的图像，轮廓C是一个闭合曲线，将图像分为两个区域：目标区域Ω₁和背景区域Ω₂，该模型的能量泛函定义为：

$\begin{array}{c}{E}^{CV}\left(\varphi ,c_1,c_2\right)={\lambda }_1{\displaystyle {\int }_{\Omega }{\left|I\left(x\right)-c_1\right|}^2{H}_{\epsilon }\left(\varphi \left(x\right)\right)\text{d}x}+{\lambda }_2{\displaystyle {\int }_{\Omega }{\left|I\left(x\right)-c_2\right|}^2\left(1-H_{\epsilon }\left(\varphi \left(x\right)\right)\right)\text{d}x}\\ +\mu {\displaystyle {\int }_{\Omega }^{}\delta \left(\varphi \left(x\right)\right)}\left|\nabla \varphi \left(x\right)\right|\text{d}x+\nu {\displaystyle {\int }_{\Omega }^{}{H}_{\epsilon }\left(\varphi \left(x\right)\right)\text{d}x}\end{array}$ (1)

其中，λ₁、λ₂、ν和μ是正常数， $\varphi \left(x\right)$ 是水平集函数，H(x)是Heaviside函数，δ(x)是Dirac函数，分别定义如下：

$\{\begin{array}{l}{H}_{\epsilon }\left(x\right)=\frac{1}{2}\left(1+\frac{2}{\pi }\arctan \left(\frac{x}{\epsilon }\right)\right)\\ {\delta }_{\epsilon }\left(x\right)={H^{\prime }}_{\epsilon }\left(x\right)=\frac{1}{\pi }\frac{\epsilon }{{\epsilon }^2+x^2}\end{array}$ (2)

c₁和c₂分别表示轮廓内部和外部区域的灰度平均值，根据变分理论和交替迭代法求得变量c₁和c₂的表达式定义为：

$c_1=\frac{{\displaystyle {\int }_{\Omega }I\left(x\right)H\left(\varphi \left(x\right)\right)\text{d}x}}{{\displaystyle {\int }_{\Omega }H\left(\varphi \left(x\right)\right)\text{d}x}},c_2=\frac{{\displaystyle {\int }_{\Omega }I\left(x\right)\left(1-H\left(\varphi \left(x\right)\right)\right)\text{d}x}}{{\displaystyle {\int }_{\Omega }\left(1-H\left(\varphi \left(x\right)\right)\right)\text{d}x}}$ (3)

对变量 $\varphi \left(x\right)$ ，使用梯度下降方法求解。固定c₁和c₂， $E^{CV}\left(\varphi ,c_1,c_2\right)$ 关于 $\varphi \left(x\right)$ 的极小值为以下演化方程的稳态解：

$\frac{\partial \varphi }{\partial t}={\delta }_{\epsilon }\left(\varphi \right)\left[-{\lambda }_1{\left(I\left(x\right)-c_1\right)}^2+{\lambda }_2{\left(I\left(x\right)-c_2\right)}^2+\mu div\left(\frac{\nabla \varphi }{\left|\nabla \varphi \right|}\right)-\nu \right]$ (4)

CV模型考虑了整个图像的全局信息，能够对整体目标进行较好地分割。并且它不依赖于任何先验知识或特定领域的信息。但是当图像存在灰度不均匀情况时，CV模型可能会受到较亮或较暗区域的影响，导致轮廓收缩或扩张过程中无法运动到正确的目标边界，这可能会导致分割结果出现断裂、漏分割或误分割等问题。

2.2. LBF模型

为了克服CV模型的缺点，Li等人 [11] 提出了基于局部区域信息的LBF模型，该模型利用高斯核函数的局部特性提取图像的局部信息，能够有效地分割灰度不均的图像。能量泛函定义如下：

$\begin{array}{c}{E}^{LBF}\left(\varphi ,f_1\left(x\right),f_2\left(x\right)\right)={\lambda }_1{\displaystyle \int {\displaystyle \int K_{\sigma }\left(x-y\right){\left|I\left(y\right)-f_1\left(x\right)\right|}^{2}H\left(\varphi \left(y\right)\right)\text{d}x\text{d}y}}\\ +{\lambda }_2{\displaystyle \int {\displaystyle \int K_{\sigma }\left(x-y\right){\left|I\left(y\right)-f_2\left(x\right)\right|}^2\left(1-H\left(\varphi \left(y\right)\right)\right)\text{d}x\text{d}y}}\end{array}$ (5)

其中，λ₁和λ₂是正常数，f₁(x)和f₂(x)是两个空间变化的拟合函数，分别近似于活动轮廓内外区域的局部灰度均值，K_σ(u)是高斯核函数，定义如下：

$K_{\sigma }\left(x\right)=\frac{1}{{\left(2\pi \right)}^{n/2}\sigma }{\text{e}}^{-{\left|x\right|}^2/2{\sigma }^2}$ (6)

为了使活动轮廓在演化过程中保持平滑性与稳定性，该模型又加入了长度正则项和符号距离函数约束正则项，分别定义如下：

$L\left(\varphi \right)={\displaystyle {\int }_{\Omega }^{}\delta \left(\varphi \left(x\right)\right)}\left|\nabla \varphi \left(x\right)\right|\text{d}x$ (7)

$D\left(\varphi \right)={\displaystyle {\int }_{\Omega }^{}\frac{1}{2}}{\left(\left|\nabla \varphi \left(x\right)\right|-1\right)}^2\text{d}x$ (8)

其中长度正则项 $L\left(\varphi \right)$ 是为了使水平集轮廓在演化过程中保持光滑，使得分割结果尽可能少地出现面积小的孤立分割区域。距离正则项 $D\left(\varphi \right)$ 是为了使活动轮廓在演化过程中保持稳定，避免重新初始化。

最后，模型的总能量泛函定义为：

$E_{all}^{LBF}\left(\varphi ,f_1\left(x\right),f_2\left(x\right)\right)=E^{LBF}\left(\varphi ,f_1\left(x\right),f_2\left(x\right)\right)+\mu L\left(\varphi \right)+vD\left(\varphi \right)$ (9)

固定水平集函数 $\varphi$ ，关于式(5)使用变分法求得f₁(x)和f₂(x)定义如下：

$\{\begin{array}{l}{f}_1\left(x\right)=\frac{K_{\sigma }\ast \left[H\left(\varphi \right)I\left(x\right)\right]}{K_{\sigma }\ast H\left(\varphi \right)}\\ f_2\left(x\right)=\frac{K_{\sigma }\ast \left[\left(1-H\left(\varphi \right)\right)I\left(x\right)\right]}{K_{\sigma }\ast (1-H(\; \varphi \; ))}\end{array}$

固定f₁(x)和f₂(x)，利用变分法和梯度下降法，求式(9)关于水平集函数 $\varphi$ 的梯度下降流为：

$\frac{\partial \varphi }{\partial t}=-\delta \left(\varphi \right)\left({\lambda }_1{e}_1-{\lambda }_2{e}_2\right)+\mu \delta \left(\varphi \right)div\left(\frac{\nabla \varphi }{\left|\nabla \varphi \right|}\right)+v\left({\nabla }^2\varphi -div\left(\frac{\nabla \varphi }{\left|\nabla \varphi \right|}\right)\right)$ (10)

其中e₁(x)和e₂(x)表示为：

$\{\begin{array}{l}{e}_1\left(x\right)={\displaystyle {\int }_{\Omega }{K}_{\sigma }\left(y-x\right)}{\left|I\left(x\right)-f_1\left(y\right)\right|}^2\text{d}y\\ e_2\left(x\right)={\displaystyle {\int }_{\Omega }{K}_{\sigma }\left(y-x\right)}{\left|I\left(x\right)-f_2\left(y\right)\right|}^2\text{d}y\end{array}$

LBF模型考虑了图像的局部信息，能够有效地分割灰度不均图像。但该模型在一定程度上对初始轮廓和噪声敏感，而且对于高斯核函数的尺度参数的选择并没有统一标准，所以较难达到最优效果。

3. 本文方法

3.1. 模型假设

设 $I\left(x\right):\Omega \to R$ 是一幅给定的观测图像，Ω₁和Ω₂满足 ${\Omega }_1\cap {\Omega }_{\text{2}}=\varnothing ，{\Omega }_1\cup {\Omega }_{\text{2}}=\Omega$ ，分别代表图像的目标和背景区域。下面我们针对观测图像I(x)给定以下3个假设，分别表述如下。这3个假设将在后续的建模中起关键作用。

(1) 由于观测图像I(x)受到灰度不均和噪声的影响，在目标Ω₁和背景Ω₂区域中不满足全局高斯分布，但是我们假设其满足局部高斯分布，即对 $y\in {\Omega }_i\cap O_x$ ，其中O_x表示以x为中心的局部邻域，定义为 $O_x\triangleq \left\{y:\left|x-y\right|\le \delta \right\}$ ，满足

$I\left(y\right)\sim N\left(u_i\left(x\right),{\sigma }_i^2(\; x\; )\right)$

其中 $N\left(u_i\left(x\right),{\sigma }_i^2\left(x\right)\right)$ 表示以u_i(x)为均值， ${\sigma }_i^2\left(x\right)$ 为方差的高斯分布。

(2) 假设局部均值图像u_i(x)在目标Ω₁和背景Ω₂区域中分别服从全局高斯分布，即对 $x\in {\Omega }_i$ ，满足

$u_i\left(x\right)\sim N\left(c_i,{\sigma }_i^2\right)$

其中 $N\left(c_i,{\sigma }_i^2\right)$ 表示以c_i为均值， ${\sigma }_i^2$ 为方差的高斯分布。

(3) 假设局部方差 ${\sigma }_i^2\left(x\right)$ 在目标Ω₁和背景Ω₂区域中服从的均匀分布，即

$p\left({\sigma }_i^2\left(x\right)\right)=C_i$

3.2. 模型构建

在本节中，我们根据贝叶斯公式并利用MAP准则，通过观测图像I(x)对两个高斯分布的数字特征 ${\theta }_1\left(x\right)=\left(u_i\left(x\right),{\sigma }_i^2\left(x\right)\right)$ 和 ${\theta }_2=\left(c_i,{\sigma }_i^2\right)$ 进行估计：

$p\left({\theta }_1\left(x\right),{\theta }_2|I\left(x\right)\right)=\frac{p\left(I\left(x\right)|{\theta }_1\left(x\right),{\theta }_2\right)p\left({\theta }_1\left(x\right)|{\theta }_2\right)p\left({\theta }_2\right)}{p\left(I\left(x\right)\right)}$ (11)

其中， $p\left(I\left(x\right)|{\theta }_1\left(x\right),{\theta }_2\right)$ 是似然函数，表示特征图像和观测图像I(x)的关联程度， $p\left({\theta }_1\left(x\right)|{\theta }_2\right)$ 是局部特征的概率密度， $p\left({\theta }_2\right)$ 和 $p\left(I\left(x\right)\right)$ 分别表示灰度值I(x)和θ₂的先验概率，在MAP准则下，我们将其忽略。式(11)可以重写为：

$p\left({\theta }_1\left(x\right),{\theta }_2|I\left(x\right)\right)\propto p\left(I\left(x\right)|{\theta }_1\left(x\right),{\theta }_2\right)p\left({\theta }_1\left(x\right)|{\theta }_2\right)$ (12)

接下来，我们将根据上述3条假设分别对 $p\left(I\left(x\right)|{\theta }_1\left(x\right),{\theta }_2\right)$ 和 $p\left({\theta }_1\left(x\right)|{\theta }_2\right)$ 进行计算。

(1) 计算似然函数 $p\left(I\left(x\right)|{\theta }_1\left(x\right),{\theta }_2\right)$

根据假设1，在图像域中，对每个点 $x\in {\Omega }_i$ ，考虑一个半径为δ的圆形邻域，定义为 $O_x\triangleq \left\{y:\left|x-y\right|\le \delta \right\}$ ，对 $\forall y\in {\Omega }_i\cap O_x$ ， $p\left(I\left(y\right)|{\theta }_1\left(x\right),{\theta }_2\right)$ 是观测图像I(y)的一个似然概率。由于观测图像服从局部高斯分布，所以由贝叶斯公式得到：

$p\left(I\left(y\right)|{\theta }_1\left(x\right),{\theta }_2\right)=\frac{1}{\sqrt{2\pi }{\sigma }_i\left(x\right)}\exp \left(-\frac{{\left(I\left(y\right)-u_i\left(x\right)\right)}^2}{2{\sigma }_i^2\left(x\right)}\right)$ (13)

其中，u_i(x)和σ_i(x)是局部灰度均值和方差。

接下来，我们计算在整个图像域中的 $p\left(I\left(x\right)|{\theta }_1\left(x\right),{\theta }_2\right)$ ，对 $\forall y\in {\Omega }_i\cap O_x,i=1,2$ 和 $x\in \Omega$ ，

$\begin{array}{c}p\left(I\left(x\right)|{\theta }_1\left(x\right),{\theta }_2\right)={\displaystyle \underset{x\in \Omega }{\prod }{\displaystyle \underset{i=1}{\overset{2}{\prod }}{\displaystyle \underset{y\in {\Omega }_i\cap O_x}{\prod }p\left(I\left(y\right)|{\theta }_1\left(x\right),{\theta }_2\right)}}}\\ ={\displaystyle \underset{x\in \Omega }{\prod }{\displaystyle \underset{i=1}{\overset{2}{\prod }}{\displaystyle \underset{y\in {\Omega }_i\cap O_x}{\prod }\frac{1}{\sqrt{2\pi }{\sigma }_i\left(x\right)}\exp \left(-\frac{{\left(I\left(y\right)-u_i\left(x\right)\right)}^2}{2{\sigma }_i^2\left(x\right)}\right)}}}\end{array}$ (14)

为了提高模型效率，减少计算时间，我们只对图像的灰度值特征进行建模，将含 $1/{\sigma }_i\left(x\right)$ 和 ${\sigma }_i^2\left(x\right)$ 的一部分看作一个常值，因此式(14)可以重写为：

$p\left(I\left(x\right)|{\theta }_1\left(x\right),{\theta }_2\right)={\displaystyle \underset{x\in \Omega }{\prod }{\displaystyle \underset{i=1}{\overset{2}{\prod }}{\displaystyle \underset{y\in {\Omega }_i\cap O_x}{\prod }\frac{1}{Z_{1i}}\exp \left(-\frac{{\left(I\left(y\right)-u_i\left(x\right)\right)}^2}{Z_{2i}}\right)}}}$ (15)

(2) 计算局部特征图像概率 $p\left({\theta }_1\left(x\right)|{\theta }_2\right)$

在本文中，由于 ${\theta }_1\left(x\right)=\left(u_i\left(x\right),{\sigma }_i^2\left(x\right)\right)$ ，我们可得

$p\left({\theta }_1\left(x\right)|{\theta }_2\right)=p\left(u\left(x\right)|{\theta }_2\right)p\left(\sigma \left(x\right)|{\theta }_2\right)$

由假设3，局部方差 ${\sigma }_i^2\left(x\right)$ 在目标Ω₁和背景Ω₂区域中服从的均匀分布，则可得

$p\left({\theta }_1\left(x\right)|{\theta }_2\right)\propto p\left(u\left(x\right)|{\theta }_2\right)$ (16)

下面计算 $p\left(u\left(x\right)|{\theta }_2\right)$ ，针对局部均值图像u(x)，我们考虑了图像的全局统计信息，由假设2，局部均值图像u(x)在目标Ω₁和背景Ω₂区域中分别服从全局高斯分布，所以对 $x\in {\Omega }_i,i=1,2$ ， $p\left(u_i\left(x\right)|{\theta }_2\right)$ 定义如下：

$p\left(u_i\left(x\right)|{\theta }_2\right)=\frac{1}{\sqrt{2\pi }{\sigma }_i}\exp \left(-\frac{{\left(u_i\left(x\right)-c_i\right)}^2}{2{\sigma }_i^2}\right)$

其中c_i定义如上式(3)。因为方差是衡量数据离散程度的一个指标，其大小变化影响图像的灰度值分布。在本文模型中，为简化计算，我们将含 $1/{\sigma }_i$ 和 ${\sigma }_i^2$ 的一部分看作一个常值。则在整个图像域中 $p\left(u\left(x\right)|{\theta }_2\right)$ 定义为：

$p\left(u\left(x\right)|{\theta }_2\right)={\displaystyle \underset{i=1}{\overset{2}{\prod }}{\displaystyle \underset{x\in {\Omega }_i}{\prod }\frac{1}{T_{1i}}\exp \left(-\frac{{\left(u_i\left(x\right)-c_i\right)}^2}{T_{2i}}\right)}}$ (17)

概率分布 $p\left(u\left(x\right)|{\theta }_2\right)$ 为局部均值图像u(x)提供了全局灰度分布的先验信息，使得模型更为精细，更好的建模了灰度不均和噪声污染图像。接下来，结合式(12)、式(15)和式(17)，我们得到：

$\begin{array}{c}p\left({\theta }_1\left(x\right),{\theta }_2|I\left(x\right)\right)\propto {\displaystyle \underset{x\in \Omega }{\prod }{\displaystyle \underset{i=1}{\overset{2}{\prod }}{\displaystyle \underset{y\in {\Omega }_i\cap O_x}{\prod }p\left(I\left(y\right)|{\theta }_1\left(x\right),{\theta }_2\right)}}}{\displaystyle \underset{i=1}{\overset{2}{\prod }}{\displaystyle \underset{x\in {\Omega }_i}{\prod }p\left({\theta }_1\left(x\right)|{\theta }_2\right)}}\\ ={\displaystyle \underset{x\in \Omega }{\prod }{\displaystyle \underset{i=1}{\overset{2}{\prod }}{\displaystyle \underset{y\in {\Omega }_i\cap O_x}{\prod }\frac{1}{Z_{1i}}\exp \left(-\frac{{\left(I\left(y\right)-u_i\left(x\right)\right)}^2}{Z_{2i}}\right)}}}\\ \times {\displaystyle \underset{i=1}{\overset{2}{\prod }}{\displaystyle \underset{x\in {\Omega }_i}{\prod }\frac{1}{T_{1i}}\exp \left(-\frac{{\left(u_i\left(x\right)-c_i\right)}^2}{T_{2i}}\right)}}\end{array}$ (18)

利用MAP准则，并且对上式取对数，可将最大值转换为以下能量的最小值，表示为：

$\begin{array}{c}\underset{{\Omega }_i,u(x),c}{\min }E=E^L+E^G\\ ={\displaystyle \underset{i=1}{\overset{2}{\sum }}{\displaystyle {\int }_{x\in \Omega }{\displaystyle {\int }_{y\in {\Omega }_i\cap O_x}-\log }}}p\left(I\left(y\right)|{\theta }_1\left(x\right),{\theta }_2\right)\text{d}x\text{d}y+{\displaystyle \underset{i=1}{\overset{2}{\sum }}{\displaystyle {\int }_{x\in {\Omega }_i}-p\left({\theta }_1\left(x\right)|{\theta }_2\right)\text{d}x\text{d}y}}\\ ={\displaystyle \underset{i=1}{\overset{2}{\sum }}{\lambda }_i{\displaystyle {\int }_{x\in \Omega }{\displaystyle {\int }_{y\in {\Omega }_i\cap O_x}{\left(I\left(y\right)-u_i\left(x\right)\right)}^2}}}\text{d}x\text{d}y+{\displaystyle \underset{i=1}{\overset{2}{\sum }}{\alpha }_i{\displaystyle {\int }_{x\in {\Omega }_i}{\left(u_i\left(x\right)-c_i\right)}^2}}\text{d}x\text{d}y\end{array}$ (19)

其中， ${\lambda }_i=\frac{\log Z_{1i}}{Z_{2i}}$ ， ${\alpha }_i=\frac{\log T_{1i}}{T_{2i}},i=1,2$ 。

3.3. 水平集函数

下面利用水平集技术，结合Heaviside函数和高斯核函数，将式(19)的积分区域扩充到整个图像区域Ω，则(19)可以改写为：

$\begin{array}{c}\underset{\varphi ,u(x),c}{\min }E=E^L+E^G\\ ={\displaystyle \underset{i=1}{\overset{2}{\sum }}{\lambda }_i{\displaystyle {\iint }_{\Omega }{K}_{\sigma }\left(x-y\right){\left(I\left(y\right)-u_i\left(x\right)\right)}^2{M}_i\left(\varphi \right)\text{d}x\text{d}y}}\\ +{\displaystyle \underset{i=1}{\overset{2}{\sum }}{\alpha }_i{\displaystyle {\int }_{\Omega }{\left(u_i\left(x\right)-c_i\right)}^2{M}_i\left(\varphi \right)\text{d}x\text{d}y}}\end{array}$ (20)

其中， $K_{\sigma }\left(x-y\right)$ 是高斯核函数，等价于局部区域O_x的指示函数，定义如(6)式所示； $M_1=H\left(\varphi \right)$ 和 $M_2=1-H\left(\varphi \right)$ 分别表示Ω₁和Ω₂的指示函数。

与典型的水平集方法一样，为了使水平集轮廓在演化过程中保持光滑，使分割结果尽可能少地出现面积小的孤立区域，我们通过惩罚其弧长来使演化曲线保持正则化，长度项的定义如上式(7)。此外，为了防止水平集函数在演化过程中变得过于陡峭或出现震荡等不稳定情况，我们又加入了H⁻¹正则项，用来对水平集函数进行平滑处理，具体定义如下：

$R\left(\varphi \right)={\displaystyle {\int }_{\Omega }{\left|\nabla \varphi \left(x\right)\right|}^2}\text{d}x$ (21)

最后，结合数据项(20)和水平集函数的正则项，得到如下的能量泛函：

$\begin{array}{c}{E}_{all}=E^L+E^G+\mu L\left(\varphi \right)+R\left(\varphi \right)\\ ={\displaystyle \underset{i=1}{\overset{2}{\sum }}{\lambda }_i{\displaystyle {\iint }_{\Omega }{K}_{\sigma }\left(x-y\right){\left(I\left(y\right)-u_i\left(x\right)\right)}^2{M}_i\left(\varphi \right)\text{d}x\text{d}y}}\\ +{\displaystyle \underset{i=1}{\overset{2}{\sum }}{\alpha }_i{\displaystyle {\int }_{\Omega }{\left(u_i\left(x\right)-c_i\right)}^2{M}_i\left(\varphi \right)\text{d}x\text{d}y}}\\ +\mu {\displaystyle {\int }_{\Omega }^{}\delta \left(\varphi \left(x\right)\right)}\left|\nabla \varphi \left(x\right)\right|\text{d}x+{\displaystyle {\int }_{\Omega }{\left|\nabla \varphi \left(x\right)\right|}^2}\text{d}x\end{array}$ (22)

当水平集函数偏离目标边界时，局部灰度均值u_i(x)和全局灰度均值c_i之间存在较大的差距；当水平集函数接近目标边界时，u_i(x)和c_i之间的差距较小；当水平集函数正好位于目标边界时，u_i(x)和c_i相等，此时，能量泛函中E^L项能量达到最小。

3.4. 模型求解

本文采用交替迭代算法对模型进行求解。对于一个固定的水平集函数，我们关于u₁(x)和u₂(x)最小化能量泛函E_all。通过变分法，函数u₁(x)和u₂(x)分别满足以下两个Euler-Lagrange方程：

${\lambda }_1{\displaystyle \int K_{\sigma }\left(x-y\right)}{\left|I\left(y\right)-u_1\left(x\right)\right|}^{2}H\left(\varphi \right)\text{d}y+{\alpha }_1{\left(u_1\left(x\right)-c_1\right)}^{2}H\left(\varphi \right)=0$ (23)

${\lambda }_2{\displaystyle \int K_{\sigma }\left(x-y\right)}{\left|I\left(y\right)-u_2\left(x\right)\right|}^2\left(1-H\left(\varphi \right)\right)\text{d}y+{\alpha }_2{\left(u_2\left(x\right)-c_2\right)}^2\left(1-H\left(\varphi \right)\right)=0$ (24)

从式(23)和式(24)分别求解出函数u₁(x)和u₂(x)，可以得到：

$\{\begin{array}{l}{u}_1\left(x\right)=\frac{{\alpha }_1{c}_{1}H\left(\varphi \right)+{\lambda }_1{\displaystyle \int K_{\sigma }\left(x-y\right)I\left(y\right)H\left(\varphi \right)\text{d}y}}{{\alpha }_{1}H\left(\varphi \right)+{\lambda }_1{\displaystyle \int K_{\sigma }\left(x-y\right)H\left(\varphi \right)\text{d}y}}\\ u_2\left(x\right)=\frac{{\alpha }_2{c}_2\left(1-H\left(\varphi \right)\right)+{\lambda }_2{\displaystyle \int K_{\sigma }\left(x-y\right)I\left(y\right)\left(1-H\left(\varphi \right)\right)\text{d}y}}{{\alpha }_2\left(1-H\left(\varphi \right)\right)+{\lambda }_2{\displaystyle \int K_{\sigma }\left(x-y\right)\left(1-H\left(\varphi \right)\right)\text{d}y}}\end{array}$ (25)

保持u₁(x)和u₂(x)固定，并使能量泛函E_all关于 $\varphi$ 最小化，采用变分法和梯度下降法，我们推导出梯度下降流方程：

$\begin{array}{c}\frac{\partial \varphi }{\partial t}=-\delta \left(\varphi \right)\left[{\lambda }_1{\displaystyle {\int }_{\Omega }{K}_{\sigma }\left(x-y\right)}{\left|I\left(y\right)-u_1\left(x\right)\right|}^2\text{d}x\right]\\ +\delta \left(\varphi \right)\left[{\lambda }_2{\displaystyle {\int }_{\Omega }{K}_{\sigma }\left(x-y\right)}{\left|I\left(y\right)-u_2\left(x\right)\right|}^2\text{d}x\right]\\ +\delta \left(\varphi \right)\left({\alpha }_1{\left(u_1\left(x\right)-c_1\right)}^2-{\alpha }_2{\left(u_2\left(x\right)-c_2\right)}^2\right)\\ +\mu \delta \left(\varphi \right)div\left(\frac{\nabla \varphi }{\left|\nabla \varphi \right|}\right)+\Delta \varphi \end{array}$ (26)

本文采用有限差分法对(26)式进行数值求解。综上，交替迭代算法求解本文模型的具体算法步骤如下：

4. 数值实验

本文提出的模型是在MATLAB 2020b中实现，运行在Intel(R) Core(TM) i5-8265U CPU @ 3.2GHz的系统上。实验首先验证本文模型的有效性，其次验证本文模型对初始轮廓的鲁棒性和对噪声的鲁棒性，最后与CV [10] 、LBF [11] 、LIC [18] 、GLFIF [19] 模型进行对比实验。

(a)

(b)

Figure 1. The segmentation experiment of the model in this paper. (a) Segmentation of synthetic images or medical images; (b) Segmentation of natural images

图1. 本文模型的分割实验。(a) 分割合成图像或医学图像；(b) 分割自然图像

4.1. 评价指标

为了对模型的分割效果进行定量分析，我们引入了Dice相似系数(DSC)，其定义如下：

$DSC=\frac{2\left(S_T\cap S_E\right)}{S_T+S_E}$

其中，S_T表示真值图，S_E表示实验获得的分割图。DSC的值越接近1，代表分割精度越高。

4.2. 模型的有效性

为了验证本文模型的有效性，我们对10幅不同的图像进行了分割实验。图1中(a)是合成图像或医学图像的分割，(b)是自然图像的分割结果。(a)和(b)的第一行是带初始轮廓的原始图像，第二行是分割结果，第三行是分割轮廓。从实验结果可以看出，本文模型可以有效地分割灰度不均、边界模型、对比度低的图像。

4.3. 模型对初始轮廓和噪声的鲁棒性

本节验证模型对初始轮廓的鲁棒性。选取3幅图像进行实验，如图2，绿色曲线代表初始轮廓，红色曲线代表分割结果。实验结果表明，初始轮廓无论是在分割目标上，还是在背景上，最终都可以准确地定位到目标边界，得到理想的分割结果。因此，本文模型对初始轮廓位置具有鲁棒性。

Figure 2. Image segmentation results with different initial contours

图2. 具有不同初始轮廓的图像分割结果

下面验证模型对噪声的鲁棒性。如图3，第一行到第三行分别添加均值为0，不同方差的高斯白噪声；不同密度的椒盐噪声；均值为0，不同方差的光斑噪声的图像分割结果。第一列是原始图像分割结果，第二列到第六列分别是添加了不同强度的噪声图像的分割结果。从实验结果可以看出，对于单一噪声污染的图像，本文模型能够有效地排除噪声的影响，准确地捕捉到目标物体的轮廓。

${\sigma }^2=0$ ${\sigma }^2=0.01$ ${\sigma }^2=0.05$ ${\sigma }^2=0.1$ ${\sigma }^2=0.2$ ${\sigma }^2=0.3$

$\rho =0$ $\rho =0.01$ $\rho =0.05$ $\rho =0.1$ $\rho =0.2$ $\rho =0.3$ ${\sigma }^2=0$ ${\sigma }^2=0.01$ ${\sigma }^2=0.05$ ${\sigma }^2=0.1$ ${\sigma }^2=0.2$ ${\sigma }^2=0.3$

Figure 3. The segmentation results of noisy images

图3. 噪声图像分割结果

(a) (b) (c) (d) (e) (f)

Figure 4. The segmentation results of hybrid noise image

图4. 混合噪声图像分割结果

图4展示了6幅混合噪声图像的分割结果。在这6幅图像中分别依次添加不同类型的噪声，以此来验证本文模型对混合噪声图像的有效性。(a)~(c)依次添加了密度为0.1的椒盐噪声、均值为0，方差为0.05的高斯白噪声和均值为0，方差为0.1的光斑噪声。(d)~(f)依次添加了密度为0.01的椒盐噪声、均值为0，方差为0.01的高斯白噪声和均值为0，方差为0.01的光斑噪声。分割结果表明，本文模型对混合噪声图像的分割具有很强的鲁棒性。

${\sigma }^2=0$ ${\sigma }^2=0.01$ ${\sigma }^2=0.025$ ${\sigma }^2=0.05$ ${\sigma }^2=0.075$ ${\sigma }^2=0.1$

(a)

$\rho =0$ $\rho =0.01$ $\rho =0.025$ $\rho =0.05$ $\rho =0.075$ $\rho =0.1$

(b)

${\sigma }^2=0$ ${\sigma }^2=0.01$ ${\sigma }^2=0.025$ ${\sigma }^2=0.05$ ${\sigma }^2=0.075$ ${\sigma }^2=0.1$(c)

Figure 5. Noise comparison experiment between LBF model and this model. (a) Comparison experiment of Gaussian white noise; (b) Comparison experiment of salt and pepper noise; (c) Comparison experiment of spot noise

图5. LBF模型和本文模型的噪声对比实验。(a) 高斯白噪声对比实验；(b) 椒盐噪声对比实验；(c) 光斑噪声对比实验

为进一步验证本文模型对噪声的鲁棒性，我们在灰度不均匀的图像中添加不同类型的噪声来实现对噪声图像的分割，并与LBF模型进行对比实验。

图5(a)、图5(b)、图5(c)分别是LBF模型和本文模型对零均值高斯白噪声、椒盐噪声和零均值光斑噪声的分割结果的比较。图5(a)、图5(b)和图5(c)的第一行是LBF模型的分割结果，第二行是本文模型的分割结果。第一列是带有初始轮廓的原始图像的分割结果，第二列到第六列是分别添加了不同等级噪声的分割结果。在分割过程中，保持初始轮廓和参数不变，只改变迭代次数，迭代次数和分割时间如表1所示。由实验结果可以看出，LBF模型能够成功地分割出含低程度的噪声图像，但是在噪声水平较高的情况下，不能准确地定位目标边界，而且分割所需要的时间较长；本文模型能够在不同等级的噪声下精确地分割图像，且需要的迭代次数和时间比LBF模型更具优势，所以本文模型对噪声具有鲁棒性。

Table 1. Comparison of number of interations N and segmentation time S (N/S)

表1. 迭代次数N和分割时间S对比(N/S)

4.4. 不同模型的对比实验

原图 CV LBF LICGLFIF OUR

Figure 6. Results of bimodal image segmentation by different models

图6. 不同模型分割双峰图像的结果

本节我们选取不同类型的图像进行分割对比实验。图6是双峰图像的分割结果，第一列是原始图像，第二列到第六列分别是CV、LBF、LIC、GLFIF和本文模型的分割结果。实验结果表明，所有方法都对这些双峰图像的分割有着较好的效果。但是，如表2所示，本文模型只需迭代1次，就能得到良好的分割效果，对比其他模型的分割时间可以看出，本文模型无论是在迭代次数还是分割时间上都优于其它对比模型。

Table 2. Iteration times N and segmentation time S (N/S)

表2. 迭代次数N和分割时间S (N/S)

为验证本文模型对灰度不均匀图像的分割效果，我们选取了4幅典型的合成或医学图像进行对比实验，这4幅图像具有严重灰度不均、边界弱、对比度低以及光照不均匀等问题。图7的第一列是原始图像，第二列到第六列对比模型的分割结果。从实验结果可以看出，CV、LIC和GLFIF模型对灰度不均匀的图像分割效果较差，LBF模型可以分割部分灰度不均的图像，本文模型对灰度不均的图像分割效果较好。结合表3中的数据，可以看出本文提出的模型不仅可以准确地定位目标边界，还可以在较短的时间内实现理想的分割效果。

原图 CV LBF LIC GLFIF OUR

Figure 7. The results of segmentation of intensity inhomogeneity image by different models

图7. 不同模型分割灰度不均匀图像的结果

Table 3. Iteration times N and segmentation time S (N/S)

表3. 迭代次数N和分割时间S (N/S)

图8是为验证本文模型对自然图像的有效性。我们选中6幅灰度不均的自然图像进行对比实验，第一列是原图，第二列是分割真值图，第三列到第七列分别是CV、LBF、LIC、GLFIF和本文模型的分割结果。从图中可以观察到，对于背景较简单的图像，如第一行和第二行，本文模型和对比模型都可以定位到目标边界，但是从分割的最终分割轮廓可以看出本文模型的分割效果最好；对于背景较复杂的图像，如第三行到第六行，CV、LIC和GLFIF模型都不能准确地分割目标，LBF可以分割部分图像，本文模型在分割复杂背景的图像时也能得到较好的分割结果。结合图8和图9，可以看出，我们的模型可以实现对复杂图像的分割，且DSC值都优于文中的其它对比模型。

原图真值图 CV LBF LIC GLFIF OUR

Figure 8. Comparative experimental results of different models

图8. 不同模型的对比实验结果

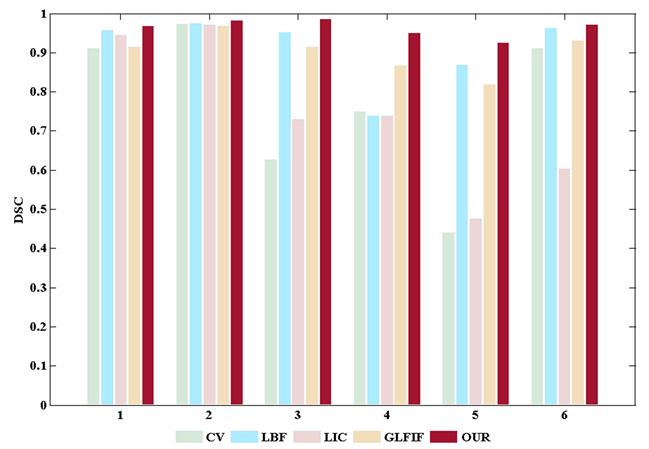
Figure 9. Experimental comparison of DSC values

图9. DSC值实验对比

5. 结论

为了更好地分割灰度不均匀和噪声污染的图像，本文提出了一个基于MAP的全局和局部统计先验活动轮廓模型。该模型通过假设观测图像服从局部高斯分布；而局部均值图像和局部方差图像分别服从全局高斯分布和均匀分布。根据这3个假设，基于MAP准则，构建了结合局部和全局信息的变分活动轮廓模型。实验结果表明，本文模型不仅具有较高的分割效率，还对初始轮廓和噪声鲁棒。然而，我们注意到，在实验过程中参数较多，且对参数的选取没有统一标准，因此如何减少参数对最终分割结果的影响是我们下一步关注的内容。

基金项目

国家自然科学基金项目资助(模糊正则化图像复原及深度网络学习实现研究62061016，非凸非光滑高阶变分正则和非局部变分正则图像复原研究61561019)。

NOTES

^*通讯作者。