1. 引言
近几十年来,雷达的发展日新月异,在军用和民用两个领域中雷达均成为了环境感知和目标探测的重要核心设备。因为阵列天线的可靠性、可拓展性以及对波束的灵活控制,使得阵列天线作为接收/发射天线广泛应用于各种类型的雷达。随着阵列天线的应用,传统雷达的信号处理方法不能发挥出阵列天线的优势,阵列信号处理技术应运而生,其中,波达方向(Direction of Arrival, DOA)估计 [1] [2] [3] 更是阵列信号处理的重要组成部分。DOA估计通过多个传感器阵元共同采样来波信号接收阵列数据,实现对有用信号进行增强、对噪声信息进行抑制的目的,最终估计信号的波达方向角度。随着DOA估计技术性能的提高,其应用领域也在迅速发展。对空间多个来波信号进行高精度的测向符合国防及民生众多行业部门的迫切需求,同时赋予了DOA估计重大的研究意义 [1] [2] [3] 。
基于特征分解方法的DOA估计是一个活跃的研究领域。这些方法通常分为两大类:基于谱峰搜索的算法 [4] [5] [6] 和基于求根的算法 [7] [8] [9] [10] 。基于谱峰搜索的算法需要在雷达一定的角度范围内进行角度搜索,所以其估计精度和计算量与搜索步长紧密相关,且两者相互矛盾。如果步长选择比较大,该类算法的计算量比较小,但测角精度不高;反之,步长选择较小可在一定程度上提高精度,但计算量会急剧增加。与基于谱峰搜索的算法相比,基于求根的算法表现出更高的角度分辨率和更低的计算量。迄今为止,各国学者已经提出了很多基于求根的算法,如求根MUSIC算法(RM, Root MUSIC) [7] 和求根最小模算法(RMN, Root Minimum Norm) [8] ,但这些方法都需要进行高阶多项式求根,而高阶多项式求根可能得到多余的根,导致DOA估计出现错误。为了解决这个问题,文献 [9] 中提出了一种基于噪声子空间的快速求根MUSIC算法;文献 [10] 中,提出了新的基于二阶和四阶(FO, Fourth Order)统计的简化多项式求根算法,但是高阶统计量同样会带来计算量较大的问题。
本文提出了一种新的基于信号子空间的多项式求根算法。利用子空间理论,我们推导了所提算法的M阶多项式的系数,并给出了具体的多项式计算公式,然后通过计算一个M阶多项式的根可以获得M个DOA。与其他多项式求根算法相比,所提算法实现简单,更适合于大型阵列。
2. 算法描述
2.1. 信号模型
考虑一个有L个阵元且阵元间间距为半波长的均匀线性阵列,从
方向接收M个窄带平面波信号。假设信号和噪声是平稳、零均值的不相关过程,噪声是均值为零的白噪声,方差为
。阵列接收的回波信号模型为
(1)
式中,
是接收的数据向量,
是信号向量,
是噪声向量,
是导向矢量矩阵,
,
;N是快拍数。
阵列协方差矩阵为
(2)
式中,H表示埃尔米特转置。
通过对R进行特征分解,可以得到
维的信号子空间矩阵
,它由协方差矩阵R的M个最大特征值对应的M个特征向量组成。
2.2. 算法原理
因为
的秩是M,假设存在一个
维的向量
和一个
向量
满足
(3)
定义
(4)
式中,
是一个M×M的子矩阵,
是一个
的子矩阵,把式(4)带入式(3)中,
可以表示为
(5)
式中,
表示矩阵
的逆。
令
,那么转向矢量可以写成
(6)
由于信号子空间与入射信号的导向矢量所组成的空间相同,根据式(3),可定义如下的多项式
(7)
现在
已经由式(6)确定,多项式G(z)为
(8)
式(8)具有M个根,其对应于M个信号的DOA。在计算得到式(8)的M个根
之后,信号的DOA可表示为
(9)
式中,
表示取
的相位。
2.3. 算法步骤
由上述分析,该算法基本步骤可归纳如下:
(1) 由阵列接收的数据X(n)估计阵列协方差矩阵
;
(2) 对协方差矩阵进行提特征值分解或奇异值分解,得到信号子空间Us;
(3) 将信号子空间Us分为M × M和
两个子矩阵
和
,并利用式(5)计算得到多项式系数c;
(4) 根据式(8)构造多项式,求出多项式的M个根,并利用式(9)计算得到各信号的DOA。
3. 计算量分析
表1给出了所提算法、RM、RMN和文献 [9] 中多项式求根算法的计算量对比。

Table 1. The computational cost of polynomial rooting for four methods
表1. 四种算法多项式求根的计算量
从表1中我们知道,所提算法的多项式求根的计算量与L无关,对于大型阵列,其阵元数远远大于目标数,即
时,所提算法计算量要远远小于RM、RMN和文献 [9] 中的算法。因此,本文所提的算法更适用于大型阵列的DOA估计。

Figure 1. Computational cost of the polynomial rooting for four methods versus L
图1. 四种算法多项式求根的计算量随L变化曲线
图1给出了四种方法的多项式求根计算量随L的变化曲线。仿真过程中,假设信源数M = 2,阵元数L在5到100之间按步长5变化。从图中可以看出:所提算法的计算量不随阵元数变化,且当
时,另外三种多项式求根算法的计算量几乎相同,要远远大于本文所提算法。
4. 计算机仿真结果
仿真过程中,假设均匀线阵阵元数L = 10,快拍数N = 256。
图2给出了信噪比SNR = 15 dB时,RM算法、RMN算法和所提算法对位于60˚方向信号的DOA估计结果。从图中可以看出,RM算法需要计算2L − 2 = 18个根,正确根位于单位圆附近且成对出现;RMN算法需计算L − 1 = 9个根,正确根位于单位圆附近;而本文所提算法只需计算M = 1个根,可以较为精确地估计出目标的DOA,且不会出现多余错误的DOA估计值。
 (a)
(a) 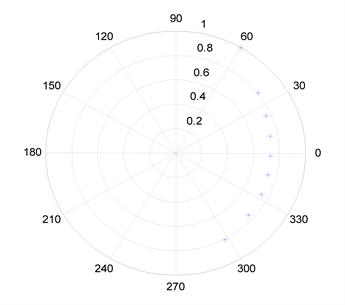 (b)
(b)  (c)
(c)
Figure 2. DOA estimated results with SNR = 15 dB of three algorithms for the one signal. (a) RM algorithm; (b) RMN algorithm; (c) The proposed algorithm
图2. SNR = 15 dB时,三种算法对单个信号的DOA估计结果。(a) RM算法;(b) RMN算法;(c) 所提算法
 (a)
(a)  (b)
(b) 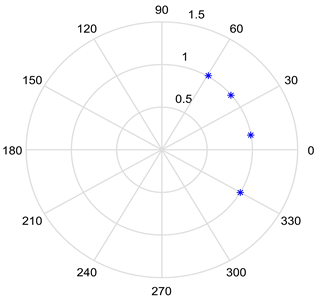 (c)
(c)
Figure 3. DOA estimated results with SNR = 20 dB of three algorithms for the one signal. (a) RM algorithm; (b) RMN algorithm; (c) The proposed algorithm
图3. SNR = 20 dB时,三种算法对单个信号的DOA估计结果。(a) RM算法;(b) RMN算法;(c) 所提算法
图3给出了信噪比SNR = 20 dB时,RM算法、RMN算法和所提算法对位于−30˚、10˚、40˚、60˚四个方向信号的DOA估计结果。同样从图中可以看出:RM算法和RMN算法都会得到多余的根,而本文所提的算法有几个信号就计算多少个根,不会产生错误的DOA估计。因此,本文所提算法具有更高的计算效率。
图4则给出了估计的均方根误差RMSE随SNR的变化曲线,仿真曲线为500次蒙特卡罗实验统计结果。从图3可以看出:各种算法的DOA估计的均方根误差大小为RMSE (RM算法) < RMSE (RMN算法) < RMSE (所提算法) ≈ RMSE (文献 [9] 算法) < RMSE (文献 [10] 算法)。但是,总体来看,上述五种算法在信噪比较大时,都具有较好的DOA估计性能。
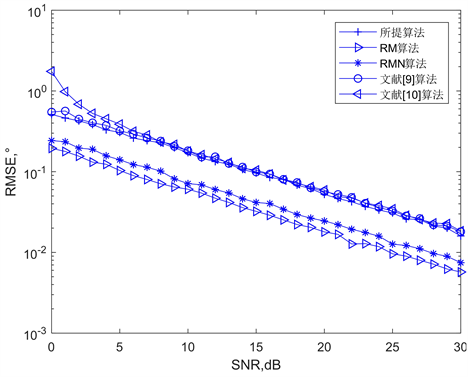
Figure 4. MSEs against SNR from 500 Monte Carlo simulations
图4. 500次蒙特卡罗仿真随信噪比变化曲线
5. 结论
为了降低多项式求根类算法的计算量,本文提出了一种基于信号子空间的多项式求根算法。该算法不产生无关根,且其所有多项式根都对应于所估计信号的DOA。通过算法计算量分析,可以看出:所提算法的计算量与阵元数无关,相比现有的多项式求根类算法,该算法更适用于大型阵列的DOA估计。计算机仿真结果表明:所提算法能够较为精确地估计出信号的DOA,且具有较好的角度估计性能。
基金项目
本文工作获得陕西省自然科学基础研究计划项目(2023-JC-YB-553, 2023-JC-YB-491)资助。
NOTES
*通讯作者。