维吾尔族馕中蕴含的几何元素及在数学课堂教学中的应用

The Geometric Elements Contained in Uygur Naan and Their Application in Mathematics Teaching

摘要: 馕作为新疆维吾尔族的特色饮食，其中蕴含了很多几何元素；馕的图案主要由圆构成，还包含大量通过旋转和平移得到的美丽花纹，馕坑的设计又与抛物线相关。本文以馕创设数学教学情境，分析其中的数学知识，能够很好地调动新疆地区学生学习兴趣，提升新疆地区数学教育水平。

Abstract: Naan is the characteristic diet of Xinjiang Uygur nationality, which contains a lot of geometric elements. The pattern of Naan consists mainly of circles, and also contains a large number of beautiful patterns obtained by rotation and translation. The design of the Naan pit is also related to the parabola. This paper, by creating mathematics teaching situation with Naan, analyses the mathematical knowledge, which can mobilize the interest of students, and raise the level of mathematics edu-cation in Xinjiang.

1. 引言

馕，是维吾尔族的传统饮食，距今已有上千年的历史。无论是日常饮食还是重大节日，维吾尔族人民的餐桌上总少不了馕的身影，馕已经融入维吾尔族文化中。馕为什么在维吾尔族饮食长期占据重要地位呢？是由于维吾尔族人民长期居住在新疆这样气候干燥，绿色植被较少的地区，缺乏树木植物作为燃料，馕在馕坑中烤制不仅节省燃料，还能长期储存，并且食用时能与新疆特色水果干果搭配食用。馕很好地与维吾尔族生活方式和生态环境相适应，从而成为维吾尔族人民最喜爱的食物，“宁可三日无肉，不可一日无馕”这句谚语充分体现了馕在维吾尔族人民心中崇高的地位。

馕在烤制的过程中，为了防止馕在烤制过程中面膨胀，维吾尔族人民会用馕戳在馕胚表面戳出花纹，使得烤出的馕有了美观的图案 [1] 。随着维吾尔族人民的不断创新，又研制出了有着丰富的种类和形状的馕。在这些馕中，蕴含了很多几何元素。

2. 主要内容

2.1. 馕中的圆

维吾尔族馕基本形状都是圆，馕的外轮廓是圆，馕边是圆环，馕中戳出的花纹也是圆。为什么维吾尔族会在馕中运用如此多与圆有关的几何元素？一方面将馕做成圆的，体积小，运输方便，尤其是古代商人在丝绸之路上行走时，圆形的馕是他们最易携带的干粮；另一方面，圆意味着团圆，与维吾尔族人民热情好客，喜爱聚会的性格特点相吻合，大家把圆馕进行分食，寓意着将团圆幸福带给每一个人。

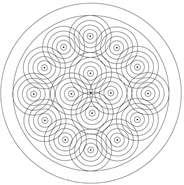
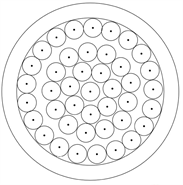
(a) (b) (c) (d)

Figure 1. Schematic diagram of Naan

图1. 馕的示意图

不同种类的馕，其中的圆的形式也不相同。图1(a)的馕，里面的花纹是一个个小圆组成，其几何图形如图1(b)所示，从内圈到外圈分别由1、7、13、21个半径相同的小圆相切组成。而图1(c)中的馕，里面的花纹是由大小不一的同心圆组成，其几何图形如图1(d)所示，内圈由4组同心圆组成，外圈由12组同心圆组成，每组同心圆都由5个间距相等的小圆组成。

馕中的这些圆，能够很好地帮助学生学习有关于圆与圆的位置关系，在课堂教学中能够提出以下问题：

1) 在图1(b)中哪些圆是外切关系？哪些圆是内切关系？哪些圆是外离关系，哪些圆是内含关系？

2) 在图1(b)中最外圈的小圆为等圆，半径为r，且这21个等圆中任意一个等圆都与相邻的等圆外切，则与这21个等圆内切的大圆半径R是多少？

3) 在图1(d)中如何通过小圆之间圆心距和半径的关系来判断小圆之间的外离、外切、相交关系？

将这些问题在课堂中提出，能够让学生感受到生活中处处有数学，从而很好地激发新疆地区学生的学习兴趣。

2.2. 馕中的旋转和平移

维吾尔族在制作馕时，会将馕胚放在一块圆形的底座上进行抹油、印花纹等操作，做的过程中不断旋转底座，因而制作出的馕的图案几乎都由一个图形旋转而来。如图2(a)~(f)中的馕，它们的形状，其中的花纹都是旋转而成。

(a) (b) (c)(d) (e) (f)

Figure 2. Pattern rotation in Naan

图2. 馕中的图案旋转

馕中的图案不仅由旋转而成，还有通过平移构成的。如图3(a)中的馕，它的图案是由一个波浪图案平移得到，图3(b)中的馕，它的图案可以看做是由一个菱形平移得到，也可以看做是由三个相邻的菱形上下平移得到。

(a) (b)

Figure 3. Pattern translation in naan

图3. 馕中的图案平移

旋转和平移不仅体现在馕中的图案，还体现在维吾尔族人民生活的方方面面，他们的服饰、建筑、日常用品，都包含通过旋转和平移而形成的图案。新疆地区的教师在进行图形与几何课堂设计的时候，就可以将这些来源于生活中的素材运用进去，从中抽象出数学知识，从而启发学生思考，更好地培养学生的直观想象能力和数学抽象思维 [2] 。

2.3. 馕坑中的抛物线和抛物面

烤出来的馕表面金黄，味道独特，与它的烤制方式有着很大的关系，馕坑就是维吾尔族人民几千年的智慧成果。如图4所示，在O点放置热能源(煤炭或木炭)，发出的热辐射大部分能被馕坑侧边多次反射，从而实现对热能的充分利用并在短时间内就将馕烤熟。而这样特别的设计与抛物线的光学性质有关，如图5所示，馕坑主体横截面是由图5(b)所示的两个抛物线组成，O点是两个抛物线的共同焦点 [3] 。两条抛物线绕中心轴旋转后会形成两个抛物面，组合后用上下两个平面截割就是馕坑的结构，更进一步地，可以用定积分算出馕坑内侧的表面积和容积。因此，不仅是馕的图案，馕坑中也含有关于几何的数学知识。

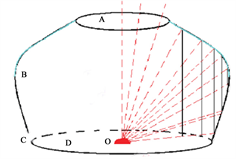
Figure 4. Schematic diagram of the Naan pit

图4. 馕坑示意图

Figure 5. Cross section of the main body of the Naan pit

图5. 馕坑主体横截面

(图片来源：阿布都艾则孜·阿布来提，艾力·如苏力，博尔汗·沙来，等《维吾尔族馕坑几何结构及新能源馕坑的设计》 [3] )

由此，可以根据馕坑的横截面建立直角坐标系，在课堂教学中提出关于抛物线的问题：

1) 已知两抛物线与上下两条直线的交点和公共焦点F，求出抛物线的曲线方程。

2) 已知两条抛物线的曲线方程，求出两条抛物线的交点坐标。

通过学生熟悉的生活实例，从中抽象出圆锥曲线，从而营造出贴合新疆民族文化的数学学习氛围，让学生能够更有热情地学习复杂的圆锥曲线，理解焦点名称的由来，培养学生的数学核心素养。

2.4. 以馕创设的数学情境化教学案例

当前的数学教科书中的素材和课堂教学中的情景与少数民族地区学生的生活环境有一定的脱节，再加上高度抽象化的数学语言和复杂的公式，使得少数民族学生会感到数学是枯燥难学的 [2] 。而如果能将具体的民族数学实例整合到课堂教学中，就能够让学生感受到数学并不是脱离生活的 [4] 。因此结合维吾尔族生活实际，改变数学内容的呈现方式，在数学世界与现实世界之间搭建桥梁，开发基于民族数学的情境化教学案例，能更容易让新疆地区学生理解数学知识，提升对数学的兴趣 [5] 。馕作为维吾尔族学生熟悉的饮食，能从中创设出以下数学情境化教学案例。

案例1：图6是新疆特产牛乳馕，酥香可口，奶香浓郁，图7是它的几何图形，以O点为圆心，有3个同心圆，从小到大分别命名为 $O_1$ ， $O_2$ ， $O_3$ ，半径分别为 $r_1$ ， $r_2$ ， $r_3$ ；现在要把这个馕分给两个人吃，于是把馕切了一刀，用直线表示，与最大的圆 $O_1$ 相交于点 $A$ ， $B$ ，圆心角 $\angle AOB$ 为 $\theta$ ，基于此情境，提出以下数学问题：

1) 直线 $AB$ 与3个圆分别有什么位置关系？

2) 求出弧 $AB$ 的长度，弦 $AB$ 的长度，三角形 $AOB$ 的面积。

3) 设 $OA$ ， $OB$ 与圆 $O_2$ 的交点为 $C$ ， $D$ ，与圆 $O_3$ 的交点为 $E$ ， $F$ ，求扇形 $AOB$ ，扇形 $COD$ 和扇形 $EOF$ 的面积，并求出面积比，说出面积比与半径比的关系。

Figure 6. Schematic diagram of milk naan

图6. 牛乳馕示意图

在这个案例中创设了一个切馕的情境，从中抽象出直线和圆，引发数学思考，联想到直线与圆的位置关系，扇形面积等内容，让学生体会到数学知识之间的联系性，培养学生的数学思维和抽象能力。

案例2：馕摊上为了更好地利用空间，会将馕整齐排列，摞在一起，如图8所示，从上到下每层馕的数量分别为1，2，3，4，5，6，构成了一个等差数列；而图9展示了另外一种馕的排列方式，每层可以看作一个三角形，从第二层到第6层的三角形的边分别需要2，3，4，5，6个馕排列而成，基于此情境，提出以下数学问题：

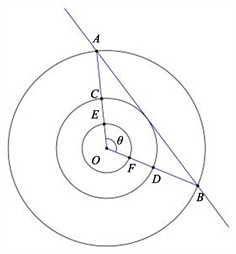
Figure 7. Schematic diagram of the geometric shape of milk naan

图7. 牛乳馕几何图形示意图

Figure 8. Naan arrangement diagram 1

图8. 馕排列示意图1

Figure 9. Naan arrangement diagram 2

图9. 馕排列示意图2

1) 写出两个数列的通项公式。

2) 有两位顾客分别要买下两个摊位上所有的馕，两个人分别买了多少个馕？如果摞了n层馕，那么两个人分别买了多少个馕？

在这个案例中，将图片中馕的排列方式，用数列来进行表示，体现了数形结合的思想，并创设买馕的情境，将求数列前n项和的内容融入其中，让学生感受到数学在日常生活中的作用，从而激发学生学习数学的热情。

3. 结束语

数学课程标准(2022年版)提出要围绕教学任务，选择贴近学生生活经验和认知加工特点的素材进行真实情景的创设 [6] 。对于新疆维吾尔族学生来说，馕无疑是他们日常生活中再熟悉不过的食物，探究馕中的几何元素，将馕运用到图形相关的教学中，符合数学课程标准的要求，从而帮助学生了解民族中特有的数学智慧，感受到数学在生活中无处不在，提升数学学习兴趣，这对于提升新疆地区的数学教育来说有着重要作用。

基金项目

国家自然科学基金项目(NO. 12361072)；2022新疆师范大学校级教学团队项目；2021新疆师范大学校级一流课程项目。

NOTES

^*通讯作者。