基于灰色模糊理论的“虚拟养老院”老人满意度评价研究

Research on the Satisfaction Evaluation of the Elderly in “Virtual Nursing Home” Based on Grey Fuzzy Theory

摘要: 本文以兰州市城关区“虚拟养老院”为例，对223位老人进行满意度问卷调查，从资源、服务和费用三个方面入手，将其作为一级指标对“虚拟养老院”的满意度进行综合评价，其组成的评价指标体系包括工作人员数量、工作人员服务态度和生活服务费用等15个二级指标。采用灰色关联分析法计算权重，模糊综合评价法得出评价矩阵进而得到最终结果，研究结果显示老人满意度为一般满意，其中对费用方面最为满意。

Abstract: Taking the “Virtual Nursing Home” in Chengguan District, Lanzhou City as an example, this paper conducts a satisfaction questionnaire survey on 223 elderly people. Starting from the three aspects of resources, services and costs, it is used as a first-level indicator to comprehensively evaluate the satisfaction of the “Virtual Nursing Home”. The evaluation index system consists of 15 secondary in-dicators such as the number of staff, staff service attitude and living service cost. The grey correla-tion analysis method is used to calculate the weights, and the fuzzy comprehensive evaluation method is used to obtain the evaluation matrix and then obtain the final result. The research re-sults show that the satisfaction of the elderly is generally satisfactory, and the most satisfied with the cost.

1. 引言

目前养老问题日趋严峻，2020年第七次人口普查显示人口年均增长率越来越低，60岁及以上人口为2.54亿，占总人口的18.7%，较去年同比增长3.99% [1] 。现在的养老方式大多都是子女养老或者机构养老，但是一方面现在的家庭模式基本上是“4 + 2 + 1”，子女在外工作以致存在许多空巢老人；另一方面机构价格高，床位少，服务单一，更甚者存在虐待老人现象，都能体现当今传统养老模式已不再能引领主流。而近年来“虚拟养老院”因为服务多样，投入成本低等优势使智慧居家养老成为可能，为老年人所喜爱 [2] 。但虚拟养老院仍存在着评价机制不完善，宣传力度不够和专业化程度不高 [3] 等问题，为了保证服务质量，本文对“虚拟养老院”进行满意度评估。

一直以来，满意度都被当作是衡量和检验质量的重要指标。陆伟峰等 [4] 利用SD关键变量入树建模法提出了社区嵌入式养老项目利益相关方满意度动态均衡管理策略，为养老满意度动态模拟和评价做铺垫；赵秀秀等 [5] 使用灰色关联分析得出隶属矩阵并结合AHP得到各指标的权重研究物业满意度，减少了主观因素的影响；刘莎等 [6] 结合灰色关联分析法和多层次模糊综合评价法进行病人满意度评价，使测评分析结果更加客观真实；Barik Kousik等 [7] 提出了一种基于区块链的多维朴素贝叶斯-K近邻和多目标Logistic粒子群优化算法相结合的消费者满意度预测方法，对服务和质量做出更好的决策；孙中艮等 [8] 使用ACSI模型探讨期望质量、感知质量、感知价值、社会支持、满意度及忠诚度之间的关系，避免了单一指标使评价结果不精确的问题；Abiyev Rahib H.等 [9] 提出了二型模糊集与联合分析相结合的方法，利用顾客对视觉、声音、味觉、触觉和嗅觉等感官变量的意见来评价顾客满意度，提高了测评满意度的有效性；郭炜等 [10] 构建了基于灰色模糊理论的综合评价模型，结果表明该模型准确、合理且具有一定的有效性与实用性；贾玉虎等 [11] 采用灰色关联方法和灰色聚类方法，构建顾客满意度测评信息系统，使测评结果更加趋于真实；Si Amalendu等 [12] 基于登普斯特-Shafer证据理论和灰色关联分析的图片模糊集决策方法使其在COVID-19药物选择中得到更优解及应用；Hashemkhani Zolfani Sarfaraz等 [13] 通过灰色关联分析以及2型中智模糊集(T2NFN)为海运公司对集装箱船进行选择，提高其海运效率。

2. 基于灰色模糊理论的满意度评价模型

1965年L.A.Zadeh教授首次提出模糊理论，用模糊的观念来描述现实生活中的事情性质等级[6]。然而对于满意度评价这种多指标问题，权重系数的分配对结果有很大影响，因此怎样才能使得权重更加合理就成为了模糊理论中研究的重点课题。相较于用专家法来确定权重，不仅在专家少的情况下有一定不准确性，而且对于事物的不确定性也因为专家的个人差异而得到不准确的结果，但是满意度又是一个模糊的概念难以用确定性的集合来描述，它具有随机性、不完备性、不确定性以及模糊性，即具有灰色性。1982年邓聚龙教授提出的灰色系统理论可以根据少量样本、部分信息把不确定性问题得到有效解决，灰色聚类法是灰色系统分析中一种应用广泛的方法。考虑“虚拟养老院”的数据情况，本文采用灰色聚类法中的灰色关联聚类计算权重并且利用灰色白化权聚类 [14] 改进模糊综合评价中的隶属矩阵，形成灰色模糊综合评价 [15] 。满意度评价模型从计算步骤上分为指标权重的确立和评价矩阵的生成。

2.1. 基于灰色关联度的权重系数

本文通过向城关区“虚拟养老院”的老人发放223份调查问卷，问卷中分值为百分制，含义为：[0~60)表示非常不满意，[60~70)表示比较不满意，[70~80)表示一般满意，[80~90)表示比较满意，[90~100]表示非常满意，问卷中的题项包含3个一级指标和15个二级指标，如图1。

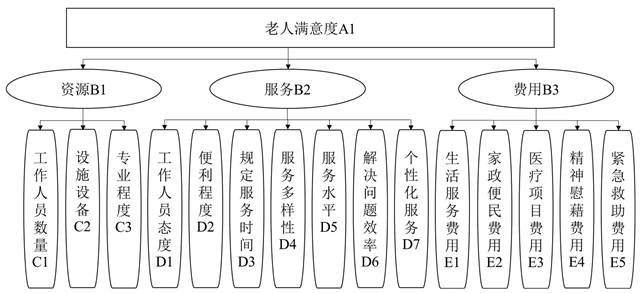
Figure 1. Evaluation index system diagram

图1. 评价指标体系图

请专家进行打分，如表1所示。

Table 1. Expert weight assignment table

表1. 专家权重赋值表

为了避免出现个别数值上的偏差而影响结果的准确性，在请专家打分后对分值进行相似度检验 [15] ：

$R_{ab}=1-{\left(\frac{1}{m}{\displaystyle \underset{j=1}{\overset{m}{\sum }}{\left(w_{aj}-w_{bj}\right)}^2}\right)}^{1/2}$

其中， $w_{aj}$ 表示a专家对j指标的权重赋值， $w_{bj}$ 表示b专家对j指标的权重赋值，m表示指标总数， $R_{ab}$ 表示a专家的权重赋值对b专家的偏离情况的相似程度。

$X_a={\displaystyle \underset{i=1}{\overset{k}{\sum }}{R}_{ai}}$

其中， $X_a$ 表示a专家的权重赋值的总偏离程度。

$X={\left(X_1,X_2,\cdots ,X_k\right)}^{\text{T}}$

$P_a=\frac{X_{\max }-X_a}{X_{\max }}\times 100\%$

计算完成后得到偏离矩阵，当最大偏离系数值小于0.5%时，认为数据有效。

其中， $X_{\max }$ 表示总偏离程度最大值， $P_a$ 表示a专家的偏离系数。

计算得到偏离系数分别为0.09%，0.22%，0.16%，0.03%，0.19%，0.11%，0.05%，皆小于0.5%于是数据全部保留。

计算灰色关联系数，如下式，其中取 $\rho =0.5$ 。

${\xi }_i\left(j\right)=\frac{\underset{i}{\min }\underset{j}{\min }|y\left(j\right)-x_i\left(j\right)|+\underset{i}{\max }\underset{j}{\max }|y\left(j\right)-x_i\left(j\right)|}{|y\left(j\right)-x_i\left(j\right)|+\rho \underset{i}{\max }\underset{j}{\max }|y\left(j\right)-x_i\left(j\right)|}$

通过对关联系数求平均值得到关联度，结果如表2所示。

Table 2. Grey correlation coefficient and correlation degree

表2. 灰色关联系数及关联度

2.2. 灰色模糊评价模型确立

评价对象的因素集为 $U=\left\{U_1,U_2,U_3\right\}=$ {资源，服务，费用}，

每个子集的具体分类为：

$U_1=\left\{U_{11},U_{12},U_{13}\right\}=$ {工作人员数量，设施设备，专业程度}；

$U_2=\left\{U_{21},U_{22},U_{23},U_{24},U_{25},U_{26},U_{27}\right\}=$ {工作人员态度，便利程度，规定服务时间，服务多样性，服务水平，解决问题效率，个性化服务}；

$U_3=\left\{U_{31},U_{32},U_{33},U_{34},U_{35}\right\}=$ {生活服务费用，家政便民费用，医疗项目费用，精神慰藉费用，紧急救助费用}。

评语集 $V=\left\{V_1,V_2,V_3,V_4,V_5\right\}=$ {非常满意，比较满意，一般满意，比较不满意，非常不满意} = {100, 90, 80, 70, 60}。

对求得的关联度进行归一化处理，得到最终权重见表3，权重集如公式所示。

$W_j={\left(w_1,w_2,\cdots ,w_n\right)}^{\text{T}},{\displaystyle \underset{i=1}{\overset{n}{\sum }}{w}_i}=1$

Table 3. Weight of satisfaction evaluation indicators

表3. 满意度评价指标的权重

用c = 5，4，3，2，1表示评价灰类，取区间中点为中心点，同时左右各延拓半个区间长度。

第一灰类“非常满意”(c = 1)，其白化权函数为：

$f_i^1\left(x\right)=\{\begin{array}{cc}0& x\notin \left[85,105\right]\\ 1& x\in \left[95,105\right]\\ \frac{x-85}{10}& x\in \left[85,95\right]\end{array}$

第二灰类“比较满意”(c = 2)，其白化权函数为：

$f_i^2\left(x\right)=\{\begin{array}{cc}0& x\notin \left[75,95\right]\\ \frac{95-x}{10}& x\in \left[85,95\right]\\ \frac{x-75}{10}& x\in \left[75,85\right]\end{array}$

第三灰类“一般满意”(c = 3)，其白化权函数为：

$f_i^3\left(x\right)=\{\begin{array}{cc}0& x\notin \left[65,85\right]\\ \frac{85-x}{10}& x\in \left[75,85\right]\\ \frac{x-65}{10}& x\in \left[65,75\right]\end{array}$

第四灰类“比较不满意”(c = 4)，其白化权函数为：

$f_i^4\left(x\right)=\{\begin{array}{cc}0& x\notin \left[30,75\right]\\ \frac{75-x}{10}& x\in \left[65,75\right]\\ \frac{x-30}{35}& x\in \left[30,65\right]\end{array}$

第五灰类“非常不满意”(c = 5)，其白化权函数为：

$f_i^5\left(x\right)=\{\begin{array}{cc}0& x\notin \left[-30,65\right]\\ \frac{65-x}{35}& x\in \left[30,65\right]\\ 1& x\in \left[-30,30\right]\end{array}$

计算隶属矩阵公式：

${\epsilon }_{ijc}={\displaystyle \underset{i=1}{\overset{k}{\sum }}{f}_{ij}^c(\; x\; )}$

$S_{ijc}=\frac{{\epsilon }_{ijc}}{{\epsilon }_{ij}}$

${\epsilon }_{ij}={\epsilon }_{ij1}+{\epsilon }_{ij2}+{\epsilon }_{ij3}+{\epsilon }_{ij4}+{\epsilon }_{ij5}$

$S=\left(\begin{array}{c}{S}_{i1}\\ S_{i2}\\ ⋮\\ S_{ij}\end{array}\right)=\left(\begin{array}{cccc}{S}_{i11}& S_{i12}& \cdots & S_{i15}\\ S_{i21}& S_{i22}& \cdots & S_{i25}\\ ⋮& ⋮& \ddots & ⋮\\ S_{ij1}& S_{ij2}& \cdots & S_{ij5}\end{array}\right)\left(i=1,2,\cdots ,5\right)$

其中， ${\epsilon }_{ijc}$ 为灰色评价系数， $S_{ijc}$ 为隶属度， $S_{ij}$ 为隶属向量， $S$ 为隶属矩阵。

求得结果如表4所示。

计算模糊综合评价矩阵公式：

$\begin{array}{c}{Z}_i=W_i\cdot S_i\\ =\left(w_{i1},w_{i2},\dots ,w_{i{l}_i}\right)\left(\begin{array}{cccc}{S}_{i11}& S_{i12}& \cdots & S_{i1k}\\ S_{i21}& S_{i22}& \cdots & S_{i2k}\\ ⋮& ⋮& \ddots & ⋮\\ S_{i{l}_{i}1}& S_{i{l}_{i}2}& \cdots & S_{i{l}_{i}k}\end{array}\right)\\ =\left(z_{i1},z_{i2},\dots ,z_{ik}\right)\left(i=1,2,\cdots ,m\right)\end{array}$

对 $Z_i$ 进行归一化处理；

$Z_i=\frac{Z_{ij}}{{\displaystyle \underset{j=1}{\overset{5}{\sum }}{Z}_{ij}}}\left(i=1,2,3,4,5\right)$

求得结果分别为：

$Z_{B1}=\left(0.00830.04030.33260.36280.256\right)$ ;

$Z_{B2}=\left(0.0030.0310.29140.5350.1396\right)$ ;

$Z_{B3}=\left(0.0080.13240.43840.30920.112\right)$ .

Table 4. Evaluation of grey class values and membership matrices

表4. 评价灰类数值及隶属矩阵

最终得分为：

$F_{B1}=Z_{B1}\cdot V^{\text{T}}=\left(0.00830.04030.33260.36280.256\right){\left[10090807060\right]}^{\text{T}}=71.821$ ;

$F_{B2}=Z_{B2}\cdot V^{\text{T}}=\left(0.0030.0310.29140.5350.1396\right){\left[10090807060\right]}^{\text{T}}=72.228$ ;

$F_{B3}=Z_{B3}\cdot V^{\text{T}}=\left(0.0080.13240.43840.30920.112\right){\left[10090807060\right]}^{\text{T}}=76.152$ .

因此，结果表明老人对城关区“虚拟养老院”属于一般满意的等级。

3. 结语

对于老龄化现状，“虚拟养老院”在老年人的智慧便利生活上起到一个导向作用。作为服务行业，满意度是衡量该行业是否成功的重要指标，本文在前人的理论以及研究上使用灰色系统理论模型，用灰色关联法确定权重，可以解决专家赋权小，样本信息难处理的问题，而且在隶属矩阵的确定上使用白化权函数，克服了单一方法的不足，使得评判结果更加真实可靠。

本模型可以对满意度进行更加全面的评价，使满意度评判的可信度有一定提高，一方面，可以帮助“虚拟养老院”及时收到老人的反馈而做出调整，提高老人的满意度；另一方面，建立了一套较为全面的评价机制，可以起到内部督促的作用。此外，该模型还可以应用于其它“虚拟养老院”的满意度评价或者其它服务行业测评标准的研究，有一定的扩展性。

基金项目

湖南省研究性创新创业计划项目资助(编号S202310553030)。