基于改进粒子群优化算法的光纤传感网络的布置优化

Layout Optimization of Optical Fiber Sensor Network Based on Improved Particle Swarm Optimization Algorithm

摘要: 光纤光栅传感网络的有效性在很大程度上取决于传感器部署方案所提供的覆盖范围。为了提高光纤光栅传感网络的覆盖率，需要对传感器的布置进行优化。本文提出一种基于改进粒子群算法的光纤传感网络的布置优化，通过余弦自适应调整惯性权重，同时利用惯性权重来调整学习因子，提高了算法的收敛精度。并基于传统传感器的检测区域模型，建立了更加贴合光纤光栅传感器特点的检测区域模型。以光纤光栅传感器网络覆盖率为目标函数，使用改进粒子群算法对传感器布置进行优化研究。仿真实验结果表明，在传感器节点数为25时，与PSO、UPSO、IABC三种智能优化算法相比，改进后的粒子群算法对目标区域的覆盖提升率分别提高了5.54%、3.81%、4.73%，在解决传感器节点覆盖优化问题方面表现出了显著的优越性。

Abstract: The effectiveness of FBG sensor networks depends heavily on the coverage provided by sensor de-ployment scenarios. In order to improve the coverage of FBG sensor networks, the sensor placement needs to be optimized. In this paper, a layout optimization of optical fiber sensor network based on improved particle swarm algorithm is proposed, which adjusts the inertia weight by cosine adapta-tion, and uses the inertia weight to adjust the learning factor, which improves the convergence ac-curacy of the algorithm. Based on the detection area model of the traditional sensor, a detection ar-ea model that is more in line with the characteristics of FBG sensors is established. Taking the FBG sensor network coverage as the objective function, the improved particle swarm algorithm is used to optimize the sensor layout. The experimental results show that compared with the three intelli-gent optimization algorithms of PSO, UPSO and IABC, the coverage improvement rate of the im-proved particle swarm algorithm on the target area is increased by 5.54%, 3.81% and 4.73%, re-spectively, when the number of sensor nodes is 25, which shows significant superiority in solving the problem of sensor node coverage optimization.

1. 引言

随着技术的不断进步，传感器在大型结构和设备的健康监测中得到了广泛应用，例如铁路沉降、管道泄漏和机翼损坏等 [1] [2] [3] 。然而，传统传感器往往容易受到电磁干扰的影响，且耐腐蚀性能较差，难以满足长期监测的安全要求。此外，由于传感器数量众多，其重量不容忽视。相比之下，光纤布拉格光栅(Fiber Bragg Grating, FBG，以下简称光纤光栅)传感器具有灵敏度高、体积小、重量轻、成本低、抗电磁干扰、耐腐蚀性能好等优点。光纤光栅传感器不仅集信号传感和传输于一体，且不会影响结构的完整性 [4] [5] [6] [7] 。基于以上这些优点，光纤光栅传感器可以很好的应用在结构健康监测(Structure Health Monitoring, SHM)中。为了全面掌握大型结构的健康状况，需要同时对结构进行多点的监测，光纤光栅具有分布式测量的能力，易于形成波分复用和时分复用的拓扑结构监测阵列，从而实现环境参数的分布式实时在线监测。

Randhir Kumar Sah和Amitesh Kumar等人 [8] 利用FBG传感器进行土木结构的裂纹监测，将波长映射到时间延迟的询问技术来观察光纤光栅传感器上产生的应变，最大限度地减少结构中错误裂纹检测的概率。ShoiOkagawa和Peter Bernus等人 [9] 利用FBG传感器获取健康数据并使用机器学习进行实时损伤分类的实时SHM系统。Shen和Shin等人 [10] 使用分布式光纤传感器，基于布里渊后向散射传感系统测量应变，准确检测管道中的缺陷。在实际监控过程中，传感器的数量会受到解调系统和光源波长带宽的影响，结构的特殊性也限制了传感器的数量。为了准确监测所有目标信息，需要合理部署传感器节点，同时尽可能减少成本和传感器数量。因此如何在有限的传感器数量下有效布置以提高测量精度、减少覆盖空洞、最大程度利用节点成为学者们研究的焦点。

随着近些年的发展，智能优化算法被广泛应用于传感器的布局优化，它们能够快速有效地搜索最优解，避免陷入局部最优。这些算法在传感器的布置优化上具有独特的优势，受到了许多学者的关注和研究 [11] [12] 。Shang等人 [13] 提出了一种基于粒子群算法(particle swarm optimization, PSO)的天线布局优化方法，可实现机载天线布局优化。该方法可以在保证最优效果的前提下提高最优速度，并通过偶极子天线验证了该方法的准确性。吴晓军等人 [14] 针对基本粒子群优化算法容易陷入局部最优解的问题，提出了一种均匀搜索粒子群算法(Uniform Particle Swarm Optimization, UPSO)，该算法可以很好的克服标准粒子群算法容易陷入局部最优的问题。张浩等人 [15] 提出了一种基于改进人工蜂群(Improve Artificial Bee Colony, IABC)的节点多目标部署优化策略，通过引入混沌初始化策略，仿真结果表明该算法能够有效提升节点的覆盖率。Huang和Zeng等人 [16] 针对标准人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)在光纤光栅传感器网络布局优化方面存在的缺陷，提出了三种自适应步长方法，提高了算法的收敛精度和速度。并且用实验结果表明，该算法具有较强的搜索性能，能使FBG传感器节点布局更加合理，适用于解决传感器布局优化问题。Liu和Ren [17] 采用改进的人工鱼群算法(Modified Artificial Fish Swarm Algorithm, MAFSA)建立FBG应变传感器网络优化模型，得到结构的应变值。与随机排列得到的应变值相比，减小了误差，提高了应变测量精度。

上述所提及的智能优化算法都存在着一定的不足，ABC算法收敛过程缓慢，容易出现未成熟收敛，难以达到预期的覆盖质量。AFSA算法计算复杂度高，特别是较大的问题空间中，并且由于算法的随机性，容易陷入局部最优。PSO算法全局搜索能力强、收敛速度快，但是容易陷入局部最优解。

基于以上分析，本文提出一种基于改进粒子群优化算法的光纤传感网络的布置优化，该方法可以有效提高FBG传感网络的覆盖率，实现FBG传感网络的布置优化。

2. 光纤光栅传感器的检测区域模型

传感器检测范围是传感器网络的基础因素，同时也是布置传感器节点的重要依据。目前，大多数研究都将传感器的检测范围简化为一个圆形，这种做法有利于处理和结构对称性，并且适用于大多数传感器。传统传感器的检测范围是以传感器为圆心、检测距离为半径的一个圆。传感器的检测很大程度上是由传感器的感知能力决定的。研究传感器的检测范围问题，需要了解传感器的感知模型与特性。感知模型有两大类，包括指数型和二进制感知型。为简化实验模型，本文定义在理想环境下，采用二进制感知型，即只有在圆形区域内，才能被检测到，且概率为1，圆形区域外则概率为0，该模型的描述如图1所示。假设目标与传感器的距离为D，传感器的检测半径为R，被检测的坐标位置为 $\left(x,y\right)$ ，设传感器的坐标位置为 $\left(m,n\right)$ 则目标与传感器的距离为D可以表示为：

$D=\sqrt{{\left(x-m\right)}^2+{\left(y-n\right)}^2}$ (1)

则被检测目标的覆盖情况为：

$P\left(x,y\right)=\{\begin{array}{cc}1& D\le R\\ 0& \text{otherwise}\end{array}$ (2)

由于光纤Bragg光栅传感器具有轴向敏感性，在不同方向上受到相等应力时，其波长漂移通常不同。因此，它的敏感范围可能呈椭圆形或其他形状，而不是标准的圆形。

FBG的波长漂移 $\Delta {\lambda }_{BS}$ 和它所受的轴向应变 $\Delta \epsilon$ 的关系式如式(3)所示：

$\Delta {\lambda }_{BS}={\lambda }_B\left(1-{\rho }_{\alpha }\right)\Delta \epsilon$ (3)

弹光系数 ${\rho }_{\alpha }$ 可以表示为：

${\rho }_{\alpha }=\left(\frac{n^2}{2}\right)\left[{\rho }_{\alpha }-v\left({\rho }_{11}-{\rho }_{12}\right)\right]$ (4)

式中：ν是泊松系数； ${\rho }_{11}$ 、 ${\rho }_{12}$ 是光纤光学应力张量分量 [18] 。可以看出传统传感器的感知模型不能完全适用于光纤光栅传感器，可以设定光纤光栅传感器的检测区域感知模型如图2所示。

Figure 1. Sensor detection area model based on perception model

图1. 基于感知模型的传感器检测区域模型

Figure 2. Detection area model of fiber grating sensor

图2. 基光纤光栅传感器的检测区域模型

在长半轴为a，短半轴为b的椭圆范围内各种因素限制程度较小，此时的传感器能有效地检测到应变信号。根据概率理论，可认为此时传感器能够完全覆盖此范围内信号源发出的信号，即覆盖率为1；当信号源位于长半轴为a，短半轴为b的椭圆范围以外时，信号损耗和噪声干扰等因素使传感器已经不能够有效地检测出信号，此时覆盖率为0。则被检测目标的覆盖情况为：

$P\left(x,y\right)=\{\begin{array}{cc}1& D\le 2a\\ 0& \text{otherwise}\end{array}$ (5)

其中，坐标 $\left(x,y\right)$ 表示被检测目标的位置，D用来表示一个被检测目标与一个传感器的距离。可设传感器的坐标位置为 $\left(m,n\right)$ ，则根据椭圆数学方程可知椭圆焦点 $c_1$ ， $c_2$ ：

$c=\sqrt{a^2-b^2}$ (6)

则距离D可以用以下方程式表示：

$D=\sqrt{{\left(m-c_1\right)}^2+n^2}+\sqrt{{\left(m-c_2\right)}^2+n^2}$ (7)

对于各项异性的材料，其在x方向和y方向的传播损耗是不同的，同时还需要考虑信号在传播过程中的各向异性特点。但在本文中，假定研究对象是各向同性的材料，因此不考虑传播损耗的影响。

设光纤传感网络中所有传感器检测概率为：

$P_j=1-{\displaystyle \underset{i=1}{\overset{N}{\prod }}\left(1-{P^{\prime }}_{ij}\right)}$ (8)

式中：N为光纤光栅传感器个数； $P_j$ 为信号源； ${P^{\prime }}_{ij}$ 表示对于第j个信号源，第i个光纤光栅传感器检测概率。光纤传感网络中，所有信号源被传感器检测到的概率均值表示为：

$P_A=\frac{\left({\displaystyle \underset{j=1}{\overset{M}{\sum }}{P}_j}\right)}{M}$ (9)

则未检测到的概率的平均值为：

$P_{AM}=1-P_A$ (10)

要得到传感器的最佳布局，要使得式(9)的值取值达到最大 [19] 即传感器的覆盖率。此即为传感器布局优化配置准则，通过此准则，调整传感器覆盖的密度，在被监测区域中重要区域部署更多的传感器节点，保证测量数据的准确性以及可靠性。

3. 改进粒子群算法

粒子群优化算法(Partical Swarm Optimization, PSO)是一种智能优化算法，它由Eberhart博士和Kennedy博士 [20] 于1995年提出。该算法灵感来源于对鸟群捕食行为的研究，其模拟了鸟群在寻找食物时的行为方式。粒子群优化算法以随机解为起点，通过迭代来寻找最优解，通过适应度函数来评价解的质量。

粒子群算法的基本原理：将搜索空间看作是一个n维空间，在其中定义一个由m个粒子组成的种群，每个粒子都是粒子群算法中的一个个体，且每个粒子的位置代表问题的一个可能解，第i个粒子的位置由n维向量表示，即 $x_i=\left(x_{i1},x_{i2},\cdots ,x_{in}\right)$ 。同时，每个粒子还有一个n维向量表示其在空间中的移动速度，即 $V_i=\left(v_{i1},v_{i2},\cdots ,v_{in}\right)$ 。粒子在搜索空间移动时包括了其历史上经过的最佳位置 $P_i=\left(p_{i1},p_{i2},\cdots ,p_{in}\right)$ 以及整个种群在空间中所找到的最佳位置 $P_g=\left(p_{g1},p_{g2},\cdots ,p_{gn}\right)$ 。通过跟踪这两个“极值”，PSO算法可以在空间中寻找到最优解。具体地，对于第i个粒子，它的速度和位置的更新公式如下：

$v_i\left(t+1\right)=w{v}_i\left(t\right)+c_1{r}_1\left(p_i\left(t\right)-x_i\left(t\right)\right)+c_2{r}_2\left(p_g\left(t\right)-x_i\left(t\right)\right)$ (11)

$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t+1\right)$ (12)

其中， $c_1$ 和 $c_2$ 为算法的两个学习因子，通常设置为1.5； $r_1$ 和 $r_2$ 为两个随机数； $p_i\left(t\right)$ 和 $p_g\left(t\right)$ 分别为粒子i在时间t的个体最优位置和整个群体的最优位置； $x_i\left(t\right)$ 和 $v_i\left(t\right)$ 分别为粒子i在时间t的位置和速度，w为算法的惯性权重，w可按如下公式变换：

$w\left(t\right)=0.1+0.9\cos \left(t/\text{maxgen}\right)$ (14)

通过余弦调整更新后的惯性权重，相比于固定的惯性权重粒子群的自适应性进一步增加，改进后的算法初期惯性权重较大，粒子的行为较为分散，搜索空间进一步增大，可以有效避免陷入局部最优，提高全局搜索能力；随着迭代次数的增加，惯性权重逐渐减小，粒子的行为集中，算法收敛速度加快。同时为了加强粒子学习能力，避免陷入局部最优，本文提出一种学习因子与惯性权重呈余弦函数关系的调整策略，更新后的学习因子公式为：

$\{\begin{array}{l}{c}_1\left(t\right)=c_{1s}+c_{1e}\cos \left(\pi w\left(t\right)\right)\hfill \\ c_2(t)=c_{2s}-c_{2e}\cos \left(\pi w\left(t\right)\right)\hfill \end{array}$ (15)

其中： $c_{1s}$ 和 $c_{1e}$ 分别为 $c1$ 的迭代初值和迭代终值， $c_{2s}$ 和 $c_{2e}$ 分别为 $c_2$ 的迭代初值和迭代终值。通过对Griewank、Sphere和Rosenbrock等典型测试函数的测试以及借鉴已有的学习因子调整策略，得到当 $c_{1s}=1.3$ 、 $c_{1e}=1.2$ 、 $c_{2s}=2$ 、 $c_{2e}=1.2$ 时，算法的效果最好。

通过以上分析改进后的粒子群算法公式为：

$v_i\left(t+1\right)=w\left(t\right)v_i\left(t\right)+c_1\left(t\right)r_1\left(t\right)\left[p_i\left(t\right)-x_i\left(t\right)\right]+c_2\left(t\right)r_2\left(t\right)\left[p_g\left(t\right)-x_i\left(t\right)\right]$ (16)

$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t+1\right)$ (17)

改进的粒子群算法流程图如图3所示：

Figure 3. Flow chart of improved particle swarm optimization algorithm

图3. 改进的粒子群算法流程图

4. 仿真实验结果分析

4.1. 实验模型建立

在应用改进粒子群算法布置优化实验之前，需要先建立一个传感器覆盖优化配置模型结构：一个由各向同性的材料构成的正方形板状结构，如图4所示。考虑到边界效应，不妨从一个无穷大的正方形板状结构中选取10 × 10的网格，并用121个黑色节点表示被检测目标的具体位置，放置若干个FBG传感器在10 × 10的网格区域中。其中每个传感器的覆盖半径为： $a=1.5$ 个网格单位； $b=1$ 个网格单位。

Figure 4. Sensor coverage optimization configuration model structure

图4. 传感器覆盖优化配置模型结构

4.2. 仿真实验内容

为了验证本文改进粒子群优化算法的性能，将改进粒子群算法分别与PSO、UPSO、IABC算法结果进行对比分析。为进行有效对比，分别设置传感器的节点数为25、30，四种算法的种群规模N均为20，迭代次数maxgen均为500，为了避免算法偶然性对实验的干扰，每组实验均进行20次，通过实验得到不同数量传感器节点的算法对比优化结果。

4.3. 算法对比优化结果及分析

实验结果如表1所示，从最终平均覆盖率来看，相比于其他三种算法，改进的粒子群算法在光纤传感网络的覆盖优化的各项性能均为最佳。其中在节点数为25时，最终平均覆盖率达到84%，相比于PSO、UPSO、IABC算法分别提高了4.91%、3.97%、3.96%。在传感器节点数为30时，改进的粒子群算法最终平均覆盖率达到90.77%，相比于PSO、UPSO、IABC算法分别提高了4.87%、3.54%、3.77%。

Table 1. Comparison between the algorithm and the PSO algorithm

表1. 四种算法对比结果

从目标区域的覆盖提升率来看，其中在节点数为25时，改进的粒子群算法的提升率为19.19%，相比于PSO、UPSO、IABC算法分别提高了5.54%、3.81%、4.73%。在传感器节点数为30时，改进的粒子群算法的提升率为16.46%，相比于PSO、UPSO、IABC算法分别提高了3.06%、2.08%、2.78%。

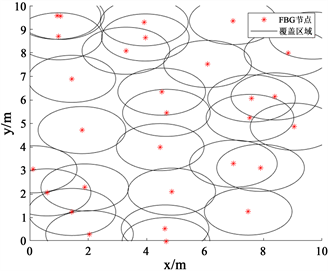
图5和图6分别为传感器节点数25和传感器节点数30的四种算法覆盖效果图，从图中可以直观的看出，PSO算法容易集中在某一区域，重叠区域较多，而UPSO算法虽然相比于PSO算法分散，但是覆盖的效果并不是特别理想。通过改进的粒子群算法优化后，传感器的节点在区域内分布较为均匀，相比于其他三种算法，重叠覆盖区域以及覆盖盲区都大大减少，覆盖效果有着明显的改善。

图7为四种算法的覆盖优化收敛曲线，从图中可以看出，无论是传感器节点数为25还是30，PSO算法初期收敛速度较快，但是在经历很少的迭代次数后就陷入局部最优解；而UPSO算法前期的寻优效果不如PSO算法，随着迭代次数的增加，该算法的寻优是能超过PSO算法，但是该算法整体收敛过程缓慢，全局寻优效果差；IABC算法在初期，是明显优于其他三种算法，但在经历了少数的迭代次数后，就陷入了局部最优解；从图7的收敛曲线可以看出本文改进的粒子群算法在一定的程度上是能够克服PSO算法以及IABC算法容易陷入局部最优解以及快速收敛的缺点，因此实验结果表明，在粒子数量相同及迭代次数一致的条件下，相比于PSO、UPSO、IABC算法本文改进的粒子群算法可以做到在有限的传感器数量下有效布置，并且提高测量精度减少覆盖空洞、最大程度的利用节点。

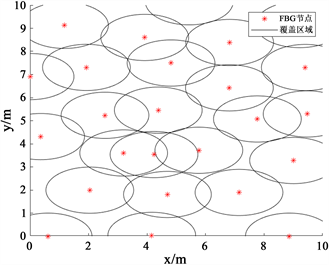(a) (b) (a) (b)

Figure 5. The number of sensors is 25, covering the optimization effect of (a) PSO; (b) UPSO; (c) IABC; (d) Improved particle swarm arithmetic

图5. 传感器数量为25覆盖优化效果。(a) PSO；(b) UPSO；(c) IABC；(d) 改进的粒子群算法

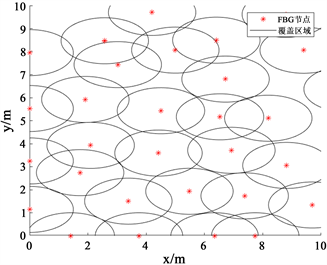(a) (b) (a) (b)

Figure 6. The number of sensors is 30, covering the optimization effect of (a) PSO; (b) UPSO; (c) IABC; (d) Improved particle swarm arithmetic

图6. 传感器数量为30覆盖优化效果。(a) PSO；(b) UPSO；(c) IABC；(d) 改进的粒子群算法

(a) (b)

Figure 7. Covering the optimization convergence curve. (a) The number of sensor nodes is 25; (b) The number of sensor nodes is 30

图7. 覆盖优化收敛曲线。(a) 传感器节点数为25；(b) 传感器节点数为30

5. 结束语

为了在有限的传感器数量下有效布置以提高测量精度、减少覆盖空洞、最大程度利用节点，本文提出了一种基于改进粒子群优化算法的光纤传感网络的覆盖优化，通过采用余弦自适应策略对惯性权重进行调整，并基于惯性权重对学习因子进行自适应调整。最后通过实验验证，证明了改进后的粒子群算法相比于PSO、UPSO、IABC算法，在光纤传感网络的覆盖优化方面具有更好的优化效果。通过仿真实验结果表明，本文提出的改进粒子群算法在传感器数量有限的情况下，能够有效提高光纤传感网络的覆盖率，实现更高的覆盖率，从而大大提高了测量精度，并减少了覆盖的空洞，能够做到最大程度的利用节点。今后的工作是尝试在粒子群算法适应度函数中加入选择算子的关联，进一步提高粒子群算法的收敛速度和精度。

基金项目

江苏省研究生实践创新计划项目(SJCX22_XY018)；国家自然科学基金资助项目(61873002)；江苏省产学研合作项目(BY2020445)。