1. 引言
步进电机作为一种将电脉冲信号转换成相应角位移的执行器件,具有定位精度高、动态力矩大、控制简单等特点,可以直接采用数字脉冲信号进行开环控制 [1] 。为了实现步进电机的平稳快速运动,提高电机加速能力以及减小启停过程对电机的冲击,防止失步,合理地加减速运行曲线设计是非常重要的。茹珂 [2] 提出了一种将传统弱磁控制方案应用于开环控制的方法,通过速度脉动反馈,消除了电机在低速运转时产生的振动,并在电机高速运转时增加了输出转矩,但其追求工作性能,大大增加了计算成本。周一飞 [3] 在MATLAB/Simulink仿真平台上根据步进电机的物理特性和数学算法模型建立了对应的电机仿真模型。该模型可通过修改电机技术参数使不同类型步进电机的相互转换,实现了一个模型通用化,也方便测试其他步进电机系统的性能,但模型过于理想,没有考虑实际运用中电流波动,机械震动等带来的影响。陈金龙 [4] 对普通S曲线加减速算法进行扩展,设计了多段S型曲线加减速算法,相比传统指数型加速,该算法能更好的拟合步进电机矩频特性,加减速过渡也更加平滑,减小了对系统的冲击及震动,但S型算法曲线由于算法复杂,计算时间较长,导致系统响应速度慢,不适用于实时系统。
本文利用Simulink软件,对步进电机控制系统进行仿真建模,设计了细分控制模型以及速度给定曲线模型,对比分析不同细分以及加减速算法对步进电机运行的影响。结果表明该仿真模型可有效提升步进电机的各种性能,也为预测其它步进电机系统的工作性能提供了一种途径。
2. 步进电机控制的数学模型
忽略定转子的漏磁、永磁体回路的漏磁、磁滞和涡流等因素的影响,即近似内部永磁体转子在相绕组中产生的磁链随转子位置正弦规律变化 [5] ,步进电机单相等效电路如下图1所示。
两相混合式步进电机平衡方程为:
(1)
(2)
(3)
(4)
,
分别表示A相跟B相的相电流和相电压,
是各相的绕线电阻,L是各相的电感,
为电机A、B相的反电动势,
为反电动势系数,
是电机的角速度,
为电机的机械角度,
为转子的齿数。
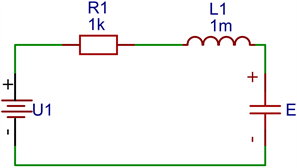
Figure 1. Equivalent circuit of stepper motor
图1. 步进电机等效电路
如图1,以a相为例,方程式中的首项表达式为a相绕组电流的电阻分压,第二项表达式是由转子的位置变化而引起a相绕组内磁场的变化而感应出的电势差,最后一项则为由电流变化引起的磁场变化而感应产生的电势差,即反电动势。
混合式步进电机的电磁力矩是由相电流、磁极之间的磁通量和永磁转子产生的磁电动势相互作用产生,其表达式如下:
(5)
混合式步进电机的机械动力学方程为:
(6)
其中,J是电机的转动惯量,B是电机的摩擦系数,
是电机外加的负载转矩。
最终通过式(1)~(6)可以得到两相混合式步进电机的基本数学模型,利用Simulink建立步进电机的开环控制系统仿真模型。仿真模型主要包括3个部分:加减速曲线及微步细分控制模块、PWM生成器模块、两相混合式步进电机简化模块,根据上述各个模块的功能,将各模块进行封装组合,最后得到如图2所示的仿真模型。
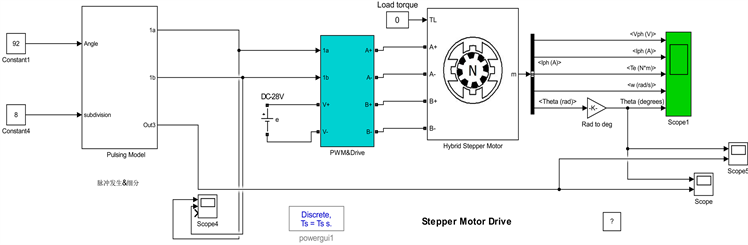
Figure 2. Simulation model of stepper motor
图2. 步进电机仿真模型
3. Simulink仿真模型的建立
3.1. 细分控制模型
为了防止步进电机运行过程中产生振动和失步,从而引进细分控制技术,使得步进角在运行中均匀变化,增加运行的稳定性 [6] 。电机细分驱动方式有很多,但是适合于两相混合式步进电机控制系统的最佳细分方式是恒转矩等步进角的细分驱动方式 [7] 。细分控制的实质就是把一个1.8˚的步进角细分成多步,将传统电流控制周期N等分,因此实际运行中转子的每个步进的角度是步进角的1/N,由此就可得到步进角
以及旋转D角度下所需总脉冲数S:
(7)
(8)
在等步进角细分控制中,绕组中的
两相电流波形的幅值会随细分数而实现调整,使得相电流的合成矢量在空间做幅值恒定的均匀旋转运动。细分后,绕组中的电流不再是之前的一对方波,而变成了一对阶梯正弦波,两相电流之间的相位差为90˚,输入电流通过拟正弦波的方式进行通断,转子按电流分成的台阶数旋转相同的次数。两相电流公式分别是:
(9)
(10)
其中,
是电机的额定电流,
是步进电机已运行的步数。
3.2. 细分控制模型的仿真验证
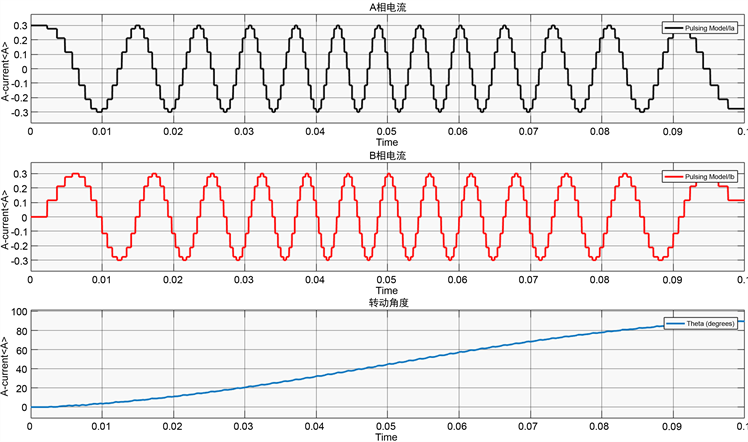
根据上述分析及搭建的细分驱动模型,驱动脉冲率设定为1000脉冲/秒,电机转动时间为0.1 s,分别模拟4细分、8细分、32细分工作模式下电流波形,比较不同细分对电机旋转角度的影响。如图3所示。
 (a) 4细分下的电流和转动角度波形
(a) 4细分下的电流和转动角度波形  (b) 8细分下的电流和转动角度波形
(b) 8细分下的电流和转动角度波形 (c) 32细分下的电流和转动角度波形
(c) 32细分下的电流和转动角度波形
Figure 3. Current and rotation angle waveform
图3. 三种不同工作模式下的电流和转动角度波形图
从图3可以看出,电流均呈现出明显的拟正弦波形,且随着细分数的增加,单步的步进角度减小,电流更接近正弦波形,线条趋于平滑,系统的分辨率也更高。每个细分工作方式下的实际转动角度都符合设计的目标角度,细分控制模块能够顺利满足电机的运行要求,说明设计正确。
3.3. 速度给定曲线模型
由于步进电机特殊的矩频特性,在启动过程中,如果启动频率不能满足负载运行的步进频率,步进电机就会出现失步或者不能运行的情况 [8] [9] 。因此电机的启停过程都需要一个过渡阶段以及加减速的过程,本文主要通过脉冲步法来对电机进行加减速控制,即通过等步数将位移曲线进行离散化,控制每个脉冲下电机的旋转角度。常见加减速曲线有直线型加减速、阶梯型加减速、抛物线加减速等,本文基于余弦函数设计了改进型S型加减速控制方案 [10] 。
如图4所示设计了S型曲线,
分别表示加速、匀速、减速三个阶段,
则对应每个阶段所需的运行步数,
表示电机正常工作的速度,
表示电机的加速度。
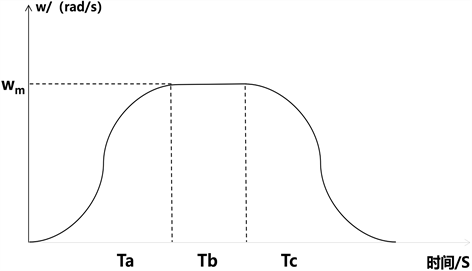
Figure 4. Improving the S-shaped acceleration and deceleration curve
图4. 改进S型加减速曲线
结合余弦函数,设计
加速阶段的加速度方程为:
(11)
对加速度方程进行积分可以分别得到速度方程和位移方程:
(12)
(13)
已知
,代入式(12)可得:
(14)
设定
是细分后的步距角,给定一个脉冲后转过的角度
,已知
,代入式(13)得:
(15)
(16)
式(16)即为第i个脉冲关于时间
的方程。采用牛顿迭代法,可以解得某个脉冲对应的结束时间,进而就可以得到每个脉冲所花的时间:
(17)
同理,可以得到匀速以及减速阶段每个脉冲对应的时间。匀速、减速阶段对应的速度曲线如下:
(18)
通过上面的计算,就可确定改进S型步进电机工作的速度和位置曲线。
3.4. 速度给定曲线模型的仿真验证
根据上述设计,将速度控制核心处理部分封装到Plusing Model模块中,算法用MATLAB中的M编程语言进行编译控制。本文选用三洋公司的两相混合式步进电机作为实验对象,其步距角为1.8˚,额定电压为28 V,通过最大转动角度实验和最短控制周期实验为例,分析对比梯形、抛物线、改进S型给定速度曲线三种不同控制方法的性能优劣性。
3.4.1. 最大转动角度实验
实验中分别采用梯形、抛物线、改进S型给定速度曲线作为系统的输入,设置系统控制周期100 ms,其中加速减速时间各为40 ms,匀速时间为20 ms,细分控制设置为16。在仿真过程中,逐步增大旋转角度D,从而获得三种不同曲线可达到的最大不失步转动角度。三种曲线的运行角度与时间的仿真结果如图5所示,Reality为实际位移,Theory为理论位移。
由图5的仿真结果可以看出,三种速度给定算法的理论曲线跟实际曲线都具有较高的重合度,在100 ms的相同时间内,步进电机输入梯形速度控制曲线所能达到的最大不失步转动角度为790˚,抛物线速度控制曲线的最大不失步转动角度为980˚,改进S型速度控制曲线的最大不失步转动角度为1140˚。
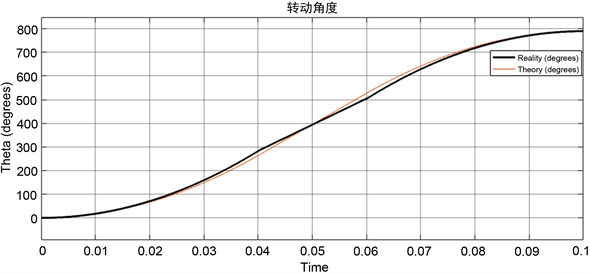 (a) 梯形控制位移曲线
(a) 梯形控制位移曲线 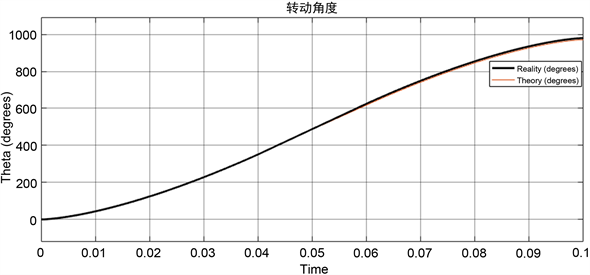 (b) 抛物线控制位移曲线
(b) 抛物线控制位移曲线  (c) 改进S型控制位移曲线
(c) 改进S型控制位移曲线
Figure 5. Displacement vs time curve
图5. 电机运行位移与时间关系曲线
给定转动角度为90˚,观察分析图6步进电机实际位移与理论位移的误差可以看出,当步进电机输入梯形速度控制曲线时,电机的位移误差为0.8˚;抛物线速度控制曲线的位移误差为0.24˚,改进S型速度控制曲线的位移误差为0.15˚。
 (a) 梯形控制位移曲线
(a) 梯形控制位移曲线 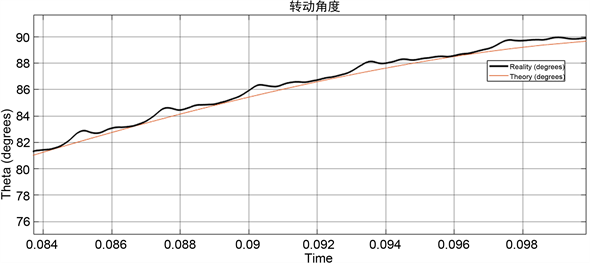 (b) 抛物线控制位移曲线
(b) 抛物线控制位移曲线 (c) 改进S型控制位移曲线
(c) 改进S型控制位移曲线
Figure 6. Displacement endpoint error result
图6. 位移终点误差结果
综上所述,在100 ms内,改进S型控制曲线的最大不失步角度为1140˚,比抛物线提高了16.3%,终点误差降低了37.5%,比梯形提高了44.3%,终点误差降低了81.5%。
3.4.2. 最短控制周期实验
该实验中分别采用梯形、抛物线、改进S型给定速度曲线作为系统的输入,设定步进电机的旋转角度为90˚,保持位移不变,等比例逐步减小控制时间,从而得到了三种速度控制曲线的最短控制周期。三种曲线的运行角度与时间的仿真结果如图7所示,Reality为实际位移,Theory为理论位移。
由图7的仿真结果可以看出,当设定运行角度为90˚时,梯形速度控制曲线到达指定位置的最短时间为52 ms,抛物线速度控制曲线到达指定位置的最短时间为42 ms,改进S型速度控制曲线到达指定位置的最短时间为42.4 ms。从而可以得出较梯形速度控制,改进S型控制曲线具有更短的运行时间,响应速度更快。
4. 上机验证
本文设计了以HC32F460为核心处理器的控制电路,在Keil5环境下进行编程开发,电路主要包括主控电路、电机驱动电路、编码电路、通讯电路、采样监测及过流保护电路 [11] [12] 。电机驱动电路采用集成步进电机驱动器SX7232M,该芯片内置微步进分度器,可直接使用对步进角度进行8细分,本设计通过HC32F460主控产生控制信号给SX7232M从而驱动步进电机转动,实现电机速度与位置的控制;通讯电路则采用的是CAN总线,CAN (CAN_RX, CAN_TX)信号通过CAN收发器ATA6561连接到主控HC32F460,主控对信号进行处理后产生步进电机驱动信号。硬件电路如图8所示。
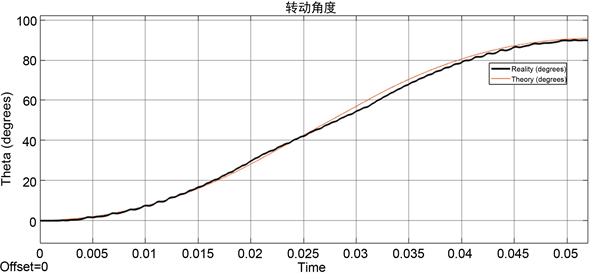 (a) 梯形控制位移曲线
(a) 梯形控制位移曲线 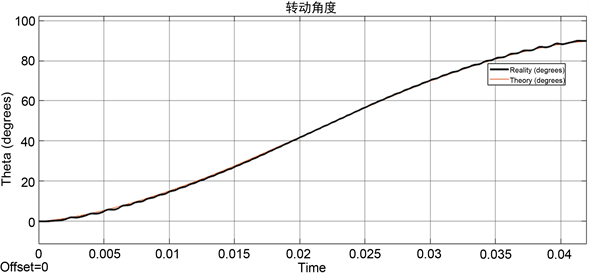 (b) 抛物线控制位移曲线
(b) 抛物线控制位移曲线 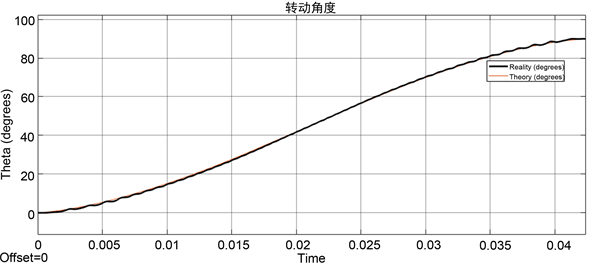 (c) 改进S型控制位移曲线
(c) 改进S型控制位移曲线
Figure 7. Shortest time simulation results
图7. 最短时间仿真结果
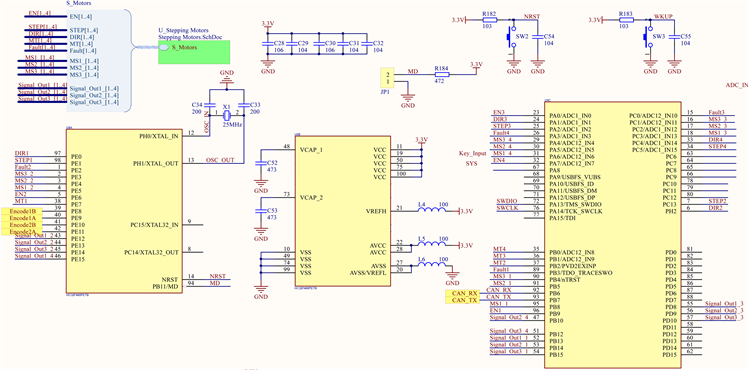
Figure 8. Motor hardware drive circuit
图8. 电机硬件驱动电路
以袜机缝合机构中的缝齿盘为实验对象,缝齿盘的工序是将转移之后的袜头线圈通过旋转半环支架翻转180˚,翻转图如图9(b)所示,将上下缝刺一对一对齐,缝头机进行袜头最后的自动缝合。该过程就需要步进电机具有极高的精度,能不失步的运动到指定位置,才能满足袜机缝合的要求,如果角度偏差太大,会导致缝合失败或者产品质量不达标,影响企业的效益。
 (a) 缝齿盘结构
(a) 缝齿盘结构 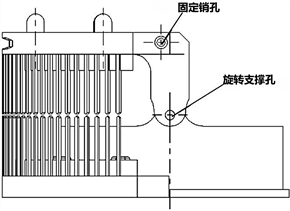 (b) 缝齿盘翻转定位图
(b) 缝齿盘翻转定位图
Figure 9. Suturing mechanism
图9. 缝合机构
为了验证改进S型速度控制曲线的优劣线,通过Altium Design将原理图进行PCB设计并加工成实物电路控制板,将上述速度控制曲线编写成C语言,搭建步进电机测试平台。
实际生产中,只需要缝齿盘旋转180˚,所以实验验证中就以180˚为测试的旋转角度,每组重复100次,测试分析梯形、抛物线、改进S型给定速度曲线在运行终点的位置与实际需要角度之间的偏差,从而判断各个曲线的优劣性。由图10的仿真结果可以看出,梯形控制速度曲线的误差在−2.9˚~2.7˚之间,抛物线控制速度曲线的误差在−1.1˚~1˚之间,而改进S型速度控制曲线的误差在−0.4˚~0.3˚之间,由此可以看出,实际运行效果与仿真结果一致,改进S型速度控制曲线精度更高,控制效果更好。
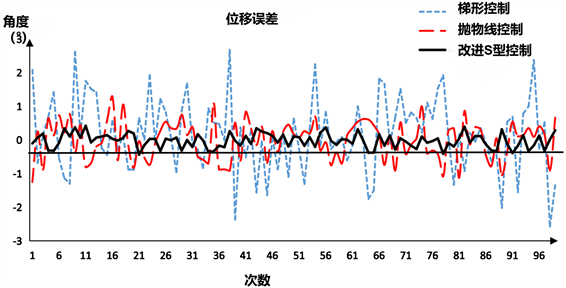
Figure 10. Simulation results of three types of curve errors
图10. 三种曲线误差仿真结果
5. 结论
本文从缝合机构的工作特性入手,根据所用两相混合式步进电机的电气特性和机械特性,构建了恒转矩等步进角细分的步进电机开环控制模型,步进角细分的越小,电机运行的越平稳,位移线条也越趋于平滑。通过对步进电机不同的加减速控制算法的仿真结果分析,改进S型速度控制曲线的速度和加速度都具有连续可导性,且该算法在给定时间内具有最大的不失步转动角度,大大提高了步进电机的响应速度和运行精准度。综上可以得出,改进S型速度控制曲线在步进控制中能够改善步进电机的运行精确性和平稳性,适用于袜机缝合机构等对步进电机运行平稳和位置精度具有较高要求的场合。
致谢
首先我要感谢我的导师彭来湖和史伟民,是他们渊博的专业知识、严格的科研态度、严谨的教学精神才促使我能够圆满的完成本论文的撰写。其次我要感谢我同公司的未印,牛冲师兄,是他们给予我实验调试的条件。最后我要感谢本文借鉴的资料、图片、文献、研究思想和设想的所有作者,感谢我的朋友同学们,本论文的顺利完成离不开各位的关心和帮助。在此,我谨向所有对给予我帮助的老师,同事,朋友致以我最真挚的诚意和最衷心的感谢!
NOTES
*通讯作者。