基于碳排放流理论的梯级水风光储一体经济调度

Economic Scheduling of a Cascade Hydro-Wind-Photovoltaic-Storage System Based on Carbon Emission Flow Theory

摘要: 为分析梯级水风光储一体化发电模型对电力系统的低碳贡献，本文构建了梯级水风光储一体化低碳经济调度系统。首先，考虑系统经济性，将包含碳交易成本等在内的系统综合成本最小设定为目标函数。其次，对该模型进行求解，运用碳排放流理论对于节点碳势、节点碳流率以及节点总碳流率进行计算，分析梯级水风光储一体化模型对于低碳电力的作用。最后，借助算例IEEE30节点系统的求解结果，分析梯级水风光储一体化模型的经济性能。算例结果表明，所提梯级水风光储一体化调度模型在低碳性和经济性均具有良好表现。

Abstract: In order to analyze the low-carbon contribution of integrated a Cascade Hydro-Wind-Photovoltaic- Storage System power generation to the power system, this paper constructs a low-carbon economic dispatch system for a cascade Hydro-Wind-Photovoltaic-Storage (CHWPS) system. Firstly, having taken system economy into consideration, the minimization of the integrated system cost including carbon trading cost is set as the objective function. Secondly, the model is solved, and the carbon emission flow theory is applied to calculate the node carbon potential, node carbon flow rate and node total carbon flow rate to analyze the role of the cascade Hydro-Wind-Photo- voltaic-Storage system model for low-carbon electricity. Finally, the economic performance of the cascade Hy-dro-Wind-Photovoltaic-Storage system model is analyzed with the help of the solving results of the IEEE 30-node system. The results of the example show that the proposed cascade Hy-dro-Wind-Photovoltaic-Storage system scheduling model has good performance in terms of low-carbon and economic efficiency.

1. 引言

电力系统低碳运行是实现能源结构转型的关键环节。在电力行业，分析系统碳排放量可更好地进行低碳分析。目前，在电力系统中，碳排放量这一概念仅从宏观角度出发统计能源消耗量，虽然具备结果直观的优点，仍无法准确描述电力系统低碳特征。基于电力系统潮流分布的概念，文章 [1] 提出了电力系统碳排放流这一理念，并用其来进行理论分析，结果在空间尺度上证明了碳排放流的分析价值，对未来电力行业进行低碳发展与规划将起指导作用。之后，文献 [2] 结合电力系统潮流计算于网络分析法，给出了电力系统碳排放流的计算方法，并进行了正确性验证。

近年来，风光等新能源并网时所引起的出力不确定性为碳排放流分析研究增加了一定难度。研究 [3] 建立了风电注入功率对碳排放流分布的影响模型，得到了此种情况下系统中碳排放流的不确定特征。研究 [4] 则计算了光伏注入功率对系统节点及各支路的影响因子，分析其对电力系统碳排放流的分布影响。研究 [5] 同时考虑了风光储联合运行下的电力系统碳排放流分布，实现新型电力系统低碳优化调度。然而，尚未有研究针对梯级水风光储一体化电站进行展开。

本文从推进梯级水风光储一体化基地建设的角度出发，以系统综合成本最小为目标函数进行电力系统经济调度求解计算，借助碳排放流理论，将梯级水风光储一体化对于降低碳排放量以及缓解机组碳排压力的作用可视化处理，并解释其原因。除此之外，从低碳性和经济性两个角度对所提梯级水风光储一体化调度模型进行求解，并设置两种其他场景进行对比证明其适应性和表现力，可为推进梯级水风光储一体化基地建设提供指导意见。

2. 梯级水风光储一体化经济调度模型

2.1. 目标函数

为考虑电力系统整体经济性，本模型的优化目标为综合成本最小。

$\min F={\displaystyle \underset{t=1}{\overset{T}{\sum }}{\displaystyle \underset{i=1}{\overset{N_G}{\sum }}{f}_G}}+f_S+f_E+f_C$ (1)

式中：F为系统综合成本；f_G、f_S为火电机组和电池储能机组的运行成本；f_E为碳交易成本；f_C为弃风弃光成本；T为调度周期；N_G为火电机组数。

1) 火电机组运行成本

$f_G=a_i{P}_{i,t}^2+b_i{P}_{i,t}+c_i$ (2)

式中：a_i、b_i、c_i为火电机组i的耗量系数，P_i,t为火电机组i在t时段的有功出力值。

2) 电池储能机组运行成本

$f_S=\frac{1}{P_{sn}{T}_a}{C}_{cap}\frac{r{\left(1+r\right)}^n}{{\left(1+r\right)}^n-1}\left|P_{sd,t}-P_{sc,t}\right|$ (3)

式中：P_sn为电化学储能机组装机容量；T_a为机组年运行小时数；C_cap为投资成本；r为折旧率；n为使用寿命；P_sc,t、P_sd,t为t时段内充放电的功率。

3) 碳交易成本

$f_E=\sigma \left(E_P-E_q\right)$ (4)

$\{\begin{array}{l}{E}_P={\displaystyle \underset{i=1}{\overset{N}{\sum }}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{M}_{it}{P}_{it}}}\\ E_q=\epsilon {\displaystyle \underset{t=1}{\overset{T}{\sum }}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\eta P_{i,t}}}\end{array}$ (5)

式中： $\sigma$ 为单位碳交易价格；E_P为总碳排放量；E_q为系统碳排放额度； $\eta$ 为单位电量排放基准。

4) 弃风弃光成本

$f_C=C_{cur}\cdot \left[\left(P_{w,t,pre}^{}-P_{w,t}\right)+\left(P_{p,t,pre}^{}-P_{p,t}\right)\right]$ (6)

式中：C_cur为弃风弃光成本系数；P_w,t,pre、P_p,t,pre分别为t时段内风电、光伏机组预测出力；P_w,t、P_p,t分别为t时段内风电、光伏机组的实际出力。

2.2. 约束条件

为充分利用能源，减少弃能，本文提出梯级水风光蓄一体出力发电模型，其中包含梯级水电机组、风电机组、光伏机组、抽蓄机组，模型示意图如图1。

1) 水电机机组出力约束

$\begin{array}{l}P{h}_{i,\min }\le P{h}_{i,t}\le P{h}_{i,\max }\\ Q{h}_{i,\min }\le Q{h}_{i,t}\le Q{h}_{i,\max }\\ V{h}_{i,\min }\le V{h}_{i,t}\le V{h}_{i,\max }\end{array}$ (7)

$V{h}_{i,\max }=V{h}_{i,t-1}+\left(I{h}_{i,t}-Q{h}_{i,t}+Q{h}_{i-1,t}\right)$ (8)

式中：Ph_i,max、Ph_i,min为水电站i出力的上下限；Qh_i,max、Qh_i,min为水电站i的流量上下限；Vh_i,max、Vh_i,min为水电站i的水库容量上下限；Ih_i,t为水电站i在t时段的自然流入水量。

2) 风电、光伏电机组出力约束

$\begin{array}{l}0\le P_{w,t}\le P_{w,t,pre}\\ 0\le P_{p,t}\le P_{p,t,pre}\end{array}$ (9)

式中：P_w,t、P_p,t分别为风电、光伏机组在t时段的出力；P_w,t,pre、P_p,t,pre分别为预测的风电、光伏机组出力。

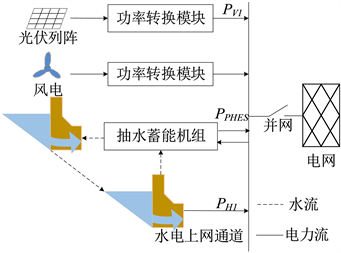
Figure 1. Hydro-Photovoltaic-Pumped power generation model

图1. 梯级水风光储一体发电模型

3) 抽水蓄能机组出力约束

$\begin{array}{l}{P}_{hg,\min }\le P_{hg,t}\le P_{hg,\max }\\ P_{hp,\min }\le P_{hp,t}\le P_{hp,\max }\\ E_{h,\min }\le E_{h,t}\le E_{h,\max }\\ E_{h,t+1}=E_{h,t}+\left({\eta }_p{P}_{hp,t}-{\eta }_g{P}_{hg,t}\right)\end{array}$ (10)

式中：P_hg,max、P_hg,min分别表示抽蓄机组的发电功率上下限；P_hp,max、P_hp,min分别表示抽蓄机组的抽水功率上下限；E_h,t表示抽蓄机组在t时段的上水库水位；E_h,max、E_h,min分别表示抽蓄机组在t时段的上水库水位上下限； ${\eta }_p$ 、 ${\eta }_g$ 表示抽水与发电转换系数。

4) 电池储能机组运行约束

$W_{B,\min }\le W_{i,B}\le W_{B,\max }$ (11)

$\begin{array}{l}0\le P_{sc,t}\le P_{c,\max }\\ 0\le P_{sd,t}\le P_{d,\max }\end{array}$ (12)

式中：W_B,min、W_B,max分别表示储能机组可容纳电量上下限；P_c,max、P_d,max分别表示储能机组在t时段最大充放电量；P_c,t、P_d,t为储能机组在t时段充放电功率。

5) 功率平衡约束

${\displaystyle \underset{i=1}{\overset{N}{\sum }}{P}_{i,t}}+P_{CHWP,t}-P_{sc,t}+P_{sd,t}={\displaystyle \underset{d=1}{\overset{N_L}{\sum }}{P}_{d,t}}$ (13)

式中：P_i,t为火电机组i在t时段出力；N为火电机组台数；P_CHWPS,t为梯级水电及风光在t时刻出力；P_sc,t为储能机组在t时段充电功率；P_sd,t为储能机组在t时段放电功率；P_d,t为节点d在t时段的典型日负荷；N_L为负荷节点数。

6) 火电机组运行约束

$\begin{array}{l}{P}_{i,\min }\le P_{i,t}\le P_{i,\max }\\ 0\le {\delta }_{i,t+}\le {\delta }_{i,\max +}\\ 0\le {\delta }_{i,t-}\le {\delta }_{i,\max -}\end{array}$ (14)

式中：P_i,max、P_i,min分别为火电机组i在t时段有功功率的上下限； ${\delta }_{i,t+}$ 、 ${\delta }_{i,t-}$ 分别为火电机组i在t时段增加、减少的爬坡容量； ${\delta }_{i,\max +}$ 、 ${\delta }_{i,\max -}$ 分别为火电机组i在t时段可增加、减少的最大爬坡容量。

7) 线路容量约束

受端电网各线路的输电功率不应超过线路的最大输电容量，即

$0<P_{L,t}<P_{L,\max }$ (15)

式中：P_L,t为t时段线路的输电功率；P_L,max为电路的最大输电容量。

3. 电力系统碳排放流理论

为明确不同发电机对于电力系统潮流网络的碳排放责任，文献 [1] 提出了碳排放流这一概念。碳排放流依附于电力潮流，由电力系统维持支路潮流碳排所形成的虚拟网络流，由发电侧产生，随系统潮流在网络中进行流动，最终流向用户侧。碳排放流依附于系统有功潮流，在电力系统中，由发电侧随着系统潮流流入用户侧消费终端。为衡量电力系统碳排放流，以下几个指标经常被用来计算相关信息。

3.1. 节点碳势

节点碳势I_NCEi为节点i消费单位电量所对应发电侧的碳排放量，用来表征该节点的碳排放强度，表达式如下：

$I_{\text{NCE}i}=\frac{{\displaystyle \underset{l\in N^{+}}{\sum }{R}_l}}{{\displaystyle \underset{l\in N^{+}}{\sum }Plin{e}_l}}$ (16)

式中：Pline_l为支路l的有功潮流；N⁺为有潮流流入节点i的支路集合。

3.2. 支路碳流率

碳流率R_i定义为支路i在单位时间内随潮流而通过的碳流量。公式如下：

$R_i=\frac{\text{d}{F}_i}{\text{d}t}$ (17)

式中：F_i为支路i上碳排放流所对应的碳排放累积量的大小。

3.3. 系统总碳流率

系统总碳流率为电力系统所有节点碳流率的总和，表达式如下：

$R_{all}={\displaystyle \underset{i=1}{\overset{n}{\sum }}{R}_i}={\displaystyle \underset{i=1}{\overset{n}{\sum }}{P}_{G_i}{e}_{G_i}}$ (18)

式中：n为电力系统节点数；R_all为电力系统节点碳流率总和；R_i为节点i的碳流率；P_Gi为节点i的发电机组输入有功功率；e_Gi为节点i的发电机组碳排放强度。

4. 算例分析

4.1. 基础数据

本文借助修改后的IEEE-30节点系统进行算例分析，如图2所示。该发电系统包括6台火电机组、1个梯级水风光储一体化出力电站。其中，梯级水风光储一体化出力电站包含3个梯级小水电机组、1个风电机组、1个光伏机组以及一个储能机组，并网节点编号为3。梯级水电机组参数见表1。水风光规模及电池储能机组参照论文 [6] 进行设定。本文负荷典型日选择负荷较大的夏至日，以1小时为一个调度时段。典型日的负荷、风电机组和光伏机组出力的曲线如图3所示。

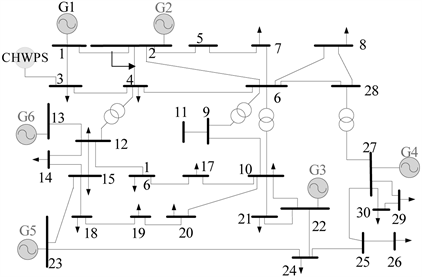
Figure 2. A modified IEEE 6-machine and 30-bus system

图2. 一个修改的IEEE6机30节点系统

Table 1. Parameters of cascade hydroelectric plants

表1. 梯级水电机组参数

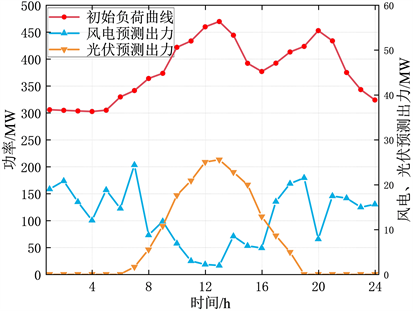
Figure 3. Wind power, photovoltaic forecast output and typical daily load curve

图3. 风电机组、光伏机组预测出力及典型日负荷曲线

为更好地证明所提模型的优越性，本文设置3个场景。场景一：考虑梯级水风光一体化发电。场景二：在场景一的基础上加入电池储能电站，考虑梯级水风光储一体化发电。场景三：在场景一的基础上加入抽水蓄能电站，考虑梯级水风光蓄一体化发电。

4.2. 求解结果分析

对所设置的三种场景分别进行求解计算，得到如图4~6所示的三种机组最优出力结果。

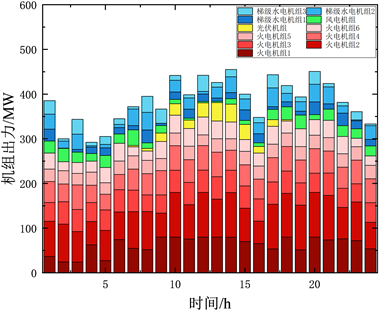
Figure 4. Distribution of optimal output for each unit under Scenario 1

图4. 场景一下各机组最优出力分布

由图4可以看出，火电机组各机组稳定发挥，其出力占据主要地位。由于一级梯级水电站初始来水量不稳定以及次级水电站各时段来水量由上一级梯级水电站决定，梯级水电站出力具备一定约束。图4直观展示了风光出力时所具有的不确定性。对于风电机组，受风速影响，在0时至9时具备较高出力，之后风速降低，其出力开始减少，直到17时回升至较高水平。而对于光伏机组，从7时开始缓慢出力，9至15时有较高出力，但在其他时段失去了发电的能力，出力为0。

Figure 5. Distribution of optimal output for each unit under Scenario 2

图5. 场景二下各机组最优出力分布

由图5可知，当电池储能电站接入系统后，降低了火电机组的出力，从而缓解了火电机组的碳排放压力，也为系统灵活运行提供了电力储备。在满足负荷需求的情况下，将多余的系统出力储存起来，降低弃风弃光量；在负荷高峰将储存电量发出，缓解机组压力。此种情况下，由于储能机组的调峰填谷作用，整个系统将更具灵活性。

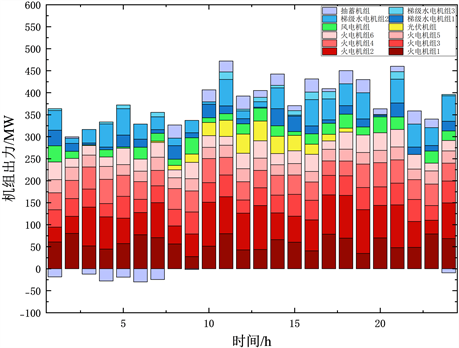
Figure 6. Distribution of optimal output for each unit under Scenario 3

图6. 场景三下各机组最优出力分布

图6为场景三下求出的各发电机组最优出力。在此场景下，由于抽水蓄能电站代替电储能电站参与调度，在0~8时负荷低峰时逐渐储存多余电量，在用电高峰不断发电缓解其余机组压力。

4.2.1. 不同场景下的节点碳势与节点碳流率

三种场景下的IEEE-30改进算例下的节点碳势如表2所示。

Table 2. Distribution of node carbon potential for each scenario

表2. 不同场景下的节点碳势分布

如表2所示，由于梯级水风光储一体化电站接入节点3，其机组碳排放强度为0，不产生二氧化碳排放，故其节点注入碳流率为0。场景三中所有火电机组所在节点碳势相比其他两个场景较低，节点碳势越低，代表在该结点处消费单位电量所对应的发电机组碳排放量越低。

由节点碳势得出系统各支路节点碳流率之后，可继续计算出三种场景下的IEEE-30改进算例下的节点碳流率，如表3所示。

Table 3. Distribution of branch carbon emission flow rate for each scenario

表3. 不同场景下的节点碳流率分布

如表3所示，场景三中所有火电机组所在节点碳流率相比其他两个场景较低，节点碳流率越低，代表在该节点处单位是界内随单位有功潮流通过的碳流量越低。

三种场景下的IEEE-30改进算例下的节点总碳流率如表4所示。

Table 4. Total carbon flow rate of nodes for each scenario

表4. 不同场景下的系统总碳流率分布

由表4可知，场景三所提出的模型节点总碳流率最低，并相对于场景一降低了20.7067 t(CO₂)·h⁻¹，相对于场景二降低了17.7591 t(CO₂)·h⁻¹。表2~4证明相比于场景一和场景二而言，使用抽水蓄能的梯级水风光储一体化模型对于发电机组碳排压力的缓解作用最强。

4.2.2. 不同场景下的经济性对比

在本文所建立的梯级水风光储一体化经济优化调度模型基础上，对本文所设置的三个场景分别进行求解，得到各场景优化调度结果如表5所示。

Table 5. Optimised scheduling results for each scenario

表5. 各场景下优化调度结果

对比场景1和场景2可知，当电池储能一起参与场景调度时，综合成本下降了4.14万元，碳排放量减少了486.4吨，碳交易成本降低了0.31万元，弃风弃光量降低了18.08%。这是因为储能电站具有出色的适应性和可操控性。它不仅能够部分弥补风电和光伏电站产生的间歇性和波动性，还可以降低火电机组的负荷，并带来环境效益。由此可见，当储能机组参与电力系统调度时，能够为系统带来一些经济性，同时也将多余的风电光伏储存起来，使电力系统更加具备灵活性。对比场景2和场景3可知，梯级水风光蓄一体发电时，抽水蓄能电站在负荷低谷时抽水储存电量，在负荷高峰时作为电源补给，实现了对弃风弃光电量的时空转移，从而有效地降低负荷的峰谷差。同时，抽水蓄能电站提供部分备用容量，有助于缓解火电机组的调节压力。此时，综合成本下降了4.14万元，碳排放量减少了486.4吨，弃风弃光量降低了13.70%。场景对比结果表明，梯级水电、风机发电、光伏发电和抽水蓄能电站四者联合发电功率输出的互补性优于梯级水风光互补及梯级水风光储功率输出的互补性。

5. 结论

1) 本文运用碳排放流理论，分析不同模型场景下的碳排放流指标，如节点碳势、节点碳流率以及节点总碳流率，计算结果表明，由抽水蓄能参与的梯级水风光储一体化电站发电机组缓解碳排压力的作用最大，从这一理论基础证明所提梯级水风光储一体化调度模型对低碳电力发展的作用。

2) 通过对比本文所设置三种模型场景的经济成本以及碳交易成本，可知由抽水蓄能参与的梯级水风光储一体化电站综合成本最低，经济性表现最好，进一步证明所提出的梯级水风光储一体化调度模型的优越性。

基金项目

贵州省科技支撑计划项目([2023] 329)；贵州省科技支撑计划项目([2023] 290)。

NOTES

^*通讯作者。