金属化纤维电磁防护复合材料拉伸强度及失效研究

Research on the Metal-Coated Fiber Electromagnetic Shielding Composites Tensile Strength and Failure

摘要: 本文以镀镍碳纤维作为主要增强材料；基于经典层合板理论进行了材料建模和性能参数设定，采用Hashin准则作为材料的失效行为判据，对该材料的拉伸强度进行了数值计算。用热压罐成型工艺制备了金属化纤维电磁防护复合材料，对该材料的室温拉伸强度性能进行了实测。对数值计算结果和实测结果进行分析对比，发现两者较为吻合，实现对电磁防护复合材料的力学和失效性能进行有效预判，从而缩短产品的结构力学设计周期。

Abstract: The electromagnetic shielding composites are composed of the nickel-coated carbon fibers as the main enforced material. Based on the classical laminate plate theory, the modeling and the simulation were done by FEA analysis. The tensile strength of the material was calculated by Hashin damage criteria which can predict the damage evolution effects. The composites test samples were prepared under autoclave process. The result of tensile strength of the composite was obtained by real test. By comparing the tensile calculation result and real test result, we found that calculation result fits the real test results well and the method can predict the strength and failure performance effectively and shorten design period of the structural products.

1. 引言

当前行业对碳纤维复合材料的力学性能和失效行为研究较为广泛，但对金属化碳纤维增强复合材料的力学性能的报道相对较少。纤维增强复合材料的力学性能参数一般采用试验的方式进行采集，耗费大量开发时间和试验经费。因此利用数值计算和模拟方法来对材料的力学性能进行预判，可有效缩短研发周期，同时可对产品的轻量化设计提供数据依据。

2. 研究进展

国内外利从事纤维增强复合材料建模和强度计算的研究较为广泛。根据材料的应用场景不同，目前的研究热点主要集中在材料的损伤与失效行为。孔祥宏等 [1] 针对含损伤复合材料泡沫夹层板，提出使用Abaqus/CAE进行参数化建模，得到了有限元渐进损伤强度分析的结果与实验结果相吻合的结论。薛康等 [2] 提出了基于连续介质损伤力学(CDM)的单向纤维增强聚合物复合材料压缩破坏渐进损伤分析(PDA)模型，通过用户材料子程序接口VUMAT引入到有限元软件中实现了有限元求解。

3. 复合材料层合板结构建模与仿真分析

3.1. 复合材料的层合板结构建模

经典复合材料强度理论一般以层合板作为研究对象，拉伸强度和拉伸模量作为单向层合板的主要力学性能指标，是产品结构力学设计的基本参数。对于纤维增强复合材料，拉伸强度的求解一般需要提供材料的基本性能参数，以该性能参数作为材料力学性能计算的依据，同时还需要给出基于材料渐进损伤和失效的判据，以模拟材料样件拉伸试验中的断裂情况。

本文中的复合材料增强相是金属化纤维纱线。以单向层合板为研究对象，该材料的几何结构主要由纱线和树脂基体构成。根据《GB1447-2005纤维增强塑料拉伸性能试验方法》中对拉伸强度试验样条制备要求，对I型样条进行了层合板模型建模。样条的形状如图1所示，厚度为2 mm。

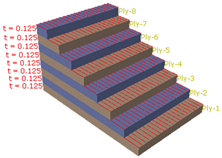
Figure 1. The modeling of strength simulation and ply stack display

图1. 力学仿真模型建模和铺层示意

3.2. 材料参数和失效准则

复合材料的力学性能参数如表1所示。本文以材料弹性属性lamina作为材料的基本参数，以材料的轴向断裂强度X^T，Y^T、径向断裂强度X^C，Y^C，剪切断裂强度S^T，S^L为材料的强度参数，结合失效扩展参数，对模拟计算中使用的材料参数进行设定。

Table 1. The strength parameters of the metal-coated carbon fiber composite

表1. 金属化纤维复合材料力学性能参数

选取复合材料Hashin失效准则作为样件断裂的依据。Hashin失效准则提出了4类复合材料失效模型，分别对应了增强纤维和树脂基体两相材料的失效模型。

1) 纤维拉伸断裂：

$F_{ft}={\left(\frac{{\hat{\sigma }}_{11}}{X^T}\right)}^2+\alpha {\left(\frac{{\hat{\sigma }}_{12}}{S^L}\right)}^2=1$

2) 纤维压缩缩聚和褶皱：

$F_{mc}={\left(\frac{{\hat{\sigma }}_{22}}{2S^T}\right)}^2+\left[{\left(\frac{Y^C}{2S^T}\right)}^2-1\right]\frac{{\hat{\sigma }}_{22}}{Y^C}+{\left(\frac{{\hat{\sigma }}_{12}}{S^L}\right)}^2=1$

3) 树脂基体拉伸断裂：

$F_{fc}={\left(\frac{{\hat{\sigma }}_{11}}{X^C}\right)}^2=1$

4) 树脂基体压缩破裂：

$F_{mt}={\left(\frac{{\hat{\sigma }}_{22}}{Y^T}\right)}^2+{\left(\frac{{\hat{\sigma }}_{12}}{S^L}\right)}^2=1$

其中在失效出现前，其数值为0；在失效开始后，其数值变为1。上述4个数值的由0变为1，可计算模拟出样条的失效起始时间，同时可得到基于位移载荷施加下的应力曲线。利用该曲线可以模拟计算出该材料的拉伸强度。

3.3. 仿真分析

根据标准中的规定，本文对拉伸强度试验样条的某一侧施加载荷设置为10 mm/min轴向载荷，另一侧采用固支方式限定其各向自由度。由于在模拟计算时，出现了材料的断裂失效，利用显示求解方式，可极大地降低模拟计算的不收敛性，因此本文主要采用了显示迭代方式进行计算。

对拉伸样条模型进行网格划分，由于失效发生在纺锤形样条的中部，因此样条两端的网格可适当粗大，对样条中部的网格划分需要精细。划分网格后的模型效果如图2所示。

Figure 2. The meshing for modeling

图2. 模型的网格划分

3.4. 仿真结果

拉伸试样模型在Step time为0.85 s时出现了失效现象，在样条的测试有效区域出现了撕裂，经过0.05 s后彻底被拉伸断裂，如图3所示。在仿真模拟计算中，采用了基于能量的损伤扩展方法和元素删除方法，实现了对纤维复合材料的拉伸断裂模拟。

Figure 3. The simulation contour of the sample’s tensile failure

图3. 样条拉伸断裂应力云图

金属化纤维织物复合材料的应力–时间曲线如图4所示。

通过分析图3和图4中拉伸断裂部位的应力云图和应力–时间曲线可知，金属化纤维复合材料在位移载荷开始施加的一定时间内，其值均未达到 ≥ 1的初始失效条件，因此并未发生失效破坏，在Step time为0.85 s时值率先达到并超过了1，此时树脂基体先发生了失效破坏，演化之后纤维出现了局部失效，最终演化成了试样的整体拉伸断裂。

4. 金属化纤维复合材料拉伸强度测试和结果

采用热压罐工艺进行了金属化纤维复合材料的制备。采用《GB1447-2005纤维增强塑料拉伸性能试验方法》 [3] 进行测试，测试样条形状如图5所示，样件尺寸：L = 180 mm，L₀ = 50 mm，L₁ = 55 mm，L₃ = 120 mm，b = 10 mm，b₁ = 20 mm，d = 2 mm。

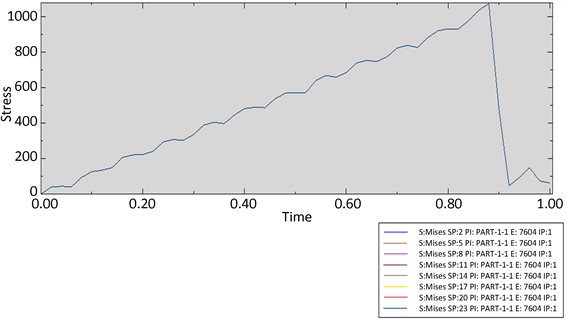
Figure 4. The stress-time curve of the sample

图4. 样条的应力–时间曲线

Figure 5. The shape of the test sample

图5. 测试样条形状

选取同批次一组5支样条进行了拉伸测试，取平均值得到拉伸强度结果为957 MPa。金属化纤维复合材料拉伸强度数值计算结果为1094 MPa，比实测结果高137 MPa，偏差百分比在85%左右。此类偏差的主要产生原因应为在模拟计算中使用的模型均为理想模型，而实际测试采用的制备样品中会存在微小瑕疵，造成离散性偏差大，因而实测值一般会低于模拟计算值。一般15%以内的计算偏差可以认为实测结果与仿真结果较为吻合。

5. 结论

采用数值分析计算方法对金属化纤维增强复合材料的拉伸性能进行计算，失效依据采用了Hashin失效准则，模拟了材料在拉伸试验中的断裂破环。仿真结果与实测结果较为接近。

综上所述，采用数值模拟计算的方法对金属化纤维复合材料力学强度性能计算和失效模拟是可行有效的，可作为金属化纤维复合材料力学性能设计的参考依据。