关联规则挖掘中闭频繁项集的理解与探索

Understanding and Exploration of Closed Frequent Itemsets in Association Rule Mining

摘要: 关联规则挖掘，通过数据挖掘事务之间的关联关系，被广泛应用到各个领域，主要是通过频繁项集产生关联规则，而频繁项集的挖掘又归结到闭频繁项集的挖掘，由此可见闭频繁项集在关联规则挖掘种的重要作用。本文以购物篮关联规则分析为场景，对闭频繁项集的理论进行了梳理，针对闭包算子定义中的函数i和t进行了单调性证明；对闭包算子定义满足的三条性质进行了证明；对频繁项集和其闭包的支持度进行了探讨；对封闭频繁项集和其超集之间的支持度进行了关系讨论。最后，按照频繁项集及其闭包所形成的等价类的性质进行了研究，给出了有关定理和证明，以及结论等。

Abstract: Association rule mining, is widely used in various fields by mining the association relationships between transactions through data mining, in which, association rules are mainly generated through frequent itemsets, and the mining of frequent itemsets is reduced to the mining of closed frequent itemsets, and this shows the important role of closed frequent itemsets in association rule mining. This article takes the analysis of shopping basket association rules as a scenario to sort out the theory of closed frequent itemsets, and proves the monotonicity of functions i and t in the defi-nition of closure operators; proves three properties that the closure operator definition satisfies; explores the support of frequent itemsets and their closures; discusses the relationship between the support of closed frequent itemsets and their supersets. Finally, the properties of the equiva-lence class formed by the frequent itemsets and their closure are studied, and relevant theorems, proofs, and conclusions are provided.

1. 引言

频繁项集挖掘最早是由Agrawal等 [1] 于1994年在挖掘关联规则的Apriori算法中提出来的，该算法对顾客的购物篮数据进行分析，进而通过频繁项集产生强关联规则，分析顾客在购物篮中放置的不同物品之间的联系来分析顾客的购买习惯。然后，关联规则挖掘被应用到各个领域，比如：蛋白质DNA结合序列模式的发现 [2] ，教育中的学生管理 [3] ，临床事件的提取和可视化 [4] ，动物迁徙的优化 [5] 等。

对大型事务数据集进行频繁项集挖掘的一个主要挑战是：满足最小支持度阈值的频繁项集往往数量较大，尤其是最小支持度阈值的设置较低时。这是因为当一个项集是频繁项集时，其包含的子项集也都是频繁项集，而大的频繁项集往往包含指数规模的子频繁项集。为解决这一问题，学者们提出了闭频繁项集和最大频繁项集的挖掘算法 [6] [7] 。闭频繁项集与最大频繁项集提供了完全频繁项集的紧凑表示，同时闭频繁项集还提供了项集的支持度信息 [8] [9] ，即一个项集和它的闭项集有相同的支持度 [10] 。这样，挖掘关联规则的第一步就转变为找出所有闭频繁项集。挖掘闭频繁项集也主要分为两步：(1) 找出频繁项集；(2) 检查频繁项集是否是闭集。

挖掘闭频繁项集的算法方面进展比较多 [11] [12] [13] [14] ，闭频繁项集挖掘的应用也比较广泛 [15] [16] ，但对于闭频繁项集本身理论的研究比较少。我们对其理论进行了仔细梳理，发现还有很多细节值得深思和理解。本文主要以顾客购买商品的场景来理解闭频繁项集的概念、性质及相关结论等，给出相应的定理及证明，对闭频繁项集的理论框架有更深入的剖析，并配合实例进行了演示，希望对闭频繁项集的理论发展起到比较深入的促进作用。

2. 闭频繁项集相关定义、定理

令 $I=\left\{x_1,x_2,\cdots ,x_m\right\}$ 为一组称作项(item)的元素的集合。集合 $X\subseteq I$ 称为项集(itemset)。I可以表示超市中售卖的所有商品的集合、一个网站所有页面的集合等。一个基数大小为k的项集称为k项集。我们用 $I^{\left(k\right)}$ 表示所有k项集的集合，即所有大小为k的、I的子集 [10] 。

令 $T=\left\{t_1,t_2,\cdots ,t_n\right\}$ 为另一个由所谓的事务标识符(tid)构成的集合 [10] 。集合 $\ddot{T}\subseteq T$ 称为一个事务标识符集。我们假设项集和事务标识符集都是按照字母顺序排列的。T可以表示购买商品的顾客集合。

一个二元数据库D表示了事务标识符集合和项集之间的二元关系 [10] ，即 $D\subseteq T\times I$ 。我们说事务标识符 $t\in T$ 包含项 $x\in X$ ，当且仅当 $\left(t,x\right)\in D$ 。这里的 $\left(t,x\right)\in D$ ，在商品购买过程中，可以表示顾客t购买了商品x。

下面，为了给出闭频繁项集的定义，先给出两个相关函数的定义 [10] [17] ：

定义1. 函数 $t:2^I\to 2^T$ ，定义为 $t\left(X\right)=\left\{t\in T|t包含x\right\}$ ，其中 $X\subseteq I$ ，且t(X)是包含项集X中所有项的事务标识符集合。

定义2. 函数 $i:2^T\to 2^I$ ，定义为 $i\left(\ddot{T}\right)=\left\{x|\forall t\in \ddot{T},t包含x\right\}$ ，其中 $\ddot{T}\subseteq T$ ，且i(T)是事务标识符集T中所有事务的公共项集的集合。具体地说，i(t)是事务标识符 $t\in T$ 中包含的项的集合。

例1 [10] . 商品A、B、C、D、E被6个顾客购买的情况如下，第一个表格是6个顾客购买情况的二进制表示，其中0表示没购买、1表示购买了某个商品；第二个表格是6个事务标识符对应商品情况，即6个顾客的事务标识符是 $t_{\text{1}},t_{\text{2}},\cdots ,t_{\text{6}}$ ，其中

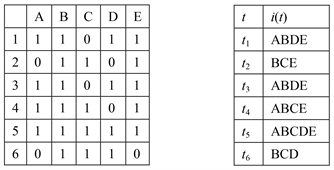
每位顾客的购买情况分别表示为

$i\left(t_{\text{1}}\right)=\left\{\text{ABDE}\right\},i\left(t_{\text{2}}\right)=\left\{\text{BCE}\right\},\cdots ,i\left(t_{\text{6}}\right)=\left\{\text{BCD}\right\}$

顾客们购买物品的交叉情况如

$i\left(t_{\text{1}},t_{\text{2}}\right)=\left\{\text{BE}\right\},i\left(t_{\text{1}},t_{\text{2}},t_{\text{3}}\right)=\left\{\text{BE}\right\},i\left\{t_{\text{1}},t_{\text{2}},t_{\text{3}},t_{\text{4}},t_{\text{5}}\right\}=\left\{\text{BE}\right\},i\left(t_{\text{1}},t_{\text{2}},t_{\text{3}},t_{\text{4}},t_{\text{5}},t_{\text{6}}\right)=\left\{\text{B}\right\}.$

单件商品被顾客购买的情况：

$\begin{array}{l}t\left(\text{A}\right)=\left\{t_{\text{1}}{t}_{\text{3}},t_{\text{4}},t_{\text{5}}\right\},t\left(\text{B}\right)=\left\{t_{\text{1}},t_{\text{2}},t_{\text{3}},t_{\text{4}},t_{\text{5}},t_{\text{6}}\right\},t\left(\text{C}\right)=\left\{t_{\text{2}},t_{\text{4}},t_{\text{5}},t_{\text{6}}\right\},\\ t\left(\text{D}\right)=\left\{t_{\text{1}},t_{\text{3}},t_{\text{5}},t_{\text{6}}\right\},t\left(\text{E}\right)=\left\{t_{\text{1}},t_{\text{2}},t_{\text{3}},t_{\text{4}},t_{\text{5}}\right\};\end{array}$

多件商品共同一起被顾客购买的情况：

$t\left(\text{AB}\right)=\left\{t_{\text{1}},t_{\text{3}},t_{\text{4}},t_{\text{5}}\right\},t\left(\text{AC}\right)=\left\{t_{\text{4}},t_{\text{5}}\right\},\cdots ,t\left(\text{ABC}\right)=\left\{t_{\text{4}},t_{\text{5}}\right\},\cdots ,t\left(\text{ABCDE}\right)=\left\{t_{\text{5}}\right\}.$

这里讨论一下函数t和i的单调性，在文献 [17] 中提出来这样的性质，但并没有给出相关证明，我们针对顾客购买商品的情况下进行了如下证明。

定理1. 如果 $X_k\subseteq X_q$ ，则 $t\left(X_q\right)\subseteq t\left(X_k\right)$ ，即t是单调减函数；如果 $T_k\subseteq T_q$ ，则 $i\left(T_q\right)\subseteq i\left(T_k\right)$ ，即i是单调减函数。

证明：(1) $t\left(X_k\right)$ 和 $t\left(X_q\right)$ 分别表示共同购买了商品集合 $X_k$ 和 $X_q$ 的事务集合，而 $X_k\subseteq X_q$ ，则共同购买了 $X_q$ 的顾客不会比共同购买的 $X_k$ 多，因为购买了 $X_q$ 的顾客必然购买了 $X_k$ ，所以有 $t\left(X_q\right)\subseteq t\left(X_k\right)$ 。说明函数t是单调减的。

(2) $i\left(T_k\right)$ 表示事务集 $T_k$ 里共同购买过的商品集合， $i\left(T_q\right)$ 表示事务集 $T_q$ 里共同购买过的商品集合，而 $T_k\subseteq T_q$ ，说明 $T_q$ 集合里除了有 $T_k$ 的事务集之外还有更多的事务标识符，则能从 $T_q$ 里找到的共同商品集合不会多于从 $T_k$ 里找到的共同商品集合，所以有 $i\left(T_q\right)\subseteq i\left(T_k\right)$ ，即i函数的单调减的。

关于上面单调性定理，举例如下面例2。

例2. 根据例1的商品购买情况，我们假设X₁ = {B}，X₂={AB}，则有

$t\left(X_{\text{1}}\right)=t\left(\text{B}\right)=\left\{t_{\text{1}},t_{\text{2}},t_{\text{3}},t_{\text{4}},t_{\text{5}},t_{\text{6}}\right\}$ ，而 $t\left(X_{\text{2}}\right)=t\left(\text{AB}\right)=\left\{t_{\text{1}},t_{\text{3}},t_{\text{4}},t_{\text{5}}\right\}$ ，可见 $t\left(\text{AB}\right)\subseteq t\left(\text{B}\right)$ ；假设 $i\left\{t_{\text{1}},t_{\text{2}},t_{\text{3}}\right\}=\left\{\text{BE}\right\}$ ，而 $i\left\{t_{\text{1}},t_{\text{2}},t_{\text{3}},t_{\text{4}},t_{\text{5}},t_{\text{6}}\right\}=\left\{\text{B}\right\}$ ，有 $i\left\{t_{\text{1}},t_{\text{2}},t_{\text{3}},t_{\text{4}},t_{\text{5}},t_{\text{6}}\right\}\subseteq i\left\{t_{\text{1}},t_{\text{2}},t_{\text{3}}\right\}$ 。

为了方便起见，没有严格使用集合的表示，例如：我们用i(t)表示i({t})，用i(t₁t₂)表示i({t₁,t₂}))，用t(A)表示t({A})，用t(AB)表示t({A,B})等。

定义3. 项集X的支持度为 [10] ： $\sup \left(X\right)=\left|\left\{t|\left(t,x\right)\in D\right\}\right|$ ，也就是商品集合X被购买的次数，或者说是商品集合X被购买的顾客数。

定义4. 闭包算子(closure operator)为c： $2^I\to 2^I$ ，定义如下 [10] ：

$c\left(X\right)=i\circ t\left(X\right)=i\left(t\left(X\right)\right)$ ,

且c(X)称为X的闭包。

关于闭包算子的举例如下面例3。

例3. 根据例1求几个项集的闭包，

(1) $c\left(\text{AB}\right)=i\circ t\left(\text{AB}\right)=i\left(t\left(\text{AB}\right)\right)$ ，这里 $t\left(\text{AB}\right)=\left\{t_{\text{1}},t_{\text{3}},t_{\text{4}},t_{\text{5}}\right\}$ ，所以

$i\left(t\left(\text{AB}\right)\right)=i\left(\{t_1,t_3,t_4,t_5\}\right)=i\left(t_1,t_3,t_4,t_5\right)=\left\{\text{ABE}\right\}$ ,

于是，{ABE}是{AB}的闭包。

(2) $c(\text{CD})=i\circ t\left(\text{CD}\right)=i\left(t\left(\text{CD}\right)\right)$ ，这里 $t\left(\text{CD}\right)=\left\{t_{\text{5}},t_{\text{6}}\right\}$ ，所以

$i\left(t\left(\text{CD}\right)\right)=i\left(\left\{t_{\text{5}},t_{\text{6}}\right\}\right)=i\left(t_{\text{5}},t_{\text{6}}\right)=\left\{\text{BCD}\right\}$ ,

于是，{BCD}称为{CD}的闭包。

(3) $c\left(\text{BD}\right)=i\circ t\left(\text{BD}\right)=i\left(t\left(\text{BD}\right)\right)$ ，这里 $t\left(\text{BD}\right)=\left\{t_{\text{1}},t_{\text{3}},t_{\text{5}},t_{\text{6}}\right\}$ ，所以

$i\left(t\left(\text{BD}\right)\right)=i\left(\left\{t_{\text{1}},t_{\text{3}},t_{\text{5}},t_{\text{6}}\right\}\right)=i\left(t_{\text{1}},t_{\text{3}},t_{\text{5}},t_{\text{6}}\right)=\left\{\text{BD}\right\}$ ,

于是，{BD}是自己的闭包。

(4) $c\left(\text{ABD}\right)=i\circ t\left(\text{ABD}\right)=i\left(t\left(\text{ABD}\right)\right)$ ，这里 $t\left(\text{ABD}\right)=\left\{t_{\text{1}},t_{\text{3}},t_{\text{5}}\right\}$ ，所以

$i\left(t\left(\text{ABD}\right)\right)=i\left(t_1,t_3,t_5\right)=\left\{\text{ABDE}\right\}$ .

于是，{ABDE}是{ABD}的闭包。

理解1：闭包，就是定义2和3中t函数和i函数复合作用的结果，其过程相当于先根据商品找到它们的共同购买者，然后再看这些共同购买者购买的项数最多的共同商品集合，也就是说，闭包运算是一个从商品集合到商品集合的一个映射过程。

定理2. c(X)是X的闭包，则 $\sup \left(c\left(X\right)\right)=\sup \left(X\right)$ 。

证明： $c\left(X\right)=i\left(t\left(X\right)\right)$ ，则 $\sup \left(c\left(X\right)\right)=\sup \left(i\left(t\left(X\right)\right)\right)$ ，分解理解1，t(X)是购买商品集合X的顾客集合，而i(t(X))是顾客集合t(X)共同购买的最大商品集合，寻找闭包的这个过程中，顾客集合t(X)没有改变，这群顾客既购买了X商品集合，也是购买了i(t(X))这个商品集合，所以 $\sup \left(i\left(t\left(X\right)\right)\right)=\sup \left(X\right)$ ，所以 $\sup \left(c\left(X\right)\right)=\sup \left(X\right)$ 。

关于闭包算子的如下定理3的性质，格论的文献里给的闭包算子本身就用这3条特性进行定义的 [18] ，当然就没有给出相关证明。我们在这里沿着文献 [17] 给出的闭包算子的定义，然后证明该算子在商品购买的情景中满足这三条特性。文献 [10] 里也有这三条性质，但没有给出证明，我们这里利用前面的定理1和定理2来给出这三条性质的证明。

定理3. 闭包算子c将项集映射到项集，且满足如下3个特性 [10] ：

(1) 递增性(extensive)： $X\subseteq c\left(X\right)$ ；

(2) 单调性(monotonic)：若 $X_i\subseteq X_j$ ，则 $c\left(X_i\right)\subseteq c\left(X_j\right)$ ；

(3) 幂等性(idempotent)： $c\left(c\left(X\right)\right)=c\left(X\right)$ 。

证明：

(1) 假设从商品集X₁出发，共同购买了商品集X₁的事务集合有 $t_{i1},t_{i2},\cdots ,t_{ik}$ ，则 $t_{i1},t_{i2},\cdots ,t_{ik}$ 至少共同购买了商品集X₁，或者还共同购买了除X₁之外的其他商品，所以 $X\subseteq c\left(X\right)$ 。

(2) 设 $X_i\subseteq X_j$ ，根据定理1，有 $t\left(X_j\right)\subseteq t\left(X_i\right)$ ，表明事务集 $t\left(X_j\right)$ 更小且又包含在事务集 $t\left(X_i\right)$ 中，再根据定理1，就有 $i\left(t\left(X_i\right)\right)\subseteq i\left(t\left(X_j\right)\right)$ ，从而得到

$c\left(X_i\right)=i\circ t\left(X_i\right)=i\left(t\left(X_i\right)\right)\subseteq i\left(t\left(X_j\right)\right)=i\circ t\left(X_j\right)=c\left(X_j\right)$ .

(3) t(X)是寻找购买过X的顾客，t(c(X))是共同购买过c(X)的顾客，而c(X)是X的闭包、二者具有相同的顾客群，所以 $t\left(c\left(X\right)\right)=t\left(X\right)$ ，所以 $i\left(t\left(c\left(X\right)\right)\right)=i\left(t\left(X\right)\right)$ 。

定义5 [10] . 若项集X满足 $c\left(X\right)=X$ ，则称其为封闭的(closed)，即X是闭包算子c的一个定点，即X被称为封闭项集。另一方面，若 $c\left(X\right)\ne X$ ，则X是不封闭的，集合c(X)称为X的闭包。

理解2：每一个频繁项集X，其闭包一定存在。

这是因为，根据理解1，对于一个被购买频繁的商品集合X，一定能找到共同购买过X的顾客集合T，再反过来查找这群顾客集合T共同购买过的最大商品集合Z，那么这个商品集合Z就是X的闭包，这个过程一定能做到，所以X的闭包一定存在。

关于一个商品集合是否封闭，举例如下面例4。

例4. 比如上面例3(1)中 $c\left(\text{AB}\right)=\left\{\text{ABE}\right\}\ne \left\{\text{AB}\right\}$ ，这说明{ABE}是{AB}的闭包；而例2(3)中c(BD) = {BD}，这说明{BD}是封闭的。

根据闭包算子的性质，可以知道X和c(X)有相同的事务标识符集. 由此可知，若频繁集 $X\in F$ (F是所有频繁项集的集合)没有与之频率相同的频繁超集，则它是封闭的；因为根据定义，它是事务标识符集t(X)中所有事务标识符的最大公共项集。

定理4. 如果Z是X的闭包，则有 $\sup \left(X\right)=\sup \left(Z\right)$ 。

证明：如果X是封闭的，则有c(X)=X，当然就有 $\sup \left(X\right)=\sup \left(Z\right)$ ；如果X不是封闭的，则根据理解2关于寻找c(X)的过程知道，购买X和购买c(X)的是同一群顾客，即它们对应的事务标识符集合T是一样的，而T中的顾客数正是X和c(X)的支持度，所以有 $\sup \left(X\right)=\sup \left(Z\right)$ 。

定义6 [10] . 所有闭频繁项集的集合定义如下：

$C=\left\{X|X\in F且不存在Y\supset X,使得\sup \left(X\right)=\sup \left(Y\right)\right\}$ .

换句话说，X是封闭的，若X的所有超集的支撑度更小，即对于所有的 $Y\supset X$ ，都有 $\text{sup}\left(X\right)>\text{sup}\left(Y\right)$ 。

定理5. 若存在一个闭频繁项集 $Z\in C$ 使得项集X满足 $X\subseteq Z$ ，则X是频繁的。更进一步，X的支持度为 $\sup \left(X\right)=\max \left\{\sup \left(Z\right)|Z\in C,X\subseteq Z\right\}$ [10] 。

证明：

首先，因为 $X\subseteq Z$ ，所以有 $\sup \left(X\right)\ge \sup \left(Z\right)$ 。

其次，设X的闭包为某个Z，即，根据定理4，有 $\sup \left(X\right)=\sup \left(Z\right)$ 。

综上，有 $\sup \left(X\right)=\max \left\{\sup \left(Z\right)|Z\in C,X\subseteq Z\right\}$ 。

上面的定理5在文献 [10] 中有相应描述，但并没有给出标准的证明过程。

理解3：根据上面定理，如果X是闭频繁项集，则其超集支持度严格比它的小；如果X不是闭频繁项集，则存在其超集Z，使得 $\sup \left(Z\right)=\sup \left(X\right)$ ，且这样的超集Z就是X闭包。

定理6. 对于频繁项集X，设 $S=\left\{Z|Z\supseteq X且\sup \left(Z\right)=\sup \left(X\right)\right\}$ ，S里最大(项数最多)那个超集Z_m，就是X的闭包。

证明：根据 $S=\left\{Z|Z\supseteq X且\sup \left(Z\right)=\sup \left(X\right)\right\}$ ，因为 $\sup \left(Z\right)=\sup \left(X\right)$ ，说明购买超集商品集Z的顾客群和购买商品集X的顾客群是一样的，即 $t\left(Z\right)=t\left(X\right)$ 。而根据理解1，X的闭包就顾客集合t(X)或者t(Z)购买的最大商品集合 $Z_m\in S$ ，而这个最大商品集合Z_m也是该顾客群购买的，即 $t\left(Z_m\right)=t\left(Z\right)=t\left(X\right)$ ，所以Z_m是X的闭包。

理解4：根据定理6，可以把支持度相等的集合归为一个等价类 $S=\left\{Z|Z\supseteq X且\sup \left(Z\right)=\sup \left(X\right)\right\}$ ，其中，使得 $\left|Z_m\right|=\max \left(\left\{\left|Z\right|,Z\in S\right\}\right)$ 的Z_m是该等价类中所有项集的闭包。

理解5：根据定理6和定理3(1)，同一个等价类里，类代表“闭包”这个项集包含了该类所有的其他项集。

定理7：频繁项集X的闭包是所有包含X的闭频繁项集中最小(项数最少)的。

证明：

设 $Z^{\prime }=\left\{Z|Z\supseteq X,且不存在Y\supset Z使得\sup \left(Y\right)=\sup \left(Z\right)\right\}$ ，那么X的闭包c(X)就在Z'里面，假设Z中有闭项集Z₁， $Z_1\supseteq X$ ，使得 $\left|c\left(X\right)\right|>\left|Z_1\right|$ ，出现下面两种情况：

(1) 如果 $c\left(X\right)\supseteq Z_1$ ，

则 $\sup \left(c\left(X\right)\right)\le \sup \left(Z_1\right)$ ，又因为Z₁是闭项集，所以不存在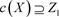使得 $\sup \left(c\left(X\right)\right)=\sup \left(Z_1\right)$ ，所以有 $\sup \left(c\left(X\right)\right)<\sup \left(Z_1\right)$ ，说明c(X)和Z₁不在一个等价类，则Z₁不能是等价类的闭包，Z₁不可能是X的闭包。

(2) 如果 $c\left(X\right)⊉Z_1$ ，根据理解5，说明Z₁和c(X)不在同一个等价类，则Z₁不能是等价类的闭包，Z₁不可能是X的闭包。这里还不对。

综上，不存在闭项集Z₁， $Z_1\supseteq X$ ，使得 $\left|c\left(X\right)\right|>\left|Z_1\right|$ ；说明，凡是有这样的闭项集Z₁， $Z_1\supseteq X$ ，就有 $\left|c\left(X\right)\right|\le \left|Z_1\right|$ ，证毕。

注意：上面提到的项集的最大和最小，是指其包含项数的最多或者最少。

综合以上定义、定理及理解，得到如下结论：

一个二元数据库D上所有闭频繁项集的集合C是该数据库的一种紧凑表示，其中的每个闭频繁项集X是所有和它支持度相等、以它为闭包的商品集合的代表。

根据例1的商品购买数据库D，可以得到图1表示的情形，其中，每个矩形小方块里面是一个频繁项集和其对应的事务标识符集合，比如商品A被顾客集合{1,2,4,5}里每个顾客都购买了；每个带阴影的小方块里的项集是闭频繁项集；以某个闭频繁项集为闭包的商品项集被划分到同一个不规则圈里，可以看成一类，该类的项集具有相同的支持度。比如这4个商品集合{A、AB、AE、ABE}所在的圈内，ABE是闭频繁项集，其它三个商品集合都以它为闭包，ABE就是该类的代表，这4个频繁项集具有相同的支持度，即 $\text{sup}\left(\text{A}\right)=\text{sup}\left(\text{AB}\right)=\text{sup}\left(\text{AE}\right)=\text{sup}\left(\text{ABE}\right)$ 。该图是文献 [10] 的第9章的图9-2的一部分，我们主要关注图里的一般频繁项集、闭频繁项集以及它们相应的等价类划分，比文献 [10] 里关注和表达的主题少，这里主要是用来验证我们关于闭频繁项集的结论。

Figure 1. Schematic diagram of the closed itemset and equivalence classes for the goods purchase in Example 1

图1. 例1的商品购买情况的闭项集和等价类分别示意图

3. 结论

挖掘闭频繁项集，是关联规则分析中挖掘频繁项集的一种紧凑和简洁的挖掘方式，并因此挖掘到感兴趣的关联规则。本文对闭频繁项集的定义和细节进行了梳理，其中对于闭包定义中的函数t和i进行了单调性证明；对闭包算子定义满足的性质进行了证明；对频繁项集和其闭包、以及它们的超集的支持度之间的关系进行了分析和证明，反过来根据支持度和项集之间的包含情况进行了项集的闭包的确定并给出了相应结论，从而进行了等项集等价类的划分。整个论文在购物篮关联规则分析的情景中对闭频繁项集的理论进行了透彻的分析和探究，相对于目前众多研究者们只注重挖掘闭频繁项集的算法来说，我们反过来，对其本身的理论进行探讨、从底层进行分析，希望在闭频繁项集的理论方面更进一步探索到有意义的细节，然后再促进相应挖掘算法的进展，这也是我们未来一个阶段研究思路。

基金项目

全国统计科学研究重大项目(2021LD01)。

参考文献

NOTES

^*共同第一作者。