1. 引言
随机微分方程是一个历史悠久的研究学科,1902年,Gibbs [1] 在统计力学研究中首次提出了随机微分方程问题。它可以用来模拟控制理论、生物学、经济学、物理学、电气工程和机械中的许多现实世界现象。在这些模型中,我们可以有效地描述随机扰动对系统状态时间演化的影响。因此,随机微分方程理论发展非常迅速,并且越来越完善。对于随机微分方程的系统知识,读者可以参见 [2] [3] [4] [5] 和参考文献。
现实现象的一个显著特征是不确定性,不确定性可以从随机性和模糊性两个方面来解释。研究者发现,现实生活中的某些系统会因为实验设备和观测等不可抗拒的因素而产生误差,导致变量、数据和参数模糊,信息不完整。由于信息是不精确的,这种不精确需要反映在模型结构中。因此,提出了模糊集理论 [6] [7] [8] 和模糊随机微分方程来处理这些不确定性。在文献 [9] - [16] 中,我们可以找到许多关于模糊随机微分方程的研究,它适用于建模随机性和模糊性相结合的动力系统。然而,在由“白噪声”起作用的系统里,模糊随机微分方程将是对不确定性现象建模的最佳方法。这方面的论文较少,即 [10] [17] [18] [19] [20] [21] ,每篇论文在考虑模糊随机微分方程的方式或条件设置上都有所不同。
迄今为止,关于模糊分数阶随机微分方程的研究成果很少。然而,在初值问题中,系统解的存在唯一性定理是一个重要的课题。在文献 [22] [23] 中,研究者利用逐次逼近的思想,在广义Hukuhara可微性下,得到了随机模糊分数阶微分方程解的存在唯一性定理。不同的是Riemann-Liouville分数阶导数的研究文献有 [23] ,而Caputo型分数阶导数的研究文献有 [22] 。在文献 [24] [25] 中,研究者使用Mazandarani等人 [26] 提出的颗粒导数代替了传统的Hukuhara可微性和收缩原理。分别得到了模糊分数阶随机受电弓延迟微分系统和脉冲模糊分数阶随机微分系统的存在唯一性。关于模糊分数阶随机微分方程的其他结果,请参考文献 [27] [28] [29] 。
基于先前的讨论,本文探究下面具有时滞的模糊分数阶随机微分方程的存在性、唯一性:
这里
是Caputo导数,区间
,阶数
,函数
、
是连续函数,
。历史函数
满足关系
,其中
表示数学期望,h代表时滞,
,
的含义在第2节可以找到。
本文结构安排:在第2节中,我们将介绍文中的符号和必需的定义、引理.第3节致力于证明模糊分数阶随机微分方程解的存在性和唯一性.最后,为了清楚地解释结果,在第4节中提供一个说明性示例。
2. 预备知识
在本节,我们将介绍文中的符号和一些有用定义,引理。这些有用的工具将用于建立主要结果。
符号:设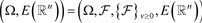 是一个带有滤子
完备概率空间且满足通常的条件,
是定义在概率空间
上的m-维布朗运动。让
表示所有强可测平方可积
值随机变量。
是一个带有滤子
完备概率空间且满足通常的条件,
是定义在概率空间
上的m-维布朗运动。让
表示所有强可测平方可积
值随机变量。
对于
,
表示从
到
所有连续映射且满足
,显然,
是一个Banach空间。设
是
中所有连续过程Z构成的有界闭子空间,
由
-适应可测过程
组成且度量为:
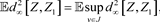
容易验证
与上述度量构成一个完备的度量空间
。
定义2.1 [25] 设
表示
中的所有非空、紧和凸子集族,则两个非空集合
之间的Hausdorff距离
定义如下:
这里
代表
中的标准Euclidean范数。
是完备的度量空间且度量
有下面的性质:
对所有的
和
,有
1)
,
2)
,
3)
。
定义2.2 [24] 记
:
(i)
是正规的模糊集,即存在
,有
,
(ii)
是上半连续的,
(iii)
,其中cl表示闭包,
(iv)
是模糊凸的,即对所有的
和
,有
(v)
,
则称
为模糊数,称
为模糊数空间,显然
。集合
能够嵌入
通过如下的嵌入映射
:对于所有的
定义2.3 [25] 如
,则集合
,
,
被称为
的
-水平集。
符号
代表
的
-水平集,这里
,
分别表示
的左、右两支。对于
和
,模糊数的加法和标量乘法定义为:
和
定义2.4 [24] 令
,则它们之间的Hausdorff距离定义如下:
,
其中
和
。模糊数空间
是一个不可分的完备度量空间。
对于
,
和
,此外,
的直径
。
命题2.5 [30] 若
,
,
,我们有下面的性质:
1)
,
2)
,
3)
,
4)
,
5)
,
,
其中
。
定义2.6 [30] 若
,如果存在
使得
,则称u为
的Hukuhara差,记作
。
根据命题2.5和定义2.6,我们不难得到下面的引理。
引理2.7:对任意的
,有
1)
,
2)
。
定义2.8 [31] 一个函数
在区间
被称为d-递减(d-递增),如果对任意的
,函数
在区间
上是非增的(非减的)。此外,如果
在区间
是d-递减或者d-递增,我们称
在
是d-单调。
定义2.9 [31]
的广义Hukuhara差(gH-差)定义为:
定义2.10 [32] 设
,
阶模糊Riemann-Liouville积分定义为:
这里
是伽马函数,
和
。
定义2.11 [31] 设
是一个模糊值函数使得Riemann-Liouville导数
在
存在,此时,
阶Caputo模糊分数阶导数定义为:
注意到如果
是一个d-单调的模糊值函数,有
此外
引理2.12 [19] 设
,其中
,则对任意的
,有
引理2.13 [19] 设
,则对任意的
,有
定义2.14:一个模糊随机过程
被称为(1)的解当它满足下面的条件:
(i)
是
-连续和
-适应。
(ii)
在区间
上d-递增和一个d-单调的模糊函数
,它满足:
(2)
其中
,
(iii) 对于任何其他解
,我们有
。
引理2.15:对任意的
,设
在区间
是一个d-单调函数:
(i) 如果
是d-递增函数,那么(2)式等价于:
(ii) 如果
是d-递减函数,那么(2)式等价于:
证明:对于情况(i),根据
在区间
上是一个d-递增函数,这暗示
,通过定义2.9(i),我们得到情况(i)的结果。
对于情况(ii),根据
在区间
上是一个d-递减函数,这暗示
,通过定义2.9(ii),有
再利用定义2.6,便得到想要的结果。值得一提是,情况(ii)的积分形式是本文讨论的重点。
3. 主要结果
在本节,我们假设系统(1)的解
是一个d-递减函数,除此之外,我们要求积分
在区间
是d-递增的。然后,我们探索系统(1)解的性质是利用Banach不动点定理。根据定义2.14和引理2.15,我们知道
满足:
(3)
为了建立本文的结论,我们作如下假设:
(H1) 假设这儿存在一个连续非减的实值函数
和
,使得对每个
和所有的
,有
这里f和g是可测的连续函数,
和
定义为
。
(H2) 对于
,存在一个常数
,使得
定理3.1:若假设条件(H1)和(H2)成立,那么方程(1)在
中有唯一解,前提是
其中
。
证明:对每个正数q,定义
。然后对每个q,显然
是
里面的有界闭凸集,定义算子
如下:
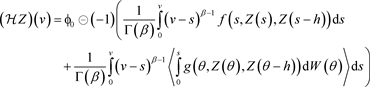
步骤1:接下来证明存在常数q,使得
。
现在,利用引理2.12,对
进行估计:
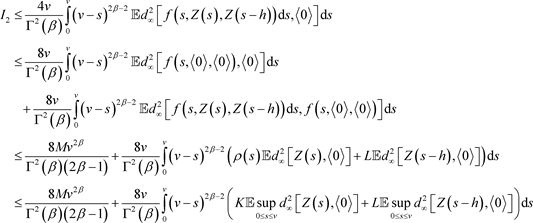
借助引理2.13和积分中值定理,我们对
进行估计:
综上,我们有
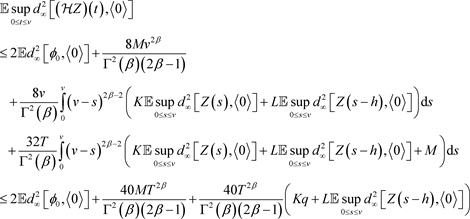
又
是介于q与
之间。所以
因此,我们得到
。
步骤2:推导
是一个压缩映射。
假设
,
和当
时,有
。对每个
,我们考虑:
当
,
时,根据文献 [30] 中定理3.1,我们得到
因此
根据压缩映射原理,我们知道算子
有唯一的不动点
是方程(1)的解。这是定理3.1的完整证明。
4. 例子
在本节,提出一个例子来说明我们的主要结果。
考虑下面一维模糊分数阶随机微分方程:
(4)
这里
,
,记
.
我们指出
是一个d-递减函数(见图1);F在区间
上是d-递增的(见图2)。这是因为
类似的推导,我们有
因此,我得到
所以条件(H1)~(H2)满足,而且
故方程(4)有唯一解。
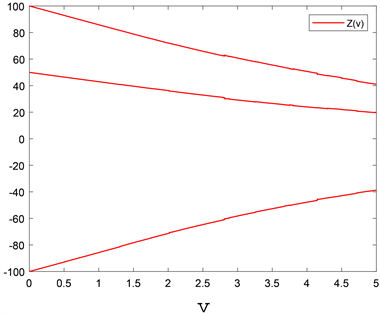
Figure 1. The solution
of Equation (4)
图1. 方程(4)中的解

Figure 2. The shape of F in Equation (4)
图2. 方程(4)中的F的形状
5. 总结与展望
本文通过利用Banach不动点定理与随机分析技术,得到了一类Caputo型模糊分数阶随机微分方程解的存在唯一性。并给出一个数值算例验证理论结果的有效性。本文的结果对模糊分数阶随机系统解的稳定性研究有一定借鉴作用。在下一步的工作中,我们将考虑其他类型的模糊分数阶随机系统解的存在性以及脉冲效应对系统的影响。
基金项目
本论文得到了国家自然科学基金(No. 12061018)的资助。
参考文献
NOTES
*通讯作者。