CAE_AD：基于卷积自编码器的无监督时间序列异常检测方法

CAE_AD: Unsupervised Time Series Anomaly Detection Method Based on Convolutional Autoencoder

摘要: 时间序列数据的有效异常检测对现代工业应用非常重要。然而，由于缺乏异常标签、数据高波动性、训练不稳定，导致建立一个能够准确地进行异常检测的系统是一个具有挑战性的问题。尽管异常检测的深度学习方法最近有所发展，但其中只有少数能够应对所有这些挑战。本文提出了CAE_AD，这是一种基于卷积自编码器(CAE)的无监督异常检测模型。为了尽量地放大异常，避免错过异常，笔者引入了两阶段的对抗训练。同时，为了提高训练稳定性，笔者引入了第一阶段的重建误差以作为第二阶段卷积自编码器的输入。笔者将CAE_AD与先进的时间序列异常检测方法在多个数据集上进行了比较。实验结果表明，本文提出的模型性能优于这些对比方法。在SMAP数据集上，相比于其他模型，CAE_AD模型的f1领先了4%，Precision领先了8%。

Abstract: Effective anomaly detection of time series data is crucial for modern industrial applications. How-ever, due to the lack of anomaly labels, high data volatility, and unstable training, establishing a system that can accurately detect anomalies is a challenging problem. Although deep learning methods for anomaly detection have recently developed, only a few of them can address all of these challenges. This article proposes CAE_AD, which is an unsupervised anomaly detection model based on convolutional autoencoder (CAE). In order to maximize the amplification of anomalies and avoid missing them, the author introduced two-stage adversarial training. Meanwhile, in order to improve training stability, the author introduced the reconstruction error from the first stage as the input for the convolutional autoencoder in the second stage. The author compared CAE_AD with advanced time series anomaly detection methods on multiple data sets. The experimental results show that the model proposed in this article performs better than these comparison methods. On the SMAP dataset, compared to other models, the CAE_AD model has a 4% lead in f1 and an 8% lead in Precision.

1. 引言

近几十年来，异常检测一直是机器学习领域的核心研究之一，具有广泛的应用。异常检测似乎是一个简单的两类分类，即可以利于对正常或异常数据进行分类。然而，它也面临着以下挑战。

首先，训练数据正负样本高度不平衡。因为与正常数据相比，数据集中的异常数据通常非常罕见。其次，用户没有简单的方法来手动标记每个训练数据，特别是异常标签。由于上述挑战，与半监督和监督学习方法相比，使用无监督学习方法进行异常检测的趋势越来越大，因为无监督方法可以处理不平衡和未标记的数据。

另外，工业场景中，物联网平台中的传感器和设备数量不断增加，同时数据具有高的波动性，导致异常检测模型的训练稳定性越来越差。

现有解决方案。上述挑战导致开发了无数用于自动异常检测的无监督学习解决方案。研究人员开发了基于重建的方法，其主要目的是封装时间趋势，并以无监督的方式重建时间序列数据，然后使用重建数据与真实数据的差值作为异常分数。传统方法，如基于密度的时间序列异常检测方法LOF [1] 、COF [2] ，基于聚类的时间序列异常检测方法DBSCAN [3] 、CBLOF [4] ，基于距离的时间序列异常检测方法KNN [5] 、K-means [6] ，基于树的时间序列异常检测方法iForest [7] 、决策树 [8] 。基于循环神经网络RNN [9] 的方法可以捕捉时间戳之间的依赖关系，但是训练RNN需要花费大量的时间，效率低。MAD_GAN [10] 使用生成对抗网络(GAN)进行异常检测，但是训练GAN会存在不收敛的问题。LSTM-NDT [11] 方法使用基于长短期记忆网络(LSTM)来预测数据，并使用输入时间序列和非参数动态阈值方法来检测预测误差中的异常，然而LSTM模型在面临高波动性的数据时会出现不稳定性和梯度消失现象。

针对生成对抗网络GAN训练时不收敛、不稳定的问题，笔者设计了基于卷积自编码器CAE的无监督时间序列异常检测方法CAE_AD，该方法受到生成对抗网络(GAN)的启发，基于卷积自编码器架构。CAE_AD基于编码器–解码器架构的对抗性训练，使用重建误差使其能够学习如何放大微弱异常。本文的主要贡献如下：

(1) 提出了基于卷积自编码器(CAE)的无监督时间序列异常检测模型，以解决实际应用中异常标签少、正负样本不均衡的问题。

(2) 如果重建误差太小，即重建值相对接近正常数据，卷积自编码器(CAE)往往会错过异常。将卷积自编码器(CAE)和对抗训练相结合，可以放大重建偏差，避免错过微弱的异常。

(3) 将第一阶段的重建误差作为第二阶段的输入，可以提高模型的训练稳定性，以解决数据高波动性导致训练不稳定的问题。

2. 相关工作

时间序列异常检测问题在学术界和工业界研究已久，关于时间序列异常检测的方法有很多，包括基于密度、聚类、距离、树等传统的异常检测方法。近年来，基于深度学习的时间序列异常检测方法日益成为研究的重点，LSTM_NDT [11] 、OmniAnomaly [12] 、DAGMM [13] 、MAD_GAN [10] 、USAD [14] 是近年来性能比较好的深度学习异常检测方法，本文以这五个模型作为实验对比模型。LSTM_NDT模型 [11] 使用长短期记忆网络(LSTM)模型来预测输入数据下一个时间戳的数据，并且提出了一种非参数异常阈值方法NDT，然而LSTM模型在面临高波动性的数据时会出现不稳定性和梯度消失现象。OmniAnomaly [12] 是一种用于多变量时间序列异常检测的随机递归神经网络，其核心思想是利用随机变量连接和平面归一化流等关键技术，通过学习多变量时间序列的鲁棒表示，捕捉多变量时间系列的正态模式，通过表示重构输入数据，并利用重构概率确定异常。DAGMM [13] 是一种用于无监督异常检测的深度自编码高斯混合模型，为每个输入数据点生成低维表示和重建误差，并将其进一步输入到高斯混合模型。DAGMM以端到端的方式同时联合优化深度自动编码器和混合模型的参数，利用单独的估计网络来促进混合模型的参数学习，然而DAGMM很慢，并且不能很好地利用模态间的相关性。MAD_GAN [10] 是一种基于生成对抗网络(GAN)的无监督多变量异常检测方法，使用长短期记忆递归神经网络(LSTM-RNN)作为GAN框架中的基本模型(即生成器和鉴别器)来捕获时间序列分布的时间相关性，使用一种称为DR评分的新异常评分来通过判别和重建来检测异常，但是训练GAN会存在不收敛的问题。USAD [14] 使用两个自编码器通过对抗性训练来实现异常检测，其自动编码器架构使其能够以无监督的方式进行学习，对抗性训练及其体系结构的使用使其能够在提供快速训练的同时隔离异常，然而在训练高波动性的数据时存在训练不稳定的问题。

针对以上方法存在容易错过微弱异常、训练不收敛和训练不稳定的问题，笔者设计了基于卷积自编码器CAE的无监督时间序列异常检测方法CAE_AD。针对存在容易错过微弱异常的问题，笔者将卷积自编码器和两阶段的对抗训练相结合，放大第一阶段的重建误差，避免错过微弱的异常；针对MAD_GAN和USAD训练过程中的不收敛和不稳定问题，笔者将第一阶段的重建误差作为第二阶段的输入，提高模型的训练稳定性，以解决数据高波动性导致训练不稳定的问题。最后，在公共数据集上的实验对比分析表明了所提模型的有效性。

3. 基于卷积自编码器的无监督异常检测方法

本节中，将从时间序列异常检测的问题描述、数据处理、两阶段的对抗训练、异常分数的计算方法四个方面来介绍基于卷积自编码器的无监督异常检测方法。

3.1. 时间序列异常检测的问题描述

在时间序列异常检测中，数据通常是带有时间戳的长度为T的一系列数据点

$T=\left\{x_1,\mathrm{...},x_T\right\}$ (1)

其中，每一个数据点 $x_t$ 在特定的时间戳t被物理传感器采集， $x_t\in R^m$ 。如果m > 1，此时为多变量时间序列数据；如果m = 1，是一种特殊情况，此时是单变量时间序列数据。在本文中，我们考虑使用无监督的方法做时间序列异常检测。训练时，给定训练输入时间序列T，假设T只包含正常数据，无异常数据。测试时，对于长度为 $\hat{L}$ 的测试数据 $\hat{T}$ ，我们重建 $\hat{T}$ 得到模型的输出O，如果测试数据 $\hat{T}$ 与模型输出O的差值大于阈值D，则检测为异常值。通过上述方法，我们得到检测结果 $Y=\left\{y_1,\mathrm{...},y_{\hat{L}}\right\}$ ，使用 $y_t\in \left\{0,1\right\}$ 来表示测试集的时间戳t数据是否为异常值。 $y_t$ 为1表示为异常数据点，此时测试数据 $\widehat{T_t}$ 与模型输出 $O_t$ 的差值大于等于阈值D； $y_t$ 为0表示为正常数据点，此时测试数据 $\widehat{T_t}$ 与模型输出 $O_t$ 的差值小于阈值D。

3.2. 数据处理

为了提高模型的收敛速度，防止模型梯度爆炸，使用线性归一化方法对数据进行了归一化操作。线性归一化方法的公式如下

$x_t\leftarrow \frac{x_t-\min \left(T\right)}{\max \left(T\right)-\min \left(T\right)}$ (2)

其中， $\min \left(T\right)$ 是训练数据中的最小向量值， $\max \left(T\right)$ 是训练数据中的最大向量值。经过过一化后，全部数据处于[0, 1]范围内。为了捕捉时间戳之间的依赖关系，提高模型的准确性，将某个时间戳的数据扩大到包含这个时间戳的一段区间。对于时间戳t，定义长度为K的时间窗口 $W_t$ ：

$W_t=\left\{x_{t-K+1},\mathrm{...},x_{t-1},x_t\right\}$ (3)

如果t < K，使用长度为K − t的向量 $\left\{x_t,\mathrm{...},x_t\right\}$ 追加填充在 $W_t$ 的尾部，以维持 $W_t$ 的长度为K。定义滑动窗口序列W作为模型训练的输入数据，W定义如下：

$W=\left\{W_1,\mathrm{...}{W}_T\right\}$ (4)

在测试时，使用 $\hat{W}$ (长度为 $\hat{L}$ )作为测试的输入数据，通过本文提出的模型，得到重建值O。在t时间，使用输入数据 $\widehat{W_t}$ 和重建值 $O_t$ 来计算异常分数 $S_t$ ，如果异常分数 $S_t$ 大于阈值D，则检测结果 $y_t=1$ (检测为异常)，否则检测结果 $y_t=0$ (检测为正常)。

3.3. 两阶段的对抗训练

本文中的CAE_AD模型基于两阶段对抗训练的卷积自编码器(CAE)架构，如图1所示。CAE_AD由三个部分组成：一个编码器网络Encoder和两个解码器网络Decoder1和Decoder2。如图2所示，有两个卷积自编码器CAE1和CAE2，共享编码器网络Encoder。CAE_AD分为两个阶段进行训练。首先，训练两个CAE来完成对输入窗口W的重建。然后，CAE1和CAE2进行对抗式的训练，其中CAE1尽可能地生成与真实数据W接近的数据来试图欺骗CAE2，而CAE2的目标是学习数据是真实的(直接来自W)还是重构生成的(来自CAE1)。

Figure 1. CAE_AD model diagram

图1. CAE_AD模型图

第一阶段：卷积自编码器训练。在第一阶段，目的是训练CAE1和CAE2学习重建输入窗口W。输入窗口W被编码器Encoder压缩到潜在变量Z，然后由解码器Decoder1和Decoder2将潜在变量Z还原到和输入窗口W一样的维度，从而得到重建值 $O_1$ 和 $O_2$ 。这个过程可由如下公式表示：

$O_1=D_1\left(E\left(W\right)\right)$ (5)

$O_2=D_2\left(E\left(W\right)\right)$ (6)

在第一阶段，使用L2范数定义两个解码器的重建损失，如下：

$L_1={\Vert O_1-W\Vert }_2$ (7)

$L_2={\Vert O_2-W\Vert }_2$ (8)

第二阶段：两阶段对抗性训练。目的是训练CAE2区分真实数据和来自CAE1的重建数据，训练 CAE1欺骗CAE2。使用 ${\Vert O_1-W\Vert }_2$ 来作为第一阶段的重建误差。在第二阶段，使用第一阶段的重建误差作为第二阶段的输入，重建误差被编码器Encoder压缩到潜在空间 $Z$ ，然后被Decoder2重建得到 $\widehat{O_2}$ 。第二阶段的重建值 $\widehat{O_2}$ 可由如下公式表示：

$\widehat{O_2}=D_2\left(E\left({\Vert O_1-W\Vert }_2\right)\right)$ (9)

在对抗训练中，CAE1目的是最小化第二阶段重建输出 $\widehat{O_2}$ 和输入窗口 $W$ 之间的差异，通过完美地重建输入(即 $O_1$ 约等于 $W$ ，相差很小)来创建一个重建误差 ${\Vert O_1-W\Vert }_2$ ，从而欺骗CAE2。而CAE2的目的是最大限度地扩大第二阶段重建输出 $\widehat{O_2}$ 和输入窗口 $W$ 之间的差异。训练CAE1是否成功欺骗了CAE2，训练CAE2是否可以将CAE1的重建数据 $O_1$ 与真实数据 $W$ 区分开来。训练目标是

$\underset{CAE1}{\min }\underset{CAE2}{\max }{\Vert \widehat{O_2}-W\Vert }_2$ (10)

CAE1的目标是使 ${\Vert \widehat{O_2}-W\Vert }_2$ 最小化，而CAE2的目标是使 ${\Vert \widehat{O_2}-W\Vert }_2$ 最大化。通过使用损失来实现：

$L_1=+{\Vert \widehat{O_2}-W\Vert }_2$ (11)

$L_2=-{\Vert \widehat{O_2}-W\Vert }_2$ (12)

现在有了第一阶段的重建损失和第二阶段的对抗性损失，可以得到CAE1和CAE2的两阶段累计损失函数。具体的损失函数如下：

$L_1=\frac{1}{n}{\Vert O_1-W\Vert }_2+\left(1-\frac{1}{n}\right){\Vert \widehat{O_2}-W\Vert }_2$ (13)

$L_2=\frac{1}{n}{\Vert O_2-W\Vert }_2-\left(1-\frac{1}{n}\right){\Vert \widehat{O_2}-W\Vert }_2$ (14)

n表示当前训练的轮次，从1开始递增。在训练的初始阶段，n比较小，1/n比较大，(1 − 1/n)比较小。即刚开始训练时，让重建损失的权重很高，对抗性损失的权重很低，目的是保证第一阶段重建效果不佳时(第一阶段的重建值 $O_1$ 和输入窗口 $W$ 的值相差较大)的训练稳定性。在第一阶段重建不佳的情况下，那么作为第二阶段输入的重建误差 ${\Vert O_1-W\Vert }_2$ 将不可靠。因此，在训练的初始阶段，对抗性损失被赋予较低的权重，以防止出现训练不稳定的问题。随着训练的轮数n不断增加，第一阶段的重建值 $O_1$ 越来越接近输入窗口 $W$ ，使得重建误差 ${\Vert O_1-W\Vert }_2$ 越来越准确，对抗性损失的权重也在增加。

3.4. 异常分数的计算方法

在异常检测的测试阶段，对于测试集输入数据 $\hat{W}$ ，异常分数被定义为

$S=\mu {\Vert O_1-\hat{W}\Vert }_2+\eta {\Vert \widehat{O_2}-\hat{W}\Vert }_2$ (15)

其中 $\mu +\eta =1$ ，可以动态调整异常分数中的第一阶段和第二阶段的权重，使得模型对两个阶段的灵敏度不同，以适应不同的应用场景。

在测试阶段，如果异常分数大于阈值，则标记当前时间戳t为异常值。使用POT [15] 方法来自动和动态地选择阈值，POT使用“极值理论”将数据分布与广义帕累托分布拟合，并确定适当的风险值，以动态确定阈值。

数据的维度是m，每个维度的异常诊断标签 $y_i$ 和检测结果 $y$ 定义为

$y_i=1\left(S_i\ge POT\left(S_i\right)\right)$ (16)

$y=\underset{i}{\vee }{y}_i$ (17)

只要m维中任意一个维度为异常的，那么就将当前时间戳标记为异常。

4. 实验结果和分析

本节中，在4.1中介绍了实验用到的三个公开数据集，在4.2中介绍了实验用到的评价指标，在4.3中分析了CAE_AD模型中四个参数对实验结果的影响，在4.4中CAE_AD使用4.3中得到的性能最优的四个参数，与MAD_GAN、LSTM_NDT、DAGMM、OmniAnomaly、USAD模型进行了性能对比，在4.5中对CAE_AD模型进行了消融实验。

4.1. 公开数据集

在实验中，使用了3个公开的数据集：SMAP、SWaT、MSL。在表1中总结了3个数据集的基本情况，包括训练集、测试集的大小，维度，异常率，括号中的值是数据集中的实体数。比如，MSL数据集有27个实体，每个实体有55个维度。下面详细介绍上述3个数据集的情况。

Table 1. Dataset situation

表1. 数据集情况

土壤水分监测卫星时序数据集(SMAP)和火星科学实验室探测器“好奇号”时序数据集(MSL)是美国国家航天航空局NASA的卫星公开时序数据集。SMAP数据集有55个实体，每个实体包含25个维度，整体异常率为13.13%；MSL数据集有27个实体，每个实体包含55个维度，整体异常率为10.72%。

安全水处理(SWaT)数据集源自于新加坡公用事业委员会协调的运行水处理试验台。数据收集了持续四天的51个传感器记录，频率为1秒。总共进行了36次攻击，导致11.98%的时间出现了异常状况。因此，SWaT数据集有一个实体，这个实体包含51个维度，整体异常率有11.98%。

4.2. 评价指标

在介绍用于评估时间序列异常检测性能的指标之前，首先介绍4个符号：TP (真阳性)、FP (假阳性)、FN (假阴性)、TN (真阴性)。TP是所有被正确预测为正的样例数；FP是所有被错误预测为正的样例数；TN是所有被正确预测为负的样例数；FN是所有被错误预测为负的样例数。

用于评估时间序列异常检测性能的指标有精确率Precision (P)，召回率Recall (R)，和F1score (F1)。

(1) 精确率(查准率)：所有被正确预测为正的样例占所有被预测为正的样例的比重。

$P=\frac{\text{TP}}{\text{TP}+\text{FP}}$ (18)

(2) 召回率(查全率)：所有被正确预测为正的样例占所有实际为正的样例的比重。

$R=\frac{\text{TP}}{\text{TP}+\text{FN}}$ (19)

(3) F1：精确率P和召回率R的调和均值。简单来说，F1越大，precision和recall的值越大，即F1越大越好。

$F1=2\cdot \frac{P\cdot R}{P+R}$ (20)

4.3. 参数影响

本节中，为使CAE_AD模型尽可能地取得最优的性能，将分析CAE_AD模型中四个重要参数对实验结果的影响。接下来，将从滑动窗口大小、编码器输出通道数、卷积核大小、异常分数参数四个方面来分别分析其对实验结果的影响。

4.3.1. 滑动窗口大小

滑动窗口的大小K在重建时间序列数据，以及在判断异常结果时发挥着重要的作用。同时，窗口大小K定义了输入数据W的长度，可以直接影响异常检测的速度。图2显示了CAE_AD模型使用不同的窗口大小在SMAP数据集上取得的异常检测性能结果，K取[10, 25, 50, 75, 100]。如果滑动窗口的大小K过小，则不能很好地反映时间序列数据在时间维度的特征；如果滑动窗口的大小K过大，则会导致异常检测模型在大时间跨度对时间序列数据建模缺乏敏感性，以及导致模型重建的难度大大增加，同时大大降低了异常检测的速度。因此，对于SMAP数据集，一个长度适中的窗口大小更利于CAE_AD模型发挥出最优的异常检测性能。由图2可知，当窗口大小K等于25时，异常检测的性能最优，取得了最好的F1、AUC、Precision指标效果。

Figure 2. The effect of sliding window size on experimental performance

图2. 滑动窗口大小对实验性能的影响

4.3.2. 编码器输出通道数

接下来，研究编码器中最后一个卷积层的输出通道数Z。卷积核的通道数是卷积操作中的一个重要参数，可以影响异常检测模型的性能和计算速度。合理地选择卷积核通道数，可以让卷积操作更有效，提高异常检测模型的表征能力。

图3显示了CAE_AD模型使用不同的输出通道数Z在SMAP数据集上取得的异常检测性能结果，Z取[16, 32, 64, 128, 256]。通过增加卷积核通道数可以扩大卷积核在特征空间的搜索范围，从而能够更好地捕捉时间序列数据的局部特征，以提高异常检测模型的表征能力。如果卷积核通道数Z过小，那么卷积输出的特征可能无法包含数据的全部信息，导致模型出现欠拟合的现象；如果卷积核通道数Z过大，则模型可能会出现过拟合的现象。因此，编码器中最后一个卷积层输出通道数Z的选择需要在欠拟合和过拟合之间寻求一个平衡点，以达到最优的异常检测性能。由图3可知，输出通道数Z等于32时，CAE_AD模型异常检测的性能最优。

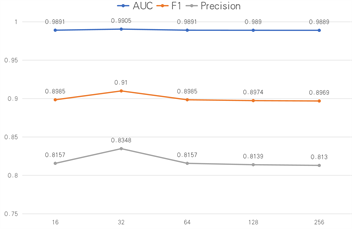
Figure 3. The influence of encoder output channel number on experimental performance

图3. 编码器输出通道数对实验性能的影响

4.3.3. 卷积核大小

卷积层中的卷积核大小对异常检测模型的检测性能非常重要。图4显示了CAE_AD模型使用不同的卷积核大小在SMAP数据集上取得的异常检测性能结果，卷积核大小取[(2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7), (8, 8), (9, 9)]。增加卷积核的大小可以让模型有更大的感受野，有利于进行特征提取。如果卷积核过大，会使整个模型的复杂度急剧增加；如果卷积核过小，又会使训练的速度降低。因此，选择大小合适的卷积核对异常检测的性能非常重要。由图4可知，卷积核大小等于(3, 3)时，CAE_AD模型异常检测的性能最优。

Figure 4. The effect of convolutional kernel size on experimental performance

图4. 卷积核大小对实验性能的影响

4.3.4. 异常分数的参数

最后，研究了异常分数中的两个参数(µ, η)对异常检测性能的影响。如果µ大于η，则说明模型更注重第一阶段的重建；如果µ小于η，则说明模型更注重第二阶段的重建。可以动态地调整(µ, η)，以改变模型对第一阶段和第二阶段的重视程度，进而使CAE_AD模型具有不同的灵敏度，以适应不同生产环境的要求。

图5显示了CAE_AD模型使用不同的(µ, η)在SMAP数据集上取得的异常检测性能结果，(µ, η)取[(0.0, 1.0), (0.1, 0.9), (0.2, 0.8), (0.3, 0.7), (0.4, 0.6), (0.5, 0.5), (0.6, 0.4), (0.7, 0.3), (0.8, 0.2), (0.9, 0.1), (1.0, 0.0)]。使用不同的(µ, η)，可以使CAE_AD模型实现不同级别的灵敏度，提高了异常检测的灵活性。由图5可知，当(µ, η)等于(0.3, 0.7)时，CAE_AD模型异常检测的性能最优。

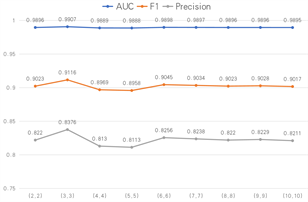
Figure 5. The effect of anomalous score parameters on experimental performance

图5. 异常分数参数对实验性能的影响

4.4. 对比实验结果

本节中，使用4.3中得到的最优参数，滑动窗口大小为25，编码器输出通道数为32，卷积核大小为(3, 3)，异常分数参数(µ, η)为(0.3, 0.7)，将CAE_AD模型与MAD_GAN、LSTM_NDT、DAGMM、OmniAnomaly、USAD等模型在SMAP、SWaT、MSL数据集上进行了性能对比。

Table 2. Performance comparison of six models on SMAP, SWaT, and MSL datasets

表2. 六种模型在SMAP、SWaT、MSL数据集上的性能对比

表2详细说明了在公开数据集上所有时间序列异常检测方法取得的性能结果。在F1指标上，CAE_AD模型的表现在三个公开数据集上优于所有对比的方法，尤其在SMAP数据集上，CAE_AD模型的F1是94.09%，比对比方法中效果最好的USAD模型(F1是89.47%)提高了4.6%。在召回率R和AUC这两个指标上，CAE_AD在三个公开数据集上同样取得了最好的成绩，优于对比的5个异常检测方法。在精确率P指标上，在SMAP和MSL数据集上CAE_AD模型优于其他对比方法；在SWaT数据集上，LSTM_AD的精确率P最高(99.99%)，CAE_AD精确率P是97.39%。

4.5. 消融实验

为了研究CAE_AD模型中每个部分对于异常检测结果的影响，设计CAE_AD模型的三种消融变体，以进一步说明CAE、重建误差、对抗性训练在异常检测中起到的重要作用。

第一个变体CAE_AD_1：相对于CAE_AD模型，将CΑΕ中的卷积模块换成了线性层，以研究CAE中卷积模块对异常检测结果的影响。

第二个变体CAE_AD_2：相对于CAE_AD模型，删除了第一阶段的重建误差，而使用第一阶段的输出O1作为第二阶段的输入，以研究重建误差模块对异常检测结果的影响。

第三个变体CAE_AD_3：相对于CAE_AD模型，删除了对抗性训练，即使用第一阶段的重建误差进行单一阶段的推理，以研究对抗训练对异常检测结果的影响。

实验结果如表3所示，在SMAP数据集上三个消融变体和CAE_AD的对比效果最为明显。

Table 3. Ablation Research: Performance comparison of CAE_AD and its ablation variants

表3. 消融实验：CAE_AD及其消融变体的性能对比

以下结论以SMAP数据集上的效果为根据：

(1) 就F1指标而言，第三个变体CAE_AD_3的性能下降最快，大约4.5%，这表明对抗性训练对于异常检测结果的作用非常关键。如果重建偏差太小，即相对接近正常数据，模型往往会错过异常，对抗性训练可以放大重建偏差，以缓解上述问题。

(2) 当使用第二个变体CAE_AD_2，即删除重建误差后，F1指标性能下降了大约2.5%，这表明重建误差可以显著提高第二阶段的重建性能。将第一阶段的重建残值作为第二阶段的输入，可以提高模型的训练稳定性，以解决数据高波动性导致训练不稳定的问题。

(3) 当第一个变体CAE_AD_1，即将CAE中的卷积模块换成线性模块，F1指标下降了4.24%，这表明卷积模块对异常检测的结果非常重要。

总之，CAE_AD模型中任何模块的消融都会导致较差的结果。

5. 结束语

在本文中，提出了基于卷积自编码器(CAE)的无监督时间序列异常检测方法CAE_AD。CAE_AD模型使用卷积自编码器来实现对输入数据的重建，通过无监督异常检测的方式解决实际应用中异常标签少、正负样本不均衡的问题。CAE_AD模型通过两阶段的对抗训练来放大第一阶段的重建误差，避免错过微小的异常。此外，CAE_AD模型将第一阶段的重建误差作为第二阶段的输入，从而提高模型的训练稳定性，以解决数据高波动性导致训练不稳定的问题。在实验研究中，CAE_AD模型在三个公共数据集上表现出优秀的性能，相对于对比方法，F1分数领先了4%，Precision领先了8%。CAE_AD模型为在高维数据或者高波动性数据上进行无监督异常检测提供了一个有希望的方向。