一类花图f(C_m,F_n)的Tutte多项式

The Tutte Polynomials of a Class of Flower Graph f(C_m,F_n)

摘要: 图多项式不变量已被证实在量子化学和生物信息方面有重要的应用。著名的图多项式不变量之一是Tutte多项式，它包含了关于图结构的各种有趣的信息。本文借助Tutte多项式的一些性质对一类花图f(C_m,F_n)进行研究，最终得到这类花图Tutte多项式的具体表达式。

Abstract: Polynomial graph invariants have been confirmed to have important applications in quantum chemistry and biological information. One of the famous polynomial graph invariants is the Tutte polynomial which gives multifarious interesting information about the graph structure. In this pa-per, with the help of some properties of Tutte polynomials, a class of flower diagrams f(C_m,F_n) is studied, and finally the specific expressions of Tutte polynomials of this kind of flower diagrams are obtained.

1. 引言

Tutte多项式是空间图多项式不变量的一个重要代表，Tutte多项式 [1] 是色多项式的推广，它是由Tutte在1954年提出的，并且由Tutte多项式可以得到色多项式、流多项式、可靠性多项式等图的多项式不变量 [2] 。Tutte多项式包含图的大量信息，由Tutte多项式可以得到图的生成树数目、连通生成子图数目等 [3] ，从而研究一个图的Tutte多项式是极为重要的。近年来，国内外学者提出了许多关于Tutte多项式的研究课题。2013年，Brennan利用生成函数的方法计算出扇图的Tutte多项式 [4] 。2016年，Chen H和Deng H利用生成子图定义计算得到几类无标度网络图的Tutte多项式 [5] 。2019年，Chen H和Guo Q利用Tutte多项式的删除–收缩性质计算出交错多边形链的的具体表达式 [6] 。2021年，徐得卿等学者主要利用转移矩阵的方法求解了两类六角系统的Tutte多项式 [7] 。近几年，许多学者对花图这类图形展开了大量的研究。花图 $f\left(C_3,F_n\right)$ 是在2015年由I. S. Kumala和A. N. M. Salman所定义，并研究了这类花图的彩虹连接数 [8] ；2020年，Pranata P Y等学者将花图 $f\left(C_3,F_n\right)$ 中的循环图 $C_3$ 推广到 $C_m$ ，研究并确定了花图 $f\left(C_m,F_n\right)$ 的星数确切值 [9] 。

本文主要研究一类花图 $f\left(C_m,F_n\right)$ 的Tutte多项式，共分为两部分，第一部分介绍相关的基础知识，在第二部分，借助Tutte多项式的性质计算得到花图 $f\left(C_m,F_n\right)$ 的Tutte多项式。

2. 预备知识

2.1. 图

图G定义为一个偶对 $\left(V,E\right)$ ，记作 $G=\left(V,E\right)$ ，其中：

1) V是一个有限的非空集合，其元素称为顶点或点，用 $V\left(G\right)$ 表示顶点集合；

2) E是无序积 $V\times V$ 中的一个子集合，其元素称为边，且集合 $V\times V$ 中的元素在E中可以重复出现多次，用 $E\left(G\right)$ 表示边的集合。

3) 一条边x，y被称为连接顶点x和y，用xy表示；顶点x和y是这条边的末端顶点。如果 $xy\in E\left(G\right)$ ，那么x和y是G的相邻顶点，并且顶点x和y与边xy相伴。如果两条边正好有一个共同的端点，那么它们就是相邻的 [10] 。

2.2. Tutte多项式

图G的Tutte多项式 [11] $T\left(G;x,y\right)$ 可以定义为：

$T\left(G;x,y\right)=\{\begin{array}{l}\text{1}若E\left(G\right)=\phi \hfill \\ xT\left(G/e;x,y\right)若e是割边\hfill \\ yT\left(G-e;x,y\right)若e是环\hfill \\ T\left(G-e;x,y\right)+T\left(G/e;x,y\right)若e既不是割边也不是环\hfill \end{array}$

其中 $G-e$ 和 $G/e$ 分别表示图G删除边e和收缩边e后得到的图。

性质1：设 $G\cup G^{\prime }$ 是G和 $G^{\prime }$ 的不交并， $G\ast G^{\prime }$ 是 $G\cap G^{\prime }$ 当且仅当为一个顶点，则有：

$T\left(G\cup G^{\prime }\right)=T\left(G\right)T(\; G\; \prime \; )$

$T\left(G\ast G^{\prime }\right)=T\left(G\right)T(\; G\; \prime \; )$

性质2：长为n的循环图 $C_n$ 的Tutte多项式为：

$T\left(C_n;x,y\right)={\displaystyle \underset{i=1}{\overset{n-1}{\sum }}{x}^i}+y$

3. 花图 $f\left(C_m,F_n\right)$ 的Tutte多项式

定义3.1 设 $C_m$ 是一个有m个点的循环图， $F_n=P_n+\left\{x\right\}$ ，其中 $P_n=v_1,v_2,\cdots ,v_n$ 是一条有n个顶点的路径，x与 $v_i$ 相邻， $\forall i\in \left[1,n\right]$ 。花图 $f\left(C_m,F_n\right)$ 是通过在 $C_m$ 的每条边接枝 $\left(v_1,x\right)\in E\left(F_n\right)$ 而形成的图，将花图 $\left(C_m,F_n\right)$ 记作 $f\left(C_m,F_n\right)$ [9] 。花图 $f\left(C_m,F_n\right)$ 如图1所示。

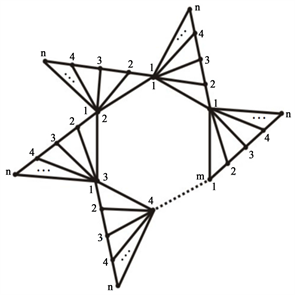
Figure 1. Flower graph $f\left(C_m,F_n\right)$

图1. 花图 $f\left(C_m,F_n\right)$

计算花图 $f\left(C_m,F_n\right)$ 的Tutte多项式

定理3.1 花图 $f\left(C_m,F_n\right)$ 的Tutte多项式为：

$\begin{array}{c}T\left(f\left(C_m,F_n\right);x,y\right)=\frac{\left[y{r}_1-yT\left(F_n;x,y\right)+By\right]T\left(F_{n-1}^{+};x,y\right)+2AT\left(F_n;x,y\right)}{r_1\left(B+T\left(F_n;x,y\right)+r\right)}{\left(\frac{B+T\left(F_n;x,y\right)+r_1}{2}\right)}^n\\ +\frac{\left[y{r}_1+yT\left(F_n;x,y\right)-By\right]T\left(F_{n-1}^{+};x,y\right)-2AT\left(F_n;x,y\right)}{r_1\left(B+T\left(F_n;x,y\right)-r\right)}{\left(\frac{B+T\left(F_n;x,y\right)-r_1}{2}\right)}^n\end{array}$

其中：

$\begin{array}{c}A=\frac{\left(1+x^2+y-r+xr-xy\right)\left(x+y+1+r\right)}{\text{2}xr\left(1-x-y-r\right)}\left[1-{\left(\frac{x+y+1+r}{\text{2}}\right)}^{n-1}\right]\\ -\frac{\left(1+x^2+y+r-xr-xy\right)\left(x+y+1+r\right)}{\text{2}xr\left(1-x-y+r\right)}\left[1-{\left(\frac{x+y+1-r}{2}\right)}^{n-1}\right]-y+1\end{array}$

$\begin{array}{c}B=\frac{\left(y+x^2+x-x{y}^2+y^{2}r+yr+xr-y^3\right)}{r\left(1-x-y-r\right)}\left[\text{1}-{\left(\frac{x+y+1+r}{2}\right)}^{n-1}\right]\\ -\frac{\left(y+x^2+x-x{y}^2-y^{2}r-yr-xr-y^3\right)}{r\left(1-x-y+r\right)}\left[\text{1}-{\left(\frac{x+y+1-r}{2}\right)}^{n-1}\right]-y^2+1\end{array}$

$T\left(F_n;x,y\right)=\left(\frac{1+x^2+y-r+xr-xy}{\text{2}xr}\right){\left(\frac{x+y+1+r}{2}\right)}^n-\left(\frac{1+x^2+y+r-xr-xy}{\text{2}xr}\right){\left(\frac{x+y+1-r}{2}\right)}^n$

$\begin{array}{c}T\left(F_n^{+};x,y\right)=\frac{y+x^2+x-x{y}^2+y^{2}r+yr+xr-y^3}{r\left(x+y+1+r\right)}{\left(\frac{x+y+1+r}{2}\right)}^n\\ -\frac{y+x^2+x-x{y}^2-y^{2}r-yr-xr-y^3}{r\left(x+y+1-r\right)}{\left(\frac{x+y+1-r}{2}\right)}^n\end{array}$

$r=\sqrt{{\left(x+y+1\right)}^2-4xy}$ ； $r_{\text{1}}=\sqrt{{\left[B+T\left(F_n;x,y\right)\right]}^2-4BT\left(F_n;x,y\right)}$ 。

证明：根据Tutte多项式的删除–收缩性质可得：

$T\left(f\left(C_m,F_n\right);x,y\right)=T($ $)+T$

$=T($ $)+T($ $)T(\; )$

$=T($ $)+T\left(F_{n-1}^{+};x,y\right)T\left(f\left(C_{m-1},F_n\right);x,y\right)$

$=T\left(F_{n-1};x,y\right){\left[T\left(F_n;x,y\right)\right]}^{m-1}+T($ $)+T\left(F_{n-1}^{+};x,y\right)T\left(f\left(C_{m-1},F_n\right);x,y\right)$

$=T\left(F_{n-1};x,y\right){\left[T\left(F_n;x,y\right)\right]}^{m-1}+T($ $)+\left[T\left(F_{n-1}^{+};x,y\right)+T\left(F_{n-2}^{+};x,y\right)\right]T\left(f\left(C_{m-1},F_n\right);x,y\right)$

$=\left[T\left(F_{n-1};x,y\right)+T\left(F_{n-\text{2}};x,y\right)\right]{\left[T\left(F_n;x,y\right)\right]}^{m-1}+T(\; )$

$+\left[T\left(F_{n-1}^{+};x,y\right)+T\left(F_{n-\text{2}}^{+};x,y\right)\right]T\left(f\left(C_{m-1},F_n\right);x,y\right)$

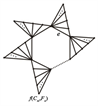
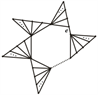
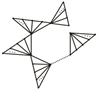
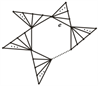
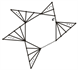
一直这样作下去得到：

$=\left[T\left(F_{n-1};x,y\right)+\cdots +T\left(F_{\text{2}};x,y\right)+x\right]{\left[T\left(F_n;x,y\right)\right]}^{m-1}+T(\; )$

$+\left[T\left(F_{n-1}^{+};x,y\right)+\cdots +T\left(F_2^{+};x,y\right)+x+y\right]T\left(f\left(C_{m-1},F_n\right);x,y\right)$

$=\left[T\left(F_{n-1};x,y\right)+\cdots +T\left(F_{\text{2}};x,y\right)+x+1\right]{\left[T\left(F_n;x,y\right)\right]}^{m-1}+[T\left(F_{n-1}^{+};x,y\right)+\cdots$

$+T\left(F_2^{+};x,y\right)+x+y+\text{1}]T\left(f\left(C_{m-1},F_n\right);x,y\right)$

设：

$A=T\left(F_{n-1};x,y\right)+\cdots +T\left(F_{\text{2}};x,y\right)+x+1$

$B=T\left(F_{n-1}^{+};x,y\right)+\cdots +T\left(F_2^{+};x,y\right)+x+y+1$

已知 [12] $T\left(F_n;x,y\right)=\left(\frac{1+x^2+y-r+xr-xy}{\text{2}xr}\right){\left(\frac{x+y+1+r}{2}\right)}^n-\left(\frac{1+x^2+y+r-xr-xy}{\text{2}xr}\right){\left(\frac{x+y+1-r}{2}\right)}^n$

其中 $r=\sqrt{{\left(x+y+1\right)}^2-4xy}$

那么就有：

$\begin{array}{l}T\left(F_{n-1};x,y\right)+\cdots +T\left(F_{\text{2}};x,y\right)+T\left(F_{\text{1}};x,y\right)\\ =\frac{\left(1+x^2+y-r+xr-xy\right)\left(x+y+1+r\right)}{\text{2}xr\left(1-x-y-r\right)}\left[1-{\left(\frac{x+y+1+r}{2}\right)}^{n-1}\right]\\ -\frac{\left(1+x^2+y+r-xr-xy\right)\left(x+y+1-r\right)}{\text{2}xr\left(1-x-y+r\right)}\left[1-{\left(\frac{x+y+1-r}{2}\right)}^{n-1}\right]\end{array}$

$\begin{array}{c}A=\frac{\left(1+x^2+y-r+xr-xy\right)\left(x+y+1+r\right)}{\text{2}xr\left(1-x-y-r\right)}\left[1-{\left(\frac{x+y+1+r}{\text{2}}\right)}^{n-1}\right]\\ -\frac{\left(1+x^2+y+r-xr-xy\right)\left(x+y+1+r\right)}{\text{2}xr\left(1-x-y+r\right)}\left[1-{\left(\frac{x+y+1-r}{2}\right)}^{n-1}\right]-y+1\end{array}$

接下来计算 $F_n^{+}$ 的Tutte多项式。

$T\left(F_n^{+};x,y\right)=T(\; )$

$=xT\left(F_{n-1}^{+};x,y\right)+T(\; )$

$=\left(x+y+1\right)T\left(F_{n-1}^{+};x,y\right)-xyT\left(F_{n-2}^{+};x,y\right)$

于是： $T\left(F_n^{+};x,y\right)=\left(x+y+1\right)T\left(F_{n-1}^{+};x,y\right)-xyT\left(F_{n-2}^{+};x,y\right)$ ，这是一个具有恒定系数的2阶线性递归关系，从中我们可以得到一个特征多项式：

${\lambda }^2-\left(x+y+1\right)\lambda +xy=0$

那么， ${\lambda }_{\text{1}}$ 和 ${\lambda }_{\text{2}}=\frac{x+y+1\pm r}{\text{2}}$ ， $r=\sqrt{{\left(x+y+1\right)}^2-4xy}$

解下列方程组：

$\{\begin{array}{l}T\left(F_1^{+};x,y\right)=a_1\left(\frac{x+y+1+r}{2}\right)+a_2\left(\frac{x+y+1-r}{2}\right)\\ T\left(F_2^{+};x,y\right)=a_1{\left(\frac{x+y+1+r}{2}\right)}^2+a_2{\left(\frac{x+y+1-r}{2}\right)}^2\end{array}$

其中： $T\left(F_1^{+};x,y\right)=y^2+y+x$ ， $T\left(F_2^{+};x,y\right)=y^2+y+x^2+x+xy$

解得：

$\{\begin{array}{l}{a}_1=\frac{y+x^2+x-x{y}^2+y^{2}r+yr+xr-y^3}{r\left(x+y+1+r\right)}\\ a_2=\frac{y+x^2+x-x{y}^2-y^{2}r-yr-xr-y^3}{-r\left(x+y+1-r\right)}\end{array}$

那么， $F_n^{+}$ 的Tutte多项式就为：

$\begin{array}{c}T\left(F_n^{+};x,y\right)=\frac{y+x^2+x-x{y}^2+y^{2}r+yr+xr-y^3}{r\left(x+y+1+r\right)}{\left(\frac{x+y+1+r}{2}\right)}^n\\ -\frac{y+x^2+x-x{y}^2-y^{2}r-yr-xr-y^3}{r\left(x+y+1-r\right)}{\left(\frac{x+y+1-r}{2}\right)}^n\end{array}$

其中 $r=\sqrt{{\left(x+y+1\right)}^2-4xy}$

于是，就有：

$\begin{array}{l}T\left(F_{n-1}^{+};x,y\right)+\cdots +T\left(F_2^{+};x,y\right)+T\left(F_1^{+};x,y\right)\\ =\frac{\left(y+x^2+x-x{y}^2+y^{2}r+yr+xr-y^3\right)}{r\left(1-x-y-r\right)}\left[\text{1}-{\left(\frac{x+y+1+r}{2}\right)}^{n-1}\right]\\ -\frac{\left(y+x^2+x-x{y}^2-y^{2}r-yr-xr-y^3\right)}{r\left(1-x-y+r\right)}\left[\text{1}-{\left(\frac{x+y+1-r}{2}\right)}^{n-1}\right]\end{array}$

则：

$\begin{array}{c}B=T\left(F_{n-1}^{+};x,y\right)+\cdots +T\left(F_2^{+};x,y\right)+x+y+1\\ =T\left(F_{n-1}^{+};x,y\right)+\cdots +T\left(F_2^{+};x,y\right)+T\left(F_1^{+};x,y\right)-T\left(F_1^{+};x,y\right)+x+y+1\\ =\frac{\left(y+x^2+x-x{y}^2+y^{2}r+yr+xr-y^3\right)}{r\left(1-x-y-r\right)}\left[\text{1}-{\left(\frac{x+y+1+r}{2}\right)}^{n-1}\right]\\ -\frac{\left(y+x^2+x-x{y}^2-y^{2}r-yr-xr-y^3\right)}{r\left(1-x-y+r\right)}\left[\text{1}-{\left(\frac{x+y+1-r}{2}\right)}^{n-1}\right]-y^2+1\end{array}$

由上可知：

$T\left(f\left(C_m,F_n\right);x,y\right)=A{\left[T\left(F_n;x,y\right)\right]}^{m-1}+BT\left(f\left(C_{m-1},F_n\right);x,y\right)$

那么就有：

$T\left(f\left(C_{m-1},F_n\right);x,y\right)=A{\left[T\left(F_n;x,y\right)\right]}^{m-2}+BT\left(f\left(C_{m-2},F_n\right);x,y\right)$

所以：

$T\left(f\left(C_m,F_n\right);x,y\right)=\left[B+T\left(F_n;x,y\right)\right]T\left(f\left(C_{m-1},F_n\right);x,y\right)-BT\left(F_n;x,y\right)T\left(f\left(C_{m-2},F_n\right);x,y\right)$

从中我们可以得到一个特征多项式：

${\lambda }^2-\left[B+T\left(F_n;x,y\right)\right]\lambda +BT\left(F_n;x,y\right)=0$

解得：

${\lambda }_{\text{1}}$ 和 ${\lambda }_{\text{2}}=\frac{B+T\left(F_n;x,y\right)\pm r}{\text{2}}$

其中 $r_{\text{1}}=\sqrt{{\left[B+T\left(F_n;x,y\right)\right]}^2-4BT\left(F_n;x,y\right)}$

解下列方程组：

$\{\begin{array}{l}T\left(f\left(C_1,F_n\right);x,y\right)=a_1\left[\frac{B+T\left(F_n;x,y\right)+r_1}{2}\right]+a_2\left[\frac{B+T\left(F_n;x,y\right)-r_1}{2}\right]\\ T\left(f\left(C_1,F_n\right);x,y\right)=a_1{\left[\frac{B+T\left(F_n;x,y\right)+r_1}{2}\right]}^2+a_2{\left[\frac{B+T\left(F_n;x,y\right)-r_1}{2}\right]}^2\end{array}$

其中：

$T\left(f\left(C_1,F_n\right);x,y\right)=yT\left(F_{n-1}^{+};x,y\right)$

$T\left(f\left(C_{\text{2}},F_n\right);x,y\right)=AT\left(F_n;x,y\right)+ByT\left(F_{n-1}^{+};x,y\right)$

解得：

$\{\begin{array}{l}{a}_1=\frac{\left[y{r}_{\text{1}}-yT\left(F_n;x,y\right)+By\right]T\left(F_{n-1}^{+};x,y\right)+2AT\left(F_n;x,y\right)}{r_{\text{1}}\left(B+T\left(F_n;x,y\right)+r\right)}\\ a_2=\frac{\left[y{r}_{\text{1}}+yT\left(F_n;x,y\right)-By\right]T\left(F_{n-1}^{+};x,y\right)-2AT\left(F_n;x,y\right)}{r_{\text{1}}\left(B+T\left(F_n;x,y\right)-r\right)}\end{array}$

综上所述，花图 $f\left(C_m,F_n\right)$ 的Tutte多项式可以写为：

$\begin{array}{c}T\left(f\left(C_m,F_n\right);x,y\right)=\frac{\left[y{r}_{\text{1}}-yT\left(F_n;x,y\right)+By\right]T\left(F_{n-1}^{+};x,y\right)+2AT\left(F_n;x,y\right)}{r_{\text{1}}\left(B+T\left(F_n;x,y\right)+r\right)}{\left(\frac{B+T\left(F_n;x,y\right)+r_{\text{1}}}{\text{2}}\right)}^n\\ +\frac{\left[y{r}_{\text{1}}+yT\left(F_n;x,y\right)-By\right]T\left(F_{n-1}^{+};x,y\right)-2AT\left(F_n;x,y\right)}{r_{\text{1}}\left(B+T\left(F_n;x,y\right)-r\right)}{\left(\frac{B+T\left(F_n;x,y\right)-r_{\text{1}}}{\text{2}}\right)}^n\end{array}$

其中：

$\begin{array}{c}A=\frac{\left(1+x^2+y-r+xr-xy\right)\left(x+y+1+r\right)}{\text{2}xr\left(1-x-y-r\right)}\left[1-{\left(\frac{x+y+1+r}{\text{2}}\right)}^{n-1}\right]\\ -\frac{\left(1+x^2+y+r-xr-xy\right)\left(x+y+1+r\right)}{\text{2}xr\left(1-x-y+r\right)}\left[1-{\left(\frac{x+y+1-r}{2}\right)}^{n-1}\right]-y+1\end{array}$ ；

$\begin{array}{c}B=\frac{\left(y+x^2+x-x{y}^2+y^{2}r+yr+xr-y^3\right)}{r\left(1-x-y-r\right)}\left[\text{1}-{\left(\frac{x+y+1+r}{2}\right)}^{n-1}\right]\\ -\frac{\left(y+x^2+x-x{y}^2-y^{2}r-yr-xr-y^3\right)}{r\left(1-x-y+r\right)}\left[\text{1}-{\left(\frac{x+y+1-r}{2}\right)}^{n-1}\right]-y^2+1\end{array}$

$T\left(F_n;x,y\right)=\left(\frac{1+x^2+y-r+xr-xy}{\text{2}xr}\right){\left(\frac{x+y+1+r}{2}\right)}^n-\left(\frac{1+x^2+y+r-xr-xy}{\text{2}xr}\right){\left(\frac{x+y+1-r}{2}\right)}^n$

$\begin{array}{c}T\left(F_n^{+};x,y\right)=\frac{y+x^2+x-x{y}^2+y^{2}r+yr+xr-y^3}{r\left(x+y+1+r\right)}{\left(\frac{x+y+1+r}{2}\right)}^n\\ -\frac{y+x^2+x-x{y}^2-y^{2}r-yr-xr-y^3}{r\left(x+y+1-r\right)}{\left(\frac{x+y+1-r}{2}\right)}^n\end{array}$

$r=\sqrt{{\left(x+y+1\right)}^2-4xy}$ ； $r_{\text{1}}=\sqrt{{\left[B+T\left(F_n;x,y\right)\right]}^2-4BT\left(F_n;x,y\right)}$

证毕。

4. 总结

本文主要研究了一类花图 $f\left(C_m,F_n\right)$ 的Tutte多项式，通过利用Tutte多项式的一些性质计算得到了花图 $f\left(C_m,F_n\right)$ Tutte多项式的具体表达式。由于Tutte多项式包含图的大量信息，未来还可以通过Tutte多项式去研究花图的生成树数目、连通生成子图数目等。