热方程及其类似形式的傅里叶变换解

Thermal Equations and Their Similar Forms of Fourier Transform Solutions

摘要: 本文考虑热方程及其类似形式的傅里叶变换解，从经典的一维及高维热方程的傅里叶变换求解推广到具有热方程类似形式的一维及高维偏微分方程的傅里叶变换解。

Abstract: In this paper, we consider the solutions of the thermal equation and its similar form of Fourier transform, and generalize from the Fourier transform solution of the classical one-dimensional and high-dimensional thermal equations to the Fourier transform solution of one-dimensional and high-dimensional partial differential equations with a similar form of the thermal equation.

1. 背景介绍

具有初值条件的一维及高维热方程及其类似形式的偏微分方程分别有如下表示形式

$\{\begin{array}{l}{u}_t-u_{xx}=0,-\infty <x<\infty ,t>0.\\ u=\phi ,-\infty <x<\infty ,t=0.\end{array}$ (1.1)

$\{\begin{array}{l}{u}_t-\Delta u=0,\left(x,t\right)\in {ℝ}^n\times \left(0,\infty \right).\\ u=g,x\in {ℝ}^n,t=0.\end{array}\left(n\ge 2\right)$ (1.2)

$\{\begin{array}{l}{u}_{tt}+u_{xxxx}=0,-\infty <x<\infty ,t>0,\\ u\left(x,0\right)=\phi \left(x\right),u_t\left(x,0\right)=0.\end{array}$ (1.3)

$\{\begin{array}{l}{u}_{tt}+{\Delta }^{2}u=0,\left(x,t\right)\in {ℝ}^n\times \left(0,\infty \right),\\ u\left(x,0\right)=g,u_t\left(x,0\right)=0.\end{array}\left(n\ge 2\right)$ (1.4)

其一维和高维热方程的基本解在数学、物理、工程中有很多广泛的应用，对于求解偏微分方程和在热学工程领域极其重要，具体可以参考文献 [1] [2] [3] [4] [5] 。具有热方程类似形式的偏微分方程也是在物理问题中推导而来，在微分方程动力系统，偏微分方程中具有重要意义，具体可见文献 [6] [7] [8] [9] 。

不失一般性，将本文中的热系数都设为1，且都是齐次形式偏微分方程，对于非齐次形式求解需要加积分因子而这并不影响基本解的性质，热核都是相应的形式，具体参见文献 [10] 。

本文先分别对方程(1.1)和(1.2)利用傅里叶变换进行求解，得到基本解的形式，后对具有热方程类似形式的偏微分方程利用傅里叶变换进行求解，得到了其对应的基本解，对一维和高维的热方程求解具体参考了文献 [11] ，本文对其重新求解是为了突出其重要性，求解过程对接下来具有热方程类似形式的偏微分方程求解提供了很好的思路，由于文章中大量用到了傅里叶变换，我们需要做一些准备性工作。

2. 准备工作

定义2.1 (反演公式)设 $f\left(x\right)$ 是连续、分段光滑且绝对可积的。如果设

$F\left(\lambda \right)=\frac{1}{\sqrt{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }f\left(x\right){\text{e}}^{-\text{i}\lambda x}\text{d}x}$

那么对所有的x，有

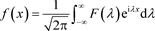
函数 $F\left(\lambda \right)$ 称为 $f\left(x\right)$ 的傅里叶变换，通常记为 ${\left(f\left(x\right)\right)}^{\wedge }$ 或 $\hat{f}\left(\lambda \right)$ 。而 $f\left(x\right)$ 称为 $F\left(\lambda \right)$ 的傅里叶逆变换，通常记为 ${\left(F\left(\lambda \right)\right)}^{\vee }$ 。

引理2.2 若 $f_i\left(x\right)\in L^1\left(-\infty ,\infty \right)$ ， $a_i\left(i=1,2\right)$ 为任意常数，则

${\left(a_1{f}_1+\cdots +a_n{f}_n\right)}^{\wedge }=a_1\widehat{f_1}+\cdots +a_1\widehat{f_n}$

引理2.3 若 $f\left(x\right)$ ， $f^{\prime }\left(x\right)\in C\left(-\infty ,\infty \right)\cap L^1\left(-\infty ,\infty \right)$ ，则

${\left(\frac{\text{d}f}{\text{d}x}\right)}^{\wedge }=\text{i}\lambda \hat{f}(\; \lambda \; )$

证明：见文献 [12] 。

推论2.4 若 $f\left(x\right),f^{\prime }\left(x\right),\cdots ,f^{\left(m\right)}\left(x\right)\in C\left(-\infty ,\infty \right)\cap L^1\left(-\infty ,\infty \right)$ ，则

${\left(\frac{{\text{d}}^{m}f}{\text{d}{x}^m}\right)}^{\wedge }={\left(\text{i}\lambda \right)}^m\hat{f}\left(m\ge 1\right)$

计算中发现傅里叶变换的对称性质如下：

${\left(f\left(x\right)\right)}^{\wedge }={\left(f\left(-x\right)\right)}^{\vee }$

引入卷积概念如下：

定义2.5 若 $f\left(x\right),g\left(x\right)\in L^1\left(-\infty ,\infty \right)$ ，则f与g的卷积定义为

$\left(f\ast g\right)\left(x\right)={\displaystyle {\int }_{-\infty }^{\infty }f\left(x-t\right)g\left(t\right)\text{d}t}\in L^1\left(-\infty ,\infty \right)$

且有

${\left(f\ast g\right)}^{\wedge }=\sqrt{2\pi }\hat{f}\hat{g}$

引理2.6 若满足定义2.2的假设条件，有

${\left(\hat{f}\ast \hat{g}\right)}^{\vee }=\sqrt{2\pi }fg$

引理2.7 若 $f\left(x\right),g\left(x\right)\in L^1\left(-\infty ,\infty \right)$ ，则

${\left(\hat{f}\hat{g}\right)}^{\vee }=\frac{1}{\sqrt{2\pi }}f\ast g$

3. 求解过程

视t为参数，对方程(1.1)两边及初始条件关于x进行傅里叶变换，利用引理2.2和引理2.3我们有

$\{\begin{array}{l}{\hat{u}}_t+{\lambda }^2\hat{u}=0,\hfill \\ {\hat{u}|}_{t=0}=\hat{\phi }\left(\lambda \right),\hfill \end{array}$ (3.1)

解这样一个关于t的常微分方程，得到

$\hat{u}\left(\lambda ,t\right)=\hat{\phi }{\text{e}}^{-{\lambda }^{2}t}$

对上式两边进行反演，由引理2.7得

$u\left(x,t\right)={\left(\hat{\phi }{\text{e}}^{-{\lambda }^{2}t}\right)}^{\vee }$

关键是求出 ${\text{e}}^{-{\lambda }^{2}t}$ 是某个函数如 $g\left(x,t\right)$ 关于x的傅里叶变换，计算发现

$g\left(x,t\right)=\frac{1}{\sqrt{2t}}{\text{e}}^{-\frac{x^2}{4t}}$

由引理2.6和引理2.7，我们有

${\left(\hat{\phi }{\text{e}}^{-{\lambda }^{2}t}\right)}^{\vee }={\left(\hat{\phi }\hat{g}\right)}^{\vee }=\frac{1}{\sqrt{2\pi }}\phi \ast g=\frac{1}{2\sqrt{\pi t}}{\displaystyle {\int }_{-\infty }^{\infty }\phi \left(\xi \right){\text{e}}^{-\frac{{\left(x-\xi \right)}^2}{4t}}\text{d}\xi }$

即

$u\left(x,t\right)={\displaystyle {\int }_{-\infty }^{\infty }K\left(x-\xi ,t\right)\phi \left(\xi \right)\text{d}\xi }$ (3.2)

为齐次一维热方程基本解。其中

$K\left(x,t\right)=\{\begin{array}{l}\frac{1}{2\sqrt{\pi t}}{\text{e}}^{-\frac{x^2}{4t}},t>0,\\ 0,t\le 0.\end{array}$ (3.3)

称为齐次一维热方程的热核。

接下来，对方程(1.2)进行求解，与求解方程(1.1)类似，需要注意的是此时 $x,\xi$ 和 $\lambda$ 为 $n\left(n\ge 2\right)$ 维向量，对方程(1.2)两边和初始条件进行傅里叶变换，我们有

$\{\begin{array}{l}{\hat{u}}_t+{\left|\lambda \right|}^2\hat{u}=0,\hfill \\ {\hat{u}|}_{t=0}=\hat{g},\hfill \end{array}$ (3.4)

求解这样一个常微分方程并进行反演得到

$u\left(x,t\right)=\frac{1}{{\left(4\pi t\right)}^{n/2}}{\displaystyle {\int }_{{ℝ}^n}{\text{e}}^{-\frac{{\left|x-\xi \right|}^2}{4t}g\left(\xi \right)\text{d}\xi }},$ (3.5)

为齐次n维热方程的基本解，热核也有相对应的形式。

对于具有热方程类似形式的方程(1.3)求解需要具体问题具体看待，我们采用傅里叶变换求解，先对方程两边及初始条件关于x进行傅里叶变换，得到

$\{\begin{array}{l}{\hat{u}}_{tt}+{\lambda }^4\hat{u}=0,\\ \hat{u}\left(\lambda ,0\right)=\hat{\phi }\left(\lambda \right),\\ {\hat{u}}_t\left(\lambda ,0\right)=0,\end{array}$ (3.6)

解这样带参数 $\lambda$ 的常微分方程初值问题，得

$\hat{u}\left(\lambda ,t\right)=\hat{\phi }\left(\lambda \right)\cos {\lambda }^{2}t,$

对上式两端进行反演，有

$\begin{array}{c}u\left(x,t\right)={\left(\hat{\phi }\left(\lambda \right)\cos {\lambda }^{2}t\right)}^{\vee }\\ =\frac{1}{\sqrt{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }\hat{\phi }\left(\lambda \right)\cos {\lambda }^{2}t{\text{e}}^{\text{i}\lambda x}\text{d}\lambda }\\ =\frac{1}{2\sqrt{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }\hat{\phi }\left(\lambda \right)\left({\text{e}}^{\text{i}{\lambda }^{2}t}+{\text{e}}^{-\text{i}{\lambda }^{2}t}\right){\text{e}}^{\text{i}\lambda x}\text{d}\lambda }\\ :={\displaystyle \underset{k=1}{\overset{2}{\sum }}{I}_k}\end{array}$

计算 $I_1$ ，有

$\frac{1}{\sqrt{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{\text{i}{\lambda }^{2}t}{\text{e}}^{\text{i}\lambda x}\text{d}\lambda }=\frac{1}{\sqrt{2\pi }}{\text{e}}^{-\text{i}\frac{x^2}{4t}}{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{\text{i}t{\left(\lambda +\frac{x}{2t}\right)}^2}\text{d}\lambda }$

将上式变换，令 $\xi =\sqrt{t}\left(\lambda +\frac{x}{2t}\right)$ ，并利用欧拉公式，可将上式化为

$\begin{array}{c}\frac{1}{\sqrt{2\pi }}{\text{e}}^{-\text{i}\frac{x^2}{4at}}\frac{1}{\sqrt{t}}{\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{\text{i}{\xi }^2}\text{d}\xi }=\frac{1}{\sqrt{2\pi }}{\text{e}}^{-\text{i}\frac{x^2}{4t}}\frac{1}{\sqrt{t}}\cdot {\text{e}}^{\text{i}\frac{\pi }{4}}\sqrt{\pi }\\ =\frac{1}{\sqrt{2t}}{\text{e}}^{\text{i}\left(\frac{\pi }{4}-\frac{x^2}{4t}\right)}\\ =\frac{1}{\sqrt{2t}}\left[\cos \left(\frac{\pi }{4}-\frac{x^2}{4t}\right)+i\sin \left(\frac{\pi }{4}-\frac{x^2}{4t}\right)\right].\end{array}$

根据欧拉公式，我们发现

${\left({\text{e}}^{\text{i}{\lambda }^{2}t}\right)}^{\vee }={\left(\cos {\lambda }^{2}t+\text{i}\sin {\lambda }^{2}t\right)}^{\vee }$

在此实函数 $\cos {\lambda }^{2}t$ 和 $\sin {\lambda }^{2}t$ 的傅里叶逆变换还是实函数，由此我们可得

${\left(\cos {\lambda }^{2}t\right)}^{\vee }=\frac{1}{\sqrt{2t}}\cos \left(\frac{\pi }{4}-\frac{x^2}{4t}\right)$

${(\sin {\lambda }^{2}t)}^{\vee }=\frac{1}{\sqrt{2t}}\sin \left(\frac{\pi }{4}-\frac{x^2}{4t}\right)$

根据引理2.7，我们有

${\left(\hat{\phi }\left(\lambda \right)\cos {\lambda }^{2}t\right)}^{\vee }=\frac{1}{\sqrt{2\pi }}\left[\phi \left(x\right)\ast {\left(\cos {\lambda }^{2}t\right)}^{\vee }\right]$

所以我们得到

$\begin{array}{c}\frac{1}{\sqrt{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }\hat{\phi }\left(\lambda \right)\cos {\lambda }^{2}t{\text{e}}^{\text{i}\lambda x}\text{d}\lambda }=\frac{1}{\sqrt{2\pi }}\phi \left(x\right)\ast \frac{1}{\sqrt{2t}}\cos \left(\frac{\pi }{4}-\frac{x^2}{4t}\right)\\ =\frac{1}{2\sqrt{t\pi }}{\displaystyle {\int }_{-\infty }^{\infty }\phi \left(\xi \right)\cos \left(\frac{\pi }{4}-\frac{{\left(x-\xi \right)}^2}{4t}\right)\text{d}\xi }\end{array}$

故方程(1.3)的基本解如下

$u\left(x,t\right)=\frac{1}{2\sqrt{\pi t}}{\displaystyle {\int }_{-\infty }^{\infty }\phi }\left(\xi \right)\cos \left(\frac{\pi }{4}-\frac{{\left(x-\xi \right)}^2}{4t}\right)\text{d}\xi .$ (3.7)

方程(1.3)的热核为

$K\left(x,t\right)=\{\begin{array}{l}\mathrm{Re}\left(\frac{1}{2\sqrt{\pi t}}{\text{e}}^{-i\left(\frac{x^2}{4t}-\frac{\pi }{4}\right)}\right),t>0,\\ 0,t\le 0.\end{array}$

最后，对方程(1.4)进行求解，与求解方程(1.3)类似，同样需要注意的是此时 $x,\xi$ 和 $\lambda$ 为 $n\left(n\ge 2\right)$ 维向量，对方程(1.4)两边和初始条件进行傅里叶变换，我们有

$\{\begin{array}{l}{\hat{u}}_{tt}+{\left|\lambda \right|}^4\hat{u}=0,\\ \hat{u}\left(\lambda ,0\right)=\hat{g},\\ {\hat{u}}_t\left(\lambda ,0\right)=0,\end{array}$ (3.8)

解这样的二阶常微分方程，得到 $\hat{u}\left(\lambda ,t\right)=\hat{\phi }\left(\lambda \right)\cos {\left|\lambda \right|}^{2}t$ 。

对上式两端进行反演，得到

$u\left(x,t\right)=\frac{1}{{\left(2\pi \right)}^n}\frac{1}{\sqrt{\pi t}}{\displaystyle {\int }_{-\infty }^{\infty }\phi \left(\xi \right)\cos \left(\frac{\pi }{4}-\frac{{\left(x-\xi \right)}^2}{4t}\right)\text{d}\xi }$ (3.9)

也有相对应的热核形式。

更一般的具有热方程类似形式的偏微分方程如下

$\{\begin{array}{l}\frac{{\partial }^{n}u}{\partial t^n}+{\Delta }^{n}u=0,\left(x,t\right)\in {ℝ}^n\times \left(0,\infty \right),\\ u\left(x,0\right)=g,{\frac{\partial u}{\partial t}|}_{t=0}={\frac{{\partial }^{2}u}{\partial t^2}|}_{t=0}=\cdots ={\frac{{\partial }^{n-1}u}{\partial t^n}|}_{t=0}=0.\end{array}\left(n>2\right)$ (3.10)

利用傅里叶变换化为带有初值问题的n阶常微分方程，对于其n次特征方程有根式解，利用推论2.4也可以得到方程(3.10)的基本解和热核。形式较为复杂，这里不再赘述，但值得指出的是在现代偏微分方程理论框架下，傅里叶变换依然大有可为，详见文献 [13] [14] 。