带遗产计划和非流动性资产的DC型养老金的最优投资组合问题

Optimal Portfolio Problem for a DC Pension Plan with Estate Planning and Illiquid Assets

摘要: 本文探讨了当缴费确定(DC)型养老金计划考虑非流动性资产投资时的最优投资组合问题，并研究非流动性对投资组合选择的影响，同时还涉及养老金计划参与者的遗产计划、退休前随机劳动工资、退休后的生活保障和通货膨胀的风险。建模时，假设投资者可投资于无风险资产、股票和指数债券外，还有一种非流动性资产，我们考虑一个定期投资，即只能在时间0时进行交易，并在退休时提供回报。投资者同时表现出寻求风险和厌恶损失的行为，退休时投资回报的效用为S型。我们首先应用Legendre-Fenchel变换得到最优终端财富，然后采用鞅方法得到完整市场中最优投资策略和财富过程，并给出非流动性资产的最优交易策略，解决了投资者的最优投资组合问题。在此基础上，结合一些数字结论来分析模型参数和一些特征对投资策略的影响。

Abstract: This paper explores the optimal portfolio problem when a defined contribution (DC) pension plan considers investments in illiquid assets and examines the impact of illiquidity on portfolio choice, as well as the risks of estate planning, stochastic pre-retirement labor wages, post-retirement living security, and inflation for pension plan participants. For modeling, it is assumed that an investor can invest in an illiquid asset in addition to risk-free assets, stocks and indexed bonds, and we con-sider a periodic investment that can only be traded at time 0 and provides returns at retirement. The investor exhibits both risk-seeking and loss averse behavior, and the S-shaped utility from the investment return at retirement. We first apply the Legendre-Fenchel transformation to obtain the optimal terminal wealth, and then use the harnessing method to obtain the optimal investment strategy and wealth process in the complete market, and give the optimal trading strategy for illiq-uid assets, which solves the optimal portfolio problem for investors. On this basis, some numerical conclusions are combined to analyze the effects of model parameters and some features on invest-ment strategies.

1. 引言

养老基金计划是一种为了保障老年人生活权益的制度，通过向个人或企业征收养老金税或者由企业和个人共同缴纳的方式，它关系着居民在退休后的生活水平和质量，是当前社会保障体系制度中重要的组成部分。随着中国老年人口的总数不断提高，收支规模不断扩大，养老金基金管理者面临着如何缓解社会保障体系承受的支付压力这一难题，那么提高资金运用的收益率，关注养老金的升值保值，进行多元化的投资，并且兼顾养老金风险管理，是管理者需要共同研究的问题。

根据缴费和给付方式的不同，养老金主要分为两类：收益确定(DB)型养老计划和缴费确定(DC)型养老计划。在DC型模式下，企业年金计划的缴费比例或金额是确定的，投资风险由计划参与者自己承担，DC型养老金的运作比DB型更加透明，更方便有关部门实施监管。对于DC型养老金投资策略的研究方法主要有动态规划原理、极大值原理以及凸对偶鞅方法等。动态规划原理是将最优控制问题与一个偏微分方程(即HJB方程)之间建立联系。极大值原理则是求解一个倒向随机微分方程，并使得广义哈密顿算子满足极大值条件。对于凸对偶鞅方法是由Cox和Huang [1] 在完备市场下，结合凸分析和随机分析，应用lagrange乘数理论和等价鞅测度及鞅表示定理，通过等价的静态规划根据既定目标来解决相应的问题。蔡晶晶和董迎辉等 [2] 应用最优化凹问题和鞅方法，在风险厌恶的基金管理者在最低保障和VaR约束下，研究了关于DC型养老金的最优投资策略问题。Bian和Li [3] 研究了DC型养老金成员退休前后的两个多周期均值方差投资问题，给出了具有随机利率和随机收入的时间一致策略。Wang和Li [4] 利用滤波技术和动态规划原理，研究并得到了在不完全信息和模糊厌恶下DC型养老金的最优投资策略。王佩等 [5] 在均值–方差准则下，利用随机最优控制方法研究和博弈论框架下研究了可投资衍生品的DC型养老金计划的均衡投资策略。史爱林和李仲飞 [6] 研究了在考虑遗产动机和最低业绩约束下的DC型养老金的优化投资问题。Chen等 [7] 研究了在通货膨胀和兼顾成员退休后的最低生活保障的基础上，损失厌恶型管理者的DC型养老金的资产配置问题。以上文献的工作都是研究养老基金仅投资于金融市场中的流动性资产时的最优投资问题，由于非流动性资产的持有体量占比不可忽略，因此在金融投资组合中考虑非流动性资产的交易是合理并有趣的。

非流动资产是指流动性资产以外的资产，主要包括持有到期投资、长期应收款、长期股权投资、投资性房地产、固定资产、长期待摊费用等，相较于流动性资产。由于养老基金投资周期时间长，Dirk W. G. A. Broeders等 [8] 认为非流动性资产是养老金投资的有效途径，其探究了DB型养老基金在流动性和资金需求下的非流动性资产配置问题，结果表明投资于非流动性资产类别。Bordag等 [9] 的工作研究了具有非流动性资产组合的最优分配–消费问题。Desmettre和Seifried等人 [10] 提出一个新的框架来研究含有定期证券的最优资产配置问题，这种非流动性的定期证券只在时间零点进行交易。基于这个框架，Chen和Li等 [11] 研究了损失厌恶型养老金投资者考虑非流动性资产时的投资组合选择。

基于上述关于养老金计划的最优投资组合问题的相关文献研究，本文探究当损失厌恶的基金管理者带有对遗产计划需求，并且同时含有非流动性资产的交易时的DC型养老金的最优投资组合问题。这里我们的工作不光研究养老金计划在累计阶段的资产配置情况，同时还兼顾退休后的分配阶段。本文采用Legendre-Fenchel变换和鞅方法得到以下结果：(1) 在兼顾遗产计划和确定非流动性资产交易策略的基础上，讨论了不同市场环境和基准线下的三种情形的最优终端盈余和最优终端总财富；(2) 给出了任意时刻的最优投资策略和财富过程，并进行数值分析，探讨非流动性对投资组合选择的影响及一些特征对投资策略的影响。

2. 模型建立

在本节中，本文为DC型养老金投资者建立了一个带有非流动性资产的资产组合配置模型，同时考虑到投资周期长所带来的通货膨胀风险。在这个模型中，研究了一个有限的时间跨度 $\left[0,T\right]$ ，其中T是退休时刻。此外，还有一个投资非流动性资产的机会，这种定期投资与其他三种流动性资产股票、债券、无风险资产相比，它只能在投资期开始时进行交易，并在退休时提供一次性的回报。同时投资者表现出寻求风险和厌恶损失的行为，并且有随机的劳动工资流。

2.1. 投资选择

设 $\left\{\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathcal{P}\right\}$ 是完备的概率空间，其中 $\mathcal{F}=\sigma \left({\displaystyle {\cup }_{t\ge 0}{\mathcal{F}}_t}\right)$ 是 $\sigma$ 代数， ${\mathcal{F}}_t=\left\{W\left(s\right);0\le s\le t\right\}$ 是到t时刻为止所掌握的所有市场信息， $\mathbb{W}\left(t\right):={\left(W_1\left(t\right),W_2\left(t\right)\right)}^{\prime }$ 为二维布朗运动， $W_1\left(t\right)$ 和 $W_2\left(t\right)$ 相互独立。

由于养老金计划累积阶段的周期长的特点，通货膨胀会对养老基金的实际回报率有着很大的影响，因此本节引入指数债券来对冲通货膨胀风险。在这个带有非流动性资产的模型中，考虑通货膨胀所带来的风险是具有意义的，我们假设金融市场由无风险资产，指数债券和股票这三种可交易的流动性资产组成。

无风险资产的价格满足常微分方程

$\frac{\text{d}B\left(t\right)}{B\left(t\right)}=R\text{d}t,B\left(0\right)=b_0,$ (1)

其中 $R>0$ 是名义收益率。

定义随机价格指数，满足随机微分方程

$\frac{\text{d}P\left(t\right)}{P\left(t\right)}={\mu }_I\text{d}t+{\sigma }_I\text{d}{W}_1\left(t\right),P\left(0\right)=p_0>0,$ (2)

其中 ${\mu }_I>0$ 是价格指数预期增长率， ${\sigma }_I>0$ 是波动率。

指数债券价格满足下式

$\frac{\text{d}I\left(t\right)}{I\left(t\right)}=r\text{d}t+\frac{\text{d}P\left(t\right)}{P\left(t\right)}=\left(r+{\mu }_I\right)\text{d}t+{\sigma }_I\text{d}{W}_1\left(t\right),$ (3)

其中 $I\left(0\right)=i_0$ ，r是指数债券的实际回报率。

股票的价格由下式给出

$\begin{array}{c}\frac{\text{d}S\left(t\right)}{S\left(t\right)}={\mu }_S\text{d}t+{\sigma }_S\left({\rho }_{IS}\text{d}{W}_1\left(t\right)+\sqrt{1-{\rho }_{IS}^2}\text{d}{W}_2\left(t\right)\right)\\ ={\mu }_S\text{d}t+{\hat{\sigma }}_S^T\text{d}\mathbb{W}\left(t\right),S\left(0\right)=s_0>0,\end{array}$ (4)

其中 ${\mu }_S>0$ 表示股票的预期收益率， ${\sigma }_S>0$ 是波动率， ${\hat{\sigma }}_S={\left({\sigma }_S{\rho }_{IS},{\sigma }_S\sqrt{1-{\rho }_{IS}^2}\right)}^{\prime }$ 。 ${\rho }_{IS}$ 表示股票和指数债券价格的相关系数， ${\rho }_{IS}\in \left[-1,1\right]$ 是一个常数。

定义波动率矩阵，它是非奇异的

$\Sigma =\left(\begin{array}{cc}{\sigma }_I& 0\\ {\sigma }_S{\rho }_{IS}& {\sigma }_S\sqrt{1-{\rho }_{IS}^2}\end{array}\right),$ (5)

定义市场风险价格(指数债券和股票价格的夏普比率向量)

$\Xi ={\Sigma }^{-1}\left(\begin{array}{c}r+{\mu }_I-R\\ {\mu }_S-R\end{array}\right)=\left(\begin{array}{c}{\xi }_1\\ {\xi }_2\end{array}\right)=\left(\begin{array}{c}\frac{r+{\mu }_I-R}{{\sigma }_I}\\ \frac{1}{\sqrt{1-{\rho }_{IS}^2}}\left(\frac{{\mu }_S-R}{{\sigma }_S}-\frac{{\rho }_{IS}\left(r+{\mu }_I-R\right)}{{\sigma }_I}\right)\end{array}\right).$ (6)

定义价格核过程(随机贴现因子) $K(\; t\; )$

$K\left(t\right)={\text{e}}^{-\left(R+\frac{1}{2}{\Vert \Xi \Vert }^2\right)t-{\Xi }^{\prime }\mathbb{W}\left(t\right)},$ (7)

通过计算可得

$\frac{\text{d}K\left(t\right)}{K\left(t\right)}=-R\text{d}t-{\Xi }^{\prime }\text{d}\mathbb{W}\left(t\right),K\left(0\right)=1.$ (8)

除了上述三种流动性交易资产外，我们考虑一种定期投资，投资者还可以投资于一种非流动性资产 $F\left(t\right)$ 。在初始时间0，非流动性资产的价格为 $F\left(0\right)$ ，随着时间的变化，其价格满足以下动态方程

$\begin{array}{c}\frac{\text{d}F\left(t\right)}{F\left(t\right)}={\mu }_F\text{d}t+{\sigma }_F\left({\rho }_{IF}\text{d}{W}_1\left(t\right)+{\rho }_{SF}\text{d}{W}_2\left(t\right)+\sqrt{1-{\rho }_{IF}^2-{\rho }_{SF}^2}\text{d}{W}_F\left(t\right)\right)\\ ={\mu }_F\text{d}t+{{\hat{\sigma }}^{\prime }}_F\text{d}\mathbb{W}\left(t\right)+\sqrt{1-{\rho }_{IF}^2-{\rho }_{SF}^2}\text{d}{W}_F\left(t\right),\end{array}$ (9)

这里 ${\mu }_F$ 表示收益率。 $W_F\left(t\right)$ 是独立于 $W_1\left(t\right)$ 和 $W_2\left(t\right)$ 的标准布朗运动。 ${\rho }_{IF}$ 和 ${\rho }_{SF}$ 分别表示非流动性资产与指数债券及股票之间的相关性。其中 ${\hat{\sigma }}_F={\left({\sigma }_F{\rho }_{IF},{\sigma }_F{\rho }_{SF}\right)}^{\prime }$ 。投资者在初始时间0购买价格为 $F\left(0\right)$ 的非流动性资产，那么他在退休时获得 $F\left(T\right)$ 的随机回报。

由于考虑到通货膨胀的风险和成员有随机的收入，则随机工资流满足以下动态方程

$\begin{array}{c}\frac{\text{d}Y\left(t\right)}{Y\left(t\right)}={\mu }_Y\text{d}t+{\sigma }_Y\left({\rho }_{IY}\text{d}{W}_1\left(t\right)+\sqrt{1-{\rho }_{IY}^2}\text{d}{W}_2\left(t\right)\right)\\ ={\mu }_Y\text{d}t+{{\hat{\sigma }}^{\prime }}_Y\text{d}\mathbb{W}\left(t\right),\end{array}$ (10)

其中 ${\mu }_Y>0$ 为工资的预期增长率， ${\sigma }_Y>0$ 是工资波动率， ${\hat{\sigma }}_Y={\left({\sigma }_Y{\rho }_{IY},{\sigma }_Y\sqrt{1-{\rho }_{IY}^2}\right)}^{\prime }$ 。 ${\rho }_{IY}$ 表示指数债券和工资收入的相关系数。这里假设 ${\rho }_{IY}>0$ ，反映了当通货膨胀变大时，市场环境变恶劣，成员希望有更高的劳动收入。

2.2. 财富过程和投资者偏好

设投资者在初始时刻0的初始总财富为 $x_0$ ，她花费 $\psi F\left(0\right)$ 的资产买入了 $\psi$ 的非流动性资产，在此之后参与流动性市场的交易。设 $\pi \left(t\right)={\left({\pi }_1\left(t\right),{\pi }_2\left(t\right)\right)}^{\prime }$ ，其中 ${\pi }_1\left(t\right)$ 、 ${\pi }_2\left(t\right)$ 分别表示投资于指数债券和股票的流动性资金比例。c是缴费率。故投资于流动性市场的流动性财富过程 $X^{\pi ,\psi }\left(t\right)$ 的动态方程为

$\begin{array}{l}\text{d}{X}^{\pi ,\psi }\left(t\right)=R{X}^{\pi ,\psi }\left(t\right)\text{d}t+X^{\pi ,\psi }\left(t\right){\pi }^{\prime }\left(t\right)\Sigma \left(\Xi \text{d}t+\text{d}\mathbb{W}\left(t\right)\right)+cY\left(t\right)\text{d}t,\\ X^{\pi ,\psi }\left(0\right)=x_0-\psi F\left(0\right),\end{array}$ (11)

$t\in \left[0,T\right]$ 。特别地，在退休时，非流动性资产给予 $\psi F\left(T\right)$ 的回报，因此带有非流动性资产交易的最终总财富为 $X_T=X^{\pi ,\psi }\left(T\right)+\psi F\left(T\right)$ 。

同时我们不能忽略人力资本对养老金计划有着很大的贡献。根据Chen等 [7] 的设定，T为退休时刻， $\bar{T}$ 是死亡时刻(为确定的常数)，则养老金计划成员未来预期贡献在时刻t的累积贴现值为

$M\left(t\right)=c{\mathbb{E}}_t\left[{\displaystyle {\int }_t^T\frac{K\left(s\right)}{K\left(t\right)}Y\left(s\right)\text{d}s}\right],$ (12)

其中 ${\mathbb{E}}_t[\cdot ]=\mathbb{E}\left[\cdot |{\mathcal{F}}_t\right]$ 表示在给定时刻t的信息 ${\mathcal{F}}_t$ 下的条件期望。通过计算可得到

$M\left(t\right)=\frac{1}{{\tau }_1}\left({\text{e}}^{{\tau }_1\left(T-t\right)}-1\right)cY\left(t\right),$ (13)

其中 ${\tau }_1={\mu }_Y-R-{\Xi }^{\prime }{\hat{\sigma }}_Y$ ， $M\left(t\right)$ 求微分可得

$\text{d}M\left(t\right)=RM\left(t\right)\text{d}t+M\left(t\right){{\hat{\sigma }}^{\prime }}_Y\left(\text{Ξd}t+\text{d}\mathbb{W}\left(t\right)\right)-cY\left(t\right)\text{d}t.$ (14)

为了后续计算简化，记 $m_0\equiv M\left(0\right)$ 。

同时定义养老金计划成员在退休后的最低生活水平为 $l\left(t\right)$ ，满足方程

$\frac{\text{d}l\left(t\right)}{l\left(t\right)}={\mu }_l\text{d}t+{{\hat{\sigma }}^{\prime }}_l\text{d}\mathbb{W}\left(t\right),$ (15)

其中 ${\mu }_l\ge 0$ 是平均增长率， ${\sigma }_l\ge 0$ 是波动率， ${\hat{\sigma }}_l={\left({\sigma }_l{\rho }_{Il},{\sigma }_l\sqrt{1-{\rho }_{Il}^2}\right)}^{\prime }$ 。由此可定义时刻t的最低生活保障

$L\left(t\right)={\mathbb{E}}_t\left[{\displaystyle {\int }_t^{\bar{T}}\frac{K\left(s\right)}{K\left(t\right)}l\left(s\right)\text{d}s}\right],$ (16)

通过计算可得

$L\left(t\right)=\frac{1}{{\tau }_2}\left({\text{e}}^{{\tau }_2\left(\bar{T}-t\right)}-{\text{e}}^{{\tau }_2\left(T-t\right)}\right)l\left(t\right),$ (17)

其中 ${\tau }_2={\mu }_l-R-{\Xi }^{\prime }{\hat{\sigma }}_l$ ，对 $L\left(t\right)$ 求微分可得

$\text{d}L\left(t\right)=RL\left(t\right)\text{d}t+L\left(t\right){{\hat{\sigma }}^{\prime }}_l\left(\Xi \text{d}t+\text{d}\mathbb{W}\left(t\right)\right).$ (18)

记 $L_0\equiv L\left(0\right)$ 。

在研究流动性资产和非流动性资产的最优投资问题中，几乎大部分工作都采用CRRA型或CARA型效用函数来描述投资者的投资偏好，但大多数投资者是损失厌恶者，他们更加关注财富的变化而非最终状态，因此本文选择使用Kahneman和Tversky (1979) [12] 提出的一个框架，即前景理论。因此S型偏好的投资者表现出损失厌恶和寻求风险的行为，其效用函数为

$U\left(X\left(T\right)\right)=\{\begin{array}{l}-A{\left(\theta -X\left(T\right)\right)}^{{\gamma }_1},X\left(T\right)\le \theta ,\\ {\left(\theta -X\left(T\right)\right)}^{{\gamma }_2},X\left(T\right)>\theta ,\end{array}$ (19)

其中，A为正常数， $A>1$ 表明损失厌恶成立； ${\gamma }_1$ 和 ${\gamma }_2$ 是损失和收益的曲率参数， ${\gamma }_1$ 、 ${\gamma }_2$ 分别代表损失厌恶程度和风险厌恶程度， $0<{\gamma }_1<1$ 和 $0<{\gamma }_2<1$ 时对凸凹性成立，在面对收益时是凹函数，表现为风险厌恶，在面对损失时是凸函数，表现出风险偏好的特性； $\theta$ 是预先给定的参考点，参考点 $\theta$ 有着至关重要的作用。

3. 最优投资策略

在这一部分，由于非流动性资产是风险性投资，同时具有市场化和非市场化风险的特点，为了后续的进一步分析，我们用流动性资产的市场来覆盖非流动性资产投资，通过鞅方法来解决优化问题中的闭式解。因此我们假设非流动性资产的价格满足以下动态

$\begin{array}{c}\frac{\text{d}F\left(t\right)}{F\left(t\right)}={\mu }_F\text{d}t+{\sigma }_F\left({\rho }_{IF}\text{d}{W}_1\left(t\right)+{\rho }_{SF}\text{d}{W}_2\left(t\right)\right)\\ ={\mu }_F\text{d}t+{{\hat{\sigma }}^{\prime }}_F\text{d}\mathbb{W}\left(t\right),\end{array}$ (20)

这里 ${\rho }_{SF}=\sqrt{1-{\rho }_{IF}^2}$ ， ${\hat{\sigma }}_F={\left({\sigma }_F{\rho }_{IF},{\sigma }_F\sqrt{1-{\rho }_{IF}^2}\right)}^{\prime }$ 。

定义在t时刻养老金账户的流动性盈余过程

$Z^{\pi ,\psi }\left(t\right)=X^{\pi ,\psi }\left(t\right)+M\left(t\right)-L\left(t\right).$ (21)

上式可以看出，当 $t=T$ 时，明显地 $M\left(T\right)=0$ ，流动性终端盈余 $Z^{\pi ,\psi }\left(T\right)=X^{\pi ,\psi }\left(T\right)-L\left(T\right)$ 。

性质3.1 流动性性盈余过程 ${\left\{Z^{\pi ,\psi }\left(t\right)\right\}}_{t\in \left[0,T\right]}$ 满足

(i) ${\left\{Z^{\pi ,\psi }\left(t\right)\right\}}_{t\in \left[0,T\right]}$ 是自融资的，且

$\text{d}{Z}^{\pi ,\psi }\left(t\right)=R{Z}^{\pi ,\psi }\left(t\right)\text{d}t+\left(X^{\pi ,\psi }\left(t\right){\pi }^{\prime }\left(t\right)\text{Σ}+M\left(t\right){{\hat{\sigma }}^{\prime }}_Y-L\left(t\right){{\hat{\sigma }}^{\prime }}_l\right)\left(\Xi \text{d}t+\text{d}\mathbb{W}\left(t\right)\right);$ (22)

(ii) $K\left(t\right)Z^{\pi ,\psi }\left(t\right)$ 是鞅；

性质3.1的证明思路类似于Chen等 [7] 。

3.1. 最优化问题

投资者的优化问题是在可容许策略 $\mathcal{A}$ 中选择投资组合 $\left\{\pi ,\psi \right\}$ 使得总终端盈余的期望效用最大化，同时还要兼顾成员的遗产计划：

$\begin{array}{l}\underset{\left(\pi ,\psi \right)\in \mathcal{A}}{\max }\mathbb{E}\left[U\left(Z^{\pi ,\psi }\left(T\right)+\psi F\left(T\right)\right)\right]\\ \text{s}\text{.t}\text{.}{Z}^{\pi ,\psi }\left(T\right)\ge \alpha .\end{array}$ (23)

其中常数 $\alpha$ 表示养老金计划成员具有遗产计划，可以理解为成员死亡时刻的遗产计划在退休时刻的贴现值。我们假设 $\alpha \ge 0$ ，当 $\alpha =0$ 时，养老金计划成员的没有遗产计划，当 $\alpha >0$ 时，成员对遗产计划有需求。

定义3.1 (可容许策略)设投资策略 $\left\{\left(\pi \left(t\right),\psi \right):t\in \left[0,T\right]\right\}$ 是可容许策略， $\psi \ge 0$ ， $\alpha \ge 0$ ，那么下面的四个条件同时成立。

(i) 对于任意的 $t\in \left[0,T\right]$ ， $\pi \left(t\right)$ 是关于 ${\mathcal{F}}_t$ 适应的；

(ii) $\mathbb{E}\left[K\left(T\right)Z^{\pi ,\psi }\left(T\right)\right]<+\infty$ ；

(iii) 上述给定的流动性盈余过程 $Z^{\pi ,\psi }\left(t\right)$ 满足问题(21)中的两个约束；

(iv) $Z^{\pi ,\psi }\left(0\right)\ge z_0^{\min }$ ，其中 $z_0^{\min }=\mathbb{E}\left[\alpha K\left(T\right)\right]$ 。

记所有投资组合的可容许策略的集合为 $\mathcal{A}$ 。

注3.1 从上述满足条件的可允许策略中我们可以得到 $\psi$ 的一个约束条件，当 $t=0$ 时，根据定义 $\alpha \ge 0$ ，有

$X^{\pi ,\psi }\left(0\right)+M\left(0\right)-L\left(0\right)=x_0-\psi F\left(0\right)+m_0-L_0\ge \alpha ,$ (24)

不难看出有 $\psi \le \frac{x_0+m_0-L_0-\alpha }{F\left(0\right)}\le \frac{x_0+m_0-L_0}{F\left(0\right)}\equiv {\psi }_{\max }$ 成立。

3.2. 模型求解

对于 $0\le \psi \le \frac{x_0+m_0-L_0}{F\left(0\right)}\equiv {\psi }_{\max }$ 的约束下，我们要将优化问题(23)转化成等价的静态问题，为了解决这个问题，分两部分进行(参考Desmettre和Seifried [10] )：

第一步：固定非流动性资产的投资 $\psi$ ，解决流动性市场的最优投资问题；第二步，找到一个最优的非流动性资产投资策略 ${\psi }^{\ast }$ ，使得在模型中达到 $\psi$ 的最大值。

首先考虑固定非流动性资产的投资 $\psi$ 下的最优投资问题。对优化问题进行变换

$\underset{\left(\pi ,\psi \right)\in \mathcal{A}}{\max }\mathbb{E}\left[U\left(Z^{\pi ,\psi }\left(T\right)+\psi F\left(T\right)\right)\right]\equiv \underset{\pi }{\max }\mathbb{E}\left[\tilde{U}\left({\tilde{Z}}^{\pi }\left(T\right)\right)\right].$

其中效用函数 $\tilde{U}(\cdot )$ 定义为 $\tilde{U}\left(\tilde{Z}\right)=U\left(\tilde{Z}+\psi F\left(T\right)\right)$ ，记 ${\tilde{Z}}^{\pi }\left(t\right)\equiv Z^{\pi ,\psi }\left(t\right)$ 是给定非流动性资产投资 $\psi$ 下的流动性盈余过程，同样的 ${\tilde{X}}^{\pi }\left(t\right)\equiv X^{\pi ,\psi }\left(t\right)$ 为给定非流动性资产投资 $\psi$ 下的流动性财富过程，那么有 ${\tilde{Z}}^{\pi }\left(T\right)$ 满足

$\text{d}{\tilde{Z}}^{\pi }\left(t\right)=R{\tilde{Z}}^{\pi }\left(t\right)\text{d}t+\left({\tilde{X}}^{\pi }\left(t\right){\pi }^{\prime }\left(t\right)\text{Σ}+M\left(t\right){\widehat{{\sigma }^{\prime }}}_Y-L\left(t\right){\widehat{{\sigma }^{\prime }}}_l\right)\left(\Xi \text{d}t+\text{d}\mathbb{W}\left(t\right)\right),$ (25)

并且有 ${\tilde{Z}}^{\pi }\left(0\right)={\tilde{X}}^{\pi }\left(0\right)-\psi F\left(0\right)+M\left(0\right)-L\left(0\right)=x_0+m_0-L_0-\psi F\left(0\right)$ 。

现在市场是完备的，接下来我们应用鞅方法来解决最优化问题。将最优化问题化为等价的终端静态问题，以求得最优终端流动性盈余，等价的静态问题为

$\begin{array}{l}\underset{{\tilde{Z}}^{\pi }\left(T\right)}{\max }\mathbb{E}\left[\tilde{U}\left({\tilde{Z}}^{\pi }\left(T\right)\right)\right]\\ \text{s}\text{.t}.\mathbb{E}\left[K\left(T\right){\tilde{Z}}^{\pi }\left(T\right)\right]\le x_0+m_0-L_0-\psi F\left(0\right),\\ {\tilde{Z}}^{\pi }\left(T\right)\ge \alpha .\end{array}$ (26)

为了解决这个问题，本文只考虑当非流动性资产在退休时提供的回报 $F\left(T\right)$ 是一个固定的常数时的情形，我们利用Legendre-Fenchel变换来求解关于点的最大化问题，接下来将进一步解决说明这个问题。

定理3.1 在兼顾非流动性资产投资 $\psi \in \left[0,{\psi }_{\max }\right]$ 和遗产计划 $\alpha \ge 0$ 的情形下，

(i) 损失厌恶型投资者的最优流动性终端盈余为，当 $\theta \ge \psi F\left(T\right)+\alpha$ 时，

${\tilde{Z}}^{{\pi }^{\ast }}\left(T\right)=\{\begin{array}{l}\theta +{\left(\frac{{\gamma }_2}{{\beta }_{1}K\left(T\right)}\right)}^{\frac{1}{1-{\gamma }_2}}-\psi F\left(T\right),K\left(T\right)<\bar{K},\\ \alpha ,K\left(T\right)\ge \bar{K},\end{array}$ (27)

当 $\theta <\psi F\left(T\right)+\alpha$ 时，

${\tilde{Z}}^{{\pi }^{\ast }}\left(T\right)={\left(\theta +{\left(\frac{{\gamma }_2}{{\beta }_{1}K\left(T\right)}\right)}^{\frac{1}{1-{\gamma }_2}}-\psi F\left(T\right)\right)}^{+},$ (28)

其中 $\bar{K}$ 满足条件 $f\left(\bar{K}\right)=0$ ，有

$f\left(x\right)=\left(1-{\gamma }_2\right){\left(\frac{{\gamma }_2}{{\beta }_{1}x}\right)}^{\frac{{\gamma }_2}{1-{\gamma }_2}}+\left(\theta -\psi F\left(T\right)-\alpha \right)\cdot \left[A{\left(\theta -\psi F\left(T\right)-\alpha \right)}^{{\gamma }_1-1}-{\beta }_{1}x\right]$ (29)

且 ${\beta }_1>0$ 为预算约束对应的Lagrange乘数且

$\mathbb{E}\left[K\left(T\right){\tilde{Z}}^{{\pi }^{\ast }}\left(T\right)\right]=x_0+m_0-L_0-\psi F\left(0\right).$

(ii) 已知不同市场环境和基准线下的最优终端流动性盈余，则相应不同情形下的最优终端流动性财富为

${\tilde{X}}^{{\pi }^{\ast }}\left(T\right)={\tilde{Z}}^{{\pi }^{\ast }}\left(T\right)+L\left(T\right).$ (30)

从定理3.1可以得出，当固定非流动性资产的投资 $\psi$ 时，损失厌恶型投资者的最优流动性财富有三种不同的结果，可以看出参考点作为基准线的作用是至关重要的。当 $\theta \ge \psi F\left(T\right)+\alpha$ 时，投资者所面临的参考点高于保障性资产时，投资者将进行对流动性资产的交易来实现目标。当市场状态恶劣时，投资者将做出不购买任何非流动性资产的决定，这时成员的遗产计划和最低生活保障将保护终端财富来给予一个最低的下行保护。当另一种情形 $\theta <\psi F\left(T\right)+\alpha$ 时，保障性资产为投资者提供了足够多的回报，并且投资者将始终实现目标，效用函数从S型退化为CRRA型，这与Desmettre和Seifried [10] 所做的工作是类似的，最优终端总财富 $X_T$ 为

$\begin{array}{l}{\left(\theta +{\left(\frac{{\gamma }_2}{{\beta }_{1}K\left(T\right)}\right)}^{\frac{1}{1-{\gamma }_2}}-\psi F\left(T\right)\right)}^{+}+L\left(T\right)+\psi F\left(T\right)\\ =\left[\theta +{\left(\frac{{\gamma }_2}{{\beta }_{1}K\left(T\right)}\right)}^{\frac{1}{1-{\gamma }_2}}\right]\vee \psi F\left(T\right)+L\left(T\right),\end{array}$ (31)

这与他们在养老金计划前期累积阶段所得的结果一致。

前面的工作已经解决了当非流动性资产投资是一个固定常数时的退休终端财富，接下来我们需要进一步给出确定非流动性资产的最优投资 ${\psi }^{\ast }$ ，并给出流动市场的最优投资策略 ${\pi }^{\ast }$ 的具体显式解。

根据求解思路，进行第二步：找到一个最优的非流动性资产投资策略 ${\psi }^{\ast }$ ，使得在模型中达到 $\psi$ 的最大值。当 $\psi$ 不是一个给定常数时，设 $\psi \in \left[0,{\psi }_{\max }\right]\to ℝ$ ，有

$\begin{array}{c}V\left(\psi \right)=\mathbb{E}\left[\tilde{U}\left({\tilde{Z}}^{{\pi }^{\ast }}\left(T\right)\right)\right]=\mathbb{E}\left[U\left(Z^{{\pi }^{\ast },\psi }\left(T\right)+\psi F\left(T\right)\right)\right]\\ =\underset{\pi :\left(\pi ,\psi \right)\in \mathcal{A}}{\sup }\mathbb{E}\left[U\left(X^{\pi ,\psi }\left(T\right)-L\left(T\right)+\psi F\left(T\right)\right)\right].\end{array}$ (32)

非流动性资产投资的最优策略 ${\psi }^{\ast }$ 由下式给出

${\psi }^{\ast }=\underset{\psi \in \left[0,{\psi }_{\max }\right]}{\arg \max }V\left(\psi \right).$ (33)

在得到投资者的非流动性资产投资的最优策略 ${\psi }^{\ast }$ 后，我们给出此时状态下投资者退休时的最优终端财富。

定理3.2 设 $\mathbb{E}\left[K\left(T\right)Z^{\pi ,\psi }\left(T\right)\right]<\infty$ ， $E\left[U\left(Z^{\pi ,\psi }\left(T\right)\right)\right]<\infty$ ，并且对任意的投资策略 $\left(\pi \left(t\right),\psi \right)\in \mathcal{A}$ ， ${\psi }^{\ast }$ 是使得值函数 $V\left(\psi \right)$ 达到最大的非流动性资产投资策略，则养老金计划投资者的总终端财富

$X^{{\pi }^{\ast },{\psi }^{\ast }}\left(T\right)+{\psi }^{\ast }F\left(T\right),$ (34)

此时投资者的流动性终端财富为

$X^{{\pi }^{\ast },{\psi }^{\ast }}\left(T\right)=\{\begin{array}{ll}\theta +{\left(\frac{{\gamma }_2}{{\beta }_1^{\ast }K\left(T\right)}\right)}^{\frac{1}{1-{\gamma }_2}}-{\psi }^{\ast }F\left(T\right)+L\left(T\right),\hfill & K\left(T\right)<{\bar{K}}^{\ast },\hfill \\ \alpha \cdot {\mathbb{I}}_{\left\{\theta \ge {\psi }^{\ast }F\left(T\right)+\alpha \right\}}+{\left(\theta +{\left(\frac{{\gamma }_2}{{\beta }_1^{\ast }K\left(T\right)}\right)}^{\frac{1}{1-{\gamma }_2}}-{\psi }^{\ast }F\left(T\right)\right)}^{+}\cdot {\mathbb{I}}_{\left\{\theta <{\psi }^{\ast }F\left(T\right)+\alpha \right\}}+L\left(T\right),\hfill & K\left(T\right)\ge {\bar{K}}^{\ast },\hfill \end{array}$ (35)

其中 ${\bar{K}}^{\ast }$ 满足条件 $f\left({\bar{K}}^{\ast }\right)=0$ ，有

$f\left(x\right)=\left(1-{\gamma }_2\right){\left(\frac{{\gamma }_2}{{\beta }_1^{\ast }x}\right)}^{\frac{{\gamma }_2}{1-{\gamma }_2}}+\left(\theta -{\psi }^{\ast }F\left(T\right)-\alpha \right)\cdot \left[A{\left(\theta -{\psi }^{\ast }F\left(T\right)-\alpha \right)}^{{\gamma }_1-1}-{\beta }_1^{\ast }x\right],$ (36)

且 ${\beta }_1^{\ast }>0$ 为预算约束对应的Lagrange乘数且满足

$\mathbb{E}\left[K\left(T\right)Z^{{\pi }^{\ast },{\psi }^{\ast }}\left(T\right)\right]=x_0+m_0-L_0-{\psi }^{\ast }F\left(0\right).$

在确定非流动性资产的最优投资后，我们给出投资者在流动市场中最优投资策略，具体如下。

定理3.3 (i) 当 $\theta \ge {\psi }^{\ast }F\left(T\right)+\alpha$ 时，投资者在时刻 $t\in \left[0,T\right)$ 的最优财富过程为

$\begin{array}{c}{X}^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)=Z^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)-M\left(t\right)+L\left(t\right)\\ =\left(\theta -{\psi }^{\ast }F\left(T\right)-\alpha \right)G\left(t,1\right)\Phi \left(H\left(t,1,{\bar{K}}^{\ast },K\left(t\right)\right)\right)\\ +{\left(\frac{{\gamma }_2}{{\beta }_1^{*}K\left(t\right)}\right)}^{\frac{1}{1-{\gamma }_2}}G\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2}\right)\Phi \left(H\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2},{\bar{K}}^{\ast },K\left(t\right)\right)\right)\\ +\alpha G\left(t,1\right)-M\left(t\right)+L\left(t\right),\end{array}$ (37)

(ii) 当 $\theta <{\psi }^{\ast }F\left(T\right)+\alpha$ 时，投资者在时刻 $t\in \left[0,T\right)$ 的最优财富过程为

$\begin{array}{c}{X}^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)=Z^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)-M\left(t\right)+L\left(t\right)\\ =\left(\theta -{\psi }^{\ast }F\left(T\right)\right)G\left(t,1\right)\Phi \left(H\left(t,1,\kappa \left({\psi }^{\ast }\right),K\left(t\right)\right)\right)\\ +{\left(\frac{{\gamma }_2}{{\beta }_1^{\ast }K\left(t\right)}\right)}^{\frac{1}{1-{\gamma }_2}}G\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2}\right)\Phi \left(H\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2},\kappa \left({\psi }^{\ast }\right),K\left(t\right)\right)\right)-M\left(t\right)+L\left(t\right),\end{array}$ (38)

其中

$G\left(t,b\right)={\text{e}}^{-b\left(R+\frac{1}{2}{\Vert \Xi \Vert }^2\right)\left(T-t\right)+\frac{1}{2}{b}^2{\Vert \Xi \Vert }^2\left(T-t\right)},$ (39)

$H\left(t,b,x,K\left(t\right)\right)=\frac{\ln \frac{x}{K\left(t\right)}+\left(R+\frac{1}{2}{\Vert \Xi \Vert }^2\right)\left(T-t\right)}{\Vert \Xi \Vert \sqrt{T-t}}-b\Vert \Xi \Vert \sqrt{T-t},$ (40)

$\kappa \left({\psi }^{\ast }\right)=\frac{{\gamma }_2}{{\beta }_1^{\ast }{\left(\alpha +{\psi }^{\ast }F\left(T\right)-\theta \right)}^{1-{\gamma }_2}}.$ (41)

这里 $\Phi (\cdot )$ 表示标准正态分布的累积分布函数， ${\bar{K}}^{\ast }$ 和 ${\beta }_1^{\ast }$ 与定理3.2中的定义一致。

定理3.3的证明思路为利用鞅方法求得任意时刻的盈余过程，进而求得最优财富过程。对盈余过程 $Z^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)$ 应用伊藤公式求微分，通过计算和推导得到时刻t在流动市场的最优投资策略。

定理3.4 (i) 当 $\theta \ge {\psi }^{\ast }F\left(T\right)+\alpha$ 时，时刻 $t\in \left[0,T\right)$ 投资者在流动市场最优投资策略为

${\pi }^{\ast }\left(t\right)=\frac{{\Sigma }^{-1}\Xi }{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}\tau \left(t\right)-\frac{{\Sigma }^{-1}{\hat{\sigma }}_Y}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}M\left(t\right)+\frac{{\Sigma }^{-1}{\hat{\sigma }}_l}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}L\left(t\right),$ (42)

故投资于指数债券和股票的财富比例分别为

${\pi }_1^{\ast }\left(t\right)=\frac{{\sigma }_I^{-1}{\xi }_1}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}\tau \left(t\right)-\frac{{\sigma }_I^{-1}{\sigma }_Y{\rho }_{IY}}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}M\left(t\right)+\frac{{\sigma }_I^{-1}{\sigma }_l{\rho }_{Il}}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}L\left(t\right),$ (43)

$\begin{array}{c}{\pi }_2^{\ast }\left(t\right)=\frac{1}{\sqrt{1-{\rho }_{IS}^2}}\frac{-{\sigma }_I^{-1}{\rho }_{IS}{\xi }_1+{\sigma }_S^{-1}{\xi }_2}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}\tau \left(t\right)\\ -\frac{1}{\sqrt{1-{\rho }_{IS}^2}}\frac{-{\sigma }_I^{-1}{\rho }_{IS}{\sigma }_Y{\rho }_{IY}+{\sigma }_S^{-1}{\sigma }_Y\sqrt{1-{\rho }_{IY}^2}}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}M\left(t\right)\\ +\frac{1}{\sqrt{1-{\rho }_{IS}^2}}\frac{-{\sigma }_I^{-1}{\rho }_{IS}{\sigma }_l{\rho }_{Il}+{\sigma }_S^{-1}{\sigma }_l\sqrt{1-{\rho }_{Il}^2}}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}L\left(t\right),\end{array}$ (44)

其中

$\begin{array}{c}\tau \left(t\right)=\frac{\left(\theta -{\psi }^{\ast }F\left(T\right)-\alpha \right)}{\Vert \Xi \Vert \sqrt{T-t}}G\left(t,1\right)\varphi \left(H\left(t,1,{\bar{K}}^{\ast },K\left(t\right)\right)\right)\\ +{\left(\frac{{\gamma }_2}{{\beta }_1^{\ast }K\left(t\right)}\right)}^{\frac{1}{1-{\gamma }_2}}G\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2}\right)\left(\frac{\Phi \left(H\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2},{\bar{K}}^{\ast },K\left(t\right)\right)\right)}{1-{\gamma }_2}+\frac{\varphi \left(H\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2},{\bar{K}}^{\ast },K\left(t\right)\right)\right)}{\Vert \Xi \Vert \sqrt{T-t}}\right).\end{array}$ (45)

(ii) 当 $\theta <{\psi }^{\ast }F\left(T\right)+\alpha$ 时，时刻 $t\in \left[0,T\right)$ 投资者在流动市场最优投资策略为

${\pi }^{\ast }\left(t\right)=\frac{{\Sigma }^{-1}\Xi }{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}\tilde{\tau }\left(t\right)-\frac{{\Sigma }^{-1}{\hat{\sigma }}_Y}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}M\left(t\right)+\frac{{\Sigma }^{-1}{\hat{\sigma }}_l}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}L\left(t\right),$

故投资于指数债券和股票的财富比例分别为

${\pi }_1^{\ast }\left(t\right)=\frac{{\sigma }_I^{-1}{\xi }_1}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}\tilde{\tau }\left(t\right)-\frac{{\sigma }_I^{-1}{\sigma }_Y{\rho }_{IY}}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}M\left(t\right)+\frac{{\sigma }_I^{-1}{\sigma }_l{\rho }_{Il}}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}L\left(t\right),$ (46)

$\begin{array}{c}{\pi }_2^{\ast }\left(t\right)=\frac{1}{\sqrt{1-{\rho }_{IS}^2}}\frac{-{\sigma }_I^{-1}{\rho }_{IS}{\xi }_1+{\sigma }_S^{-1}{\xi }_2}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}\tilde{\tau }\left(t\right)\\ -\frac{1}{\sqrt{1-{\rho }_{IS}^2}}\frac{-{\sigma }_I^{-1}{\rho }_{IS}{\sigma }_Y{\rho }_{IY}+{\sigma }_S^{-1}{\sigma }_Y\sqrt{1-{\rho }_{IY}^2}}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}M\left(t\right)\\ +\frac{1}{\sqrt{1-{\rho }_{IS}^2}}\frac{-{\sigma }_I^{-1}{\rho }_{IS}{\sigma }_l{\rho }_{Il}+{\sigma }_S^{-1}{\sigma }_l\sqrt{1-{\rho }_{Il}^2}}{X^{{\pi }^{\ast },{\psi }^{\ast }}\left(t\right)}L\left(t\right),\end{array}$ (47)

其中

$\begin{array}{c}\tilde{\tau }\left(t\right)=\frac{\theta -{\psi }^{\ast }F\left(T\right)}{\Vert \Xi \Vert \sqrt{T-t}}G\left(t,1\right)\varphi \left(H\left(t,1,\kappa \left({\psi }^{\ast }\right),K\left(t\right)\right)\right)\\ +{\left(\frac{{\gamma }_2}{{\beta }_1^{\ast }K\left(t\right)}\right)}^{\frac{1}{1-{\gamma }_2}}G\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2}\right)\left(\frac{\Phi \left(H\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2},\kappa \left({\psi }^{\ast }\right),K\left(t\right)\right)\right)}{1-{\gamma }_2}+\frac{\varphi \left(H\left(t,\frac{-{\gamma }_2}{1-{\gamma }_2},\kappa \left({\psi }^{\ast }\right),K\left(t\right)\right)\right)}{\Vert \Xi \Vert \sqrt{T-t}}\right),\end{array}$ (48)

这里 $\kappa \left({\psi }^{\ast }\right)$ 的定义在定理3.3中已给定。

注3.1 当 $\theta <{\psi }^{\ast }F\left(T\right)+\alpha$ 时，此时保障性资产为投资者提供了足够多的回报，投资者始终实现目标，效用函数由S型退化成CRRA型，这时设定参考点 $\theta =0$ ，同时我们不考虑人力资本 $M\left(t\right)$ 和最低生活保障 $L\left(t\right)$ 对财富的影响，这时可以得到和Desmettre和Seifried [10] 相同的结果，因此在第4节数值模拟，我们只关注 $\theta \ge {\psi }^{\ast }F\left(T\right)+\alpha$ 情形下的一些特征对投资策略的影响。

4. 数值模拟

本节我们将得到一些数字结论来分析非流动性对投资组合选择的影响、模型参数及特征对投资策略的影响，基于这些模拟结果，提供相应的经济解释。

首先进行一些参数的设定。假设实际回报率 $r=0.02$ ，名义收益率 $R=0.05$ ，各类增长率和波动率分别为 ${\mu }_I=0.033$ ， ${\mu }_S=0.065$ ， ${\mu }_Y=0.1$ ， ${\mu }_l=0.1$ 和 ${\sigma }_I=0.2$ ， ${\sigma }_S=0.4$ ， ${\sigma }_Y=0.25$ ， ${\sigma }_l=0.36$ 。相关系数分别为 ${\rho }_{IS}=0.5$ 、 ${\rho }_{IY}=0.6$ ， ${\rho }_{Il}=0.55$ 。可计算出市场风险价格 ${\xi }_1=0.015$ ， ${\xi }_2=0.035$ 。

对于DC型养老金计划参与成员，退休年龄 $T=55$ ，死亡年龄 $\bar{T}=75$ ，初始总财富为 $x_0=10$ ，初始工资为 $y_0=0.4$ ，缴费率 $c=8\%$ ，初始人力资本价值 $m_0=\frac{1}{{\tau }_1}\left({\text{e}}^{{\tau }_1\left(T-t\right)}-1\right)c{y}_0=7$ ，基于上述设定假设 $l_0=1$ ，非流动性资产投资约束 ${\psi }_{\max }=8$ ，考虑成员有遗产计划 $\alpha =20$ 。为了后续分析，我们应用蒙特卡洛方法模拟了 $l\left(t\right)$ 的2000条路径，再求平均值作为 $l\left(t\right)$ 的运动轨迹，最后求出相应终端 $L\left(T\right)$ 。

对于效用函数参数，设 ${\gamma }_1=0.15$ 、 ${\gamma }_2=0.2$ 、 $A=2.25$ ，参考点在后续分析中有不同设定。

4.1. 非流动性资产投资对终端总财富的影响

“图1”显示了当对非流动性资产投资存在不同决策时，对投资选择的影响。如“图1”所示，养老金投资者对非流动性资产的投资有助于对冲流动性组合资产的风险，当随机贴现因子 $K\left(T\right)$ 越高时，市场的环境相对更加恶劣，这时即使在市场不好的状态下，非流动性资产也能对财富提供一个较低限度的保障 $\psi F\left(T\right)$ ，也就是意味着投资者的流动性交易市场恶化，他们需要通过购买非流动性资产来获得财富保障，并且更高的回报率会增加投资者非流动性资产的购买力。在不购买任何非流动性资产的情况下，成员的遗产计划和退休后的最低生活保障会给财富制定一个最低基准。当随机贴现因子较低时，市场相对繁荣，投资者面临一个良好的投资环境，这时主要通过购买流动性组合资产获得更高的收益。

4.2. 人力资本贡献初值对投资策略的影响

“图2”显示了当 $t=0$ 时在不同非流动性资产投资决策下，不同的人力资本贡献初值对股票最优投资策略的影响。当劳动收入越高时，成员退休时的养老金就越高，相应的缴费随之增加，那么成员未来预期贡献也就越高。观察三条曲线，发现当增加人力资本未来预期贡献的累积贴现值，将会降低对股票的投资比例。较低的 $m_0$ ，投资者处于亏损的状态，这时损失厌恶的投资者会寻求风险，加大对高增长潜力的股票的投资来获得更多的收益。当 $m_0$ 越高时，成员的养老金账户收到的预期缴费越高，这时他会减少对股票的投资来降低风险。当投资者不购买任何非流动性资产时(点虚线)，投资者将会加大对流动性资产的投资以此获得的收益。购买较多的非流动性资产后(实线)，投资者会降低对股票的投资来保护自己的风险承受能力。

Figure 1. Effect of trading in illiquid assets on the total terminal wealth ( $\theta =350$ )

图1. 非流动性资产的交易对终端总财富的影响( $\theta =350$ )

Figure 2. Effect of initial human capital contribution under different trading on the optimal strategy for the stock ( $\theta =50$ )

图2. 人力资本贡献初值对(股票)投资策略的影响( $\theta =50$ )

4.3. 财富初值对投资策略的影响

“图3”显示了当 $t=0$ 时在不同非流动性资产投资决策下，不同的财富初值对股票最优投资策略的影响。从图中虚线和实线的走势，随着初始财富的增加，投资者会增加对股票的投资比例，这是因为较高的初始财富，对于厌恶损失的投资者来说，可能会选择风险更高的投资策略，以此获得更高的回报。但当投资者面临着较高的投资风险时，如图所示股票投资比例的上升速度变得缓和，这时他会通过减缓对投资的增加来降低风险。当投资者投入较多财富来购买非流动性资产(实线)时，非流动性资产带来的收益会增加投资者的投资热情。

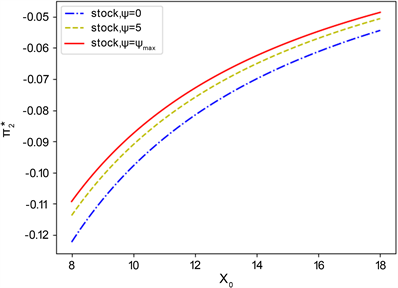
Figure 3. Effect of initial wealth under different trading on the optimal strategy for the stock ( $\theta =100$ )

图3. 财富初值对(股票)投资策略的影响( $\theta =100$ )

4.4. 退休年限对投资策略的影响

“图4”显示了当 $t=0$ 时在不同非流动性资产投资决策下，成员的不同退休年限对股票最优投资策略的影响。成员的退休年限决定了投资者的投资期限，随着成员退休年龄的推延，人力资本的累积会逐渐增加，这时投资者对股票的投资比例首先会随着投资年限T的增加而降低，考虑到自己的风险承受能力，此时会降低风险资产的投资来获得稳定的收益。但由于成员在退休前积累的财富，在退休后需依靠这些财富来维持生活，那么在一定年限后，投资者需考虑平衡累积和投资，这时会愿意承担更大的风险，加大对股票的投资比例，获得更多的收益，为后续的退休生活提供更多的保障。观察点虚线，当投资年限较低时，相较存在非流动性资产的交易，不购买非流动性资产的投资者将会加大对股票的投资比例，因为此时人力资本的回报较减少对风险资产的投资，降低风险，对资产进行下行保护。

4.5. 遗产计划对投资策略的影响

“图5”显示了当 $t=0$ 时，计划成员存在 $\psi =5$ 头寸的非流动性资产的交易下，不同的遗产计划对股票最优投资策略的影响。观察虚线和实线，当成员有遗产计划需求时，投资者对股票的投资比例会随着投资期限的增加而减少。进一步分析，当遗产计划的拥有量较高时，前期投资者对股票的投资不做较大幅度的调整，当投资年限延长到较大值时，账户中的财富已经累积到可观数额，这时投资者会明显减少对股票的投资，从而降低风险。对比点虚线，当遗产计划的拥有量较低时，投资者在前期会投入一定资产购买股票以此获得收益，但随着后期投资年限的增加，会降低股票的投资比例，对资产持有量做出保护。观察点虚线，对于没有遗产计划的成员，为了减少风险避免损失，投资者将对资金的分配不做大幅度的调整。

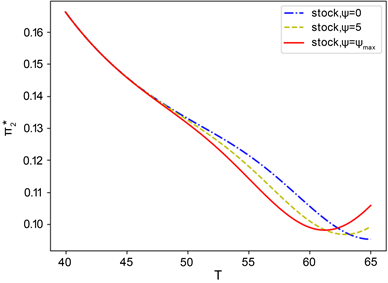
Figure 4. Effect of length of retirement under different trading on the optimal strategy for the stock ( $\theta =100$ )

图4. 退休年限对(股票)投资策略的影响( $\theta =100$ )

Figure 5. Effect of estate planning on the optimal strategy for the stock ( $\theta =200$ )

图5. 遗产计划对(股票)投资策略的影响( $\theta =200$ )

5. 结论

本文研究了当存在非流动性资产的交易，并且涉及养老金计划参与者的遗产计划、退休前的随机劳动工资、退休后的生活保障和通货膨胀的风险时，损失厌恶的养老金计划参与者的最优投资组合问题。在S型效用函数的作用下，根据Legendre-Fenchel变换求出养老金在不同市场环境和基准线下分为三种情形进行求解，得到最优终端流动性盈余和财富，在确定非流动性资产的最优投资策略后，相应地给出最优终端总财富。然后运用鞅方法得到在基准线划分下，两种不同情形的最优投资组合策略和财富过程。最后进行数值模拟发现对非流动性资产的投资有助于对冲流动性组合资产的风险，并且退休时非流动性资产的回报和遗产计划同样担任着对财富的最低限度保障。并且发现当存在不同非流动性资产交易时，人力资本贡献初值、财富初值、退休年限对投资策略会产生一定的影响，需要根据实际情况平衡收益和风险。最后当存在不同的遗产计划需求时，投资者会对投资做出减少或不做较大调整的决策。本文在前期工作者的基础上，考虑了存在遗产计划需求和退休后的分配工作进行一些结果的讨论，同时对非流动性资产的随机性和允许财富进行一些借贷交易，可进行下一步工作的讨论。

致谢

感谢国家自然科学基金资助项目(12061066)；甘肃省自然科学基金(20JR5RA528)给予资金的支持。

NOTES

^*通讯作者。