垂直管环状流场中液滴夹带率预测新模型

A New Model for Predicting Droplet Entrainment Rate in Vertical Tube Annular Flow Field

摘要: 液滴夹带率是认识环状流典型特征的重要参数之一，对其准确预测对于揭示环状流场中液膜厚度、液体携带形式，以及计算压降梯度均具有重要意义。现有液滴夹带率预测方法以经验公式为主，通过实验数据拟合得到，其适用条件有限。本章收集了更宽泛的液体种类、液流速、气流速、实验压力、管径的实验数据共785组，在其基础之上建立了环状流液滴夹带率预测了新模型，该模型是对Cioncolini和Thome (2012)所建关系式形式的发展。新模型考虑了气流速、液流速、压力、气体密度、气体粘度和管径的影响。新模型与现有14个模型相比，准确性更高，适用的参数范围更宽。

Abstract: Droplet entrainment rate is one of the important parameters to understand the typical characteris-tics of annular flow, and its accurate prediction is of great significance to reveal the thickness of liq-uid film, the form of liquid carriage and the calculation of pressure drop gradient in annular flow field. The existing prediction methods of droplet entrained rate are mainly based on empirical for-mulas, which are obtained by fitting experimental data, and their application conditions are lim-ited. In this chapter, 785 sets of experimental data on a wider range of liquid types, liquid flow rate, gas flow rate, experimental pressure and pipe diameter were collected, on which a new model for predicting droplet entrainment rate of annular flow was established. This model is an evolution of the form of the relationships established by Cioncolini and Thome (2012). The new model takes into account the effects of gas flow rate, liquid flow rate, pressure, gas density, gas viscosity and pipe diameter. Compared with the existing 14 models, the new model has higher accuracy and wider range of applicable parameters.

1. 引言

液滴夹带率是认识环状流典型特征的重要参数之一，对其准确预测对于揭示环状流场中液膜厚度、液体携带形式，以及计算压降梯度均具有重要意义。

目前，众多学者提出了许多液滴夹带率公式，如表1所示。在这些公式中，普遍使用了韦伯数这一特征参数。韦伯数是气流的动力与液滴的界面张力之比，韦伯数越大，表示气流破碎液体的能力越强，液滴夹带率越高。Paleev & Filippovich [1] 最早利用韦伯数等无因次数作为判定标准，提出了液滴夹带率公式。公式中使用了气芯密度，而气芯密度与液滴夹带率有关，因此液滴夹带率计算需要迭代求解，使用不很方便。随后，Wallis [2] 使用气体密度代替气芯密度，简化了Paleev & Filippovich公式。Paleev & Filippovich公式和Wallis公式均没有考虑液流速的影响，有一定局限性。随后Oliemans等人 [3] 考虑了气、液物性质和管径的影响，在对Harwell数据库进行回归分析后，提出了液滴夹带率预测新方法，关系式中虽然没有使用气体韦伯数的概念，但之后Zhang等人 [4] 在Oliemans公式中重新引入了气体韦伯数。

Ishii & Mishima [5] 认为是液膜表面的扰动波在气流剪切作用下破碎产生液滴。基于这一机理，他们提出了液滴夹带率预测新关系式。该关系式使用了修正气体韦伯数(在气体韦伯数中引入(Δρ/ρ_g)^1/3)以拟合不同压力下的数据。之后，Utsono & Kaminanga [6] 使用3~9 MPa的高压水蒸汽/空气数据分析了Ishii & Mishima公式，结果发现该公式在高压条件下误差较大，这可能是因为高压条件下的液滴夹带机理有所不同，而Ishii & Mishima的实验数据是在低压条件下得出的。由此，Utsono & Kaminanga使用高压水蒸汽/空气数据修正了Ishii & Mishima公式，但是这一公式并不适用于低压条件的液滴夹带率预测。

Sawant等人 [7] 根据实验数据进一步修正了Ishii & Mishima的修正韦伯数(将(Δρ/ρ_g)的指数由1/3改为1/4)，并与液相雷诺数一起对液滴夹带率进行了拟合。同时，他们认为即使在气流速很高的情况下，液膜也不可能全部形成液滴，即F_E的极限值小于1。由此他们的公式中引入了最大(极限)液滴夹带率。不过在确定最大液滴夹带率时，由于数据库的限制，他们只提出了一个简单的经验关系式。之后，Sawant等人 [8] 利用大量数据进一步完善了最大(极限)液滴夹带率的经验关系式。

Table 1. Existing formula for calculating friction coefficient of gas-liquid interface

表1. 现有的气液界面摩擦系数计算公式

Cioncolini & Thome [9] 分析液滴夹带率时，既没有使用韦伯数也没有使用Ishii & Mishima和Sawant等人提出的两种修正韦伯数，而是分析了液滴夹带率与气芯韦伯数的关系，他们发现气芯韦伯数与液滴夹带率存在着一种S形趋势，并使用Logistic函数拟合这种S形函数关系。但是，气芯韦伯数的计算既需要液滴夹带率也需要液膜厚度，整个计算过程较为复杂，而且他们的数据库集中在F_E < 0.5区域，F_E > 0.5区域的数据较少。总体而言，数据发散较为严重。之后Cioncolini & Thome [10] 扩大了之前的环状两相流实验数据库，清除了许多被视为异常值的数据点。同时为了公式在工程中便于应用，他们简化了之前的气芯韦伯数计算公式，重新拟合公式中的参数，并提出的一个显式的预测校正方案，但是气芯韦伯数与液滴夹带率的关系仍然是一条单一的曲线，数据发散严重。

与其他学者不同，Berna等人 [11] 根据液滴平均直径的计算推导了液滴夹带率公式。整个公式的形式和Zhang公式相似，不过他们使用Sawant等人的修正韦伯数代替了韦伯数，同时他们引入了Ishii & Mishima提出的C_W。该公式误差较大，而且许多计算值呈现出与实验值相反的趋势。Aliyu等人 [12] 也使用修正韦伯数代替了和Zhang公式中的韦伯数，此外还去除了气液密度比和气液粘度比两项。同时发现，高气流速下，液滴夹带率与气体雷诺数的相关性较弱，他们认为在表观气流速大于40 m/s时，气体流量的增加并不会导致气芯中液滴夹带率的显著增加，因此在该情况下忽略了气体雷诺数的影响。

本文利用大量的实验数据对以上的液滴夹带率公式进行了评价，评价结果如图5所示。由图5评价结果可知，这些根据低压数据推导的液滴夹带率公式在预测高压工况下的液滴夹带率时存在较大的误差，同时高压情况下的公式也不适用于低压条件。总体而言，这些液滴夹带率公式在较宽泛的实验数据范围内表现较差，准确性不高。

2. 文献中的实验数据

本文共收集了16篇文献中总计785个垂直管环状流的实验数据点。它们涵盖了广泛实验工况，其中表观液流速0.0035~1 m/s、表观气流速0.8~120 m/s、测试压力1~200 bara和管径5~127 mm。关于数据库中各项实验的详细实验工况如表2所示。

在这785个数据点中，Fore & Dukler的实验中使用了水和50%甘油水溶液两种工作液体，它们的运动粘度分别为1 cP和6 cP。Asali的实验中使用了水和甘油水溶液两种工作液体，它们的运动粘度分别为1.1 cP和2.59 cP。Lopez de Bertodano等人的实验中使用的工作液体是Freon-113，当系统压力为0.5 MPa时，其物理性质为：表面张力0.01085 N/m，ρ_l/ρ_g为40.9，μ_l/μ_g为23.65。除了以上数据之外，数据库中的大部分测量数据来自大气压下的空气/水两相流。

图1所采用的流型过渡边界来自Hewitt和Roberts。基于大量数据，他们以气相和液相的流动通量为坐标，给出了一种的流型分布图。将数据库中的785个数据点绘制到该流型分布图中，可以发现，本文所选取的所有数据点都位于环状流区域。

Table 2. The experimental conditions of each experiment

表2. 各项实验的实验工况

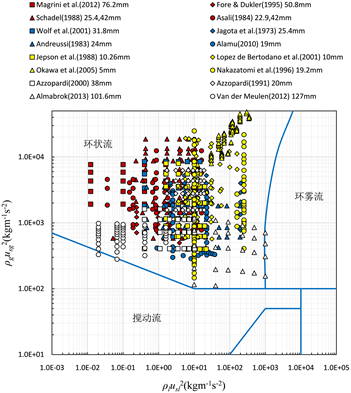
Figure 1. Distribution of experimental data on Hewitt and Roberts flow patterns

图1. 实验数据在Hewitt和Roberts流型图上的分布

3. 新的液滴夹带率计算公式

3.1. 液滴夹带率新公式的形式

对现有的液滴夹带率公式进行了评价，由图2和表3可知，现有的液滴夹带率公式中预测情况最好的是Cioncolini和Thome的经验公式，但是该经验公式在形式上依然是一条液滴夹带率和气芯韦伯数的单一曲线，如图2所示，数据的分散依然严重。严重分散的主要是Nakazatomi等人的高压数据和Van der Meulen等人的大管径数据。对于Nakazatomi等人的高压下的空气/水数据的误差较大，这是因为Cioncolini和Thome在拟合数据时，将这类数据视为异常点进行了剔除。同时由于数据库的限制，他们对于大于100 mm管径的高液滴夹带率的预测误差较大。

Figure 2. The relationship between droplet entrainment rate and gas core Weber number

图2. 液滴夹带率和气芯韦伯数的关系

本文在Cioncolini和Thome公式的基础上进行了修正。首先，使用修正气体韦伯数、液体韦伯数和液体粘度比替换了Cioncolini和Thome公式中的气芯韦伯数，将原本的隐式公式变为了显式公式，去除了迭代过程。修正气体韦伯数、液体韦伯数和液体粘度比考虑了管径、气流速、气体密度、液流速、液体粘度和表面张力等液滴夹带率的主要影响因素。其中修正气体韦伯数和液体韦伯数如式(1)和式(2)所示：

$W{e^{\prime }}_g=\frac{{\rho }_g{u}_{sg}^{2}D}{\sigma }{\left(\frac{\Delta \rho }{{\rho }_g}\right)}^{1/4}$ (1)

式中： $W{e^{\prime }}_g$ 为修正气体韦伯数；ρ_g为气体密度，kg/m³；u_sg为气体表观流速，m/s。D为管径，m；σ为界面张力，N/m；Δρ为气液密度差，kg/m³。

$W{e}_l=\frac{{\rho }_l{u}_{sl}^{2}D}{\sigma }$ (2)

式中：We_l为液体韦伯数；ρ_l为液体密度，kg/m³；u_sl为液体表观流速，m/s。

所以液滴夹带率的新公式形式如下：

$F_E={\left(1+aW{e^{\prime }}_g^{b}W{e}_l^c{\left(\frac{{\mu }_l}{{\mu }_w}\right)}^d\right)}^f$ (3)

式中：F_E为液滴夹带率，无因次；μ_l为液体的运动粘度，mPa·s；μ_w为20℃时水的运动粘度，mPa·s。

3.2. 低压下的液滴夹带率新公式

根据低压实验数据的分析，随着液气比、气体密度和管径的增大，液滴夹带率增大。而在公式评价中我们发现许多公式都过度预测了20 mm管径以下的小管径数据，同时低估了大于100 mm的大直径管道的较大的液滴夹带率。管径大于100 mm的管道都有着较大的液滴夹带率，这可能是因为增大的气芯空间使液滴更不可能重新沉积。这与Azzopardi等人的观察结果一致，Azzopardi等人在较大的管道中观察到了不同的扰动波特性。这些扰动波长期以来一直被认为是液滴的来源，液滴被剪切到气体气芯。所以本文以20 mm和100 mm为分界线提出了对3个管径区域开发不同的计算公式。

利用麦夸特法 + 通用全局变量法和整个实验数据库中压力小于2 MPa的数据确定了系数a和这些指数，得到新的液滴夹带率公式如下：

$F_E={\left(1+320W{e^{\prime }}_g^{-0.065}W{e}_l^{-0.057}{\left(\frac{{\mu }_l}{{\mu }_w}\right)}^{0.049}\right)}^{-2.89}$ 管径 < 20 mm (4)

$F_E={\left(1+282W{e^{\prime }}_g^{-0.625}W{e}_l^{-0.267}{\left(\frac{{\mu }_l}{{\mu }_w}\right)}^{0.287}\right)}^{-1.129}$ 20 mm < 管径 < 100 mm (5)

3.3. 高压下的液滴夹带率新公式

而本文关注的是井筒的积液问题，而非核反应堆中的传热问题，所以本文使用了高压下的Nakazatomi等人的空气/水数据，而非高温高压下的Adamsson & Anglart和Würtz的空气/水蒸汽数据。由此，利用Nakazatomi等人的数据和式(1)绘制了图3。由图3可知，式(1)并不能很好的拟合Nakazatomi等人的数据中压力大于2 MPa时的液滴夹带率数据。这可能是因为高压区域中液滴夹带的机理与低压区域不同。

Figure 3. Droplet entrainment rate vs $W{e^{\prime }}_c^{0.765}W{e}_l^{0.057}{\left({\mu }_l/{\mu }_w\right)}^{-0.049}$

图3. 液滴夹带率vs $W{e^{\prime }}_c^{0.765}W{e}_l^{0.057}{\left({\mu }_l/{\mu }_w\right)}^{-0.049}$

为了适应高压条件下的实验数据，本文在高压区域的公式中加入了一个有关压力的无因次变量，以加大对压力因素的考虑。利用麦夸特法 + 通用全局变量法和Nakazatomi等人的高压数据(P > 2 MPa)确定了系数a和这些指数，得到高压情况下新的液滴夹带率公式如下：

$F_E={\left(1+453401W{e^{\prime }}_g^{-0.67}W{e}_l^{-0.22}{\left(\frac{{\mu }_l}{{\mu }_w}\right)}^{0.049}{\left(\frac{P}{0.101}\right)}^{-1.82}\right)}^{-1.537}$ (6)

式中：P为系统压力，MPa。

由图4可知，压力大于2 MPa的高压数据和压力小于2 MPa的低压数据明显处于两个不同的区域，这也证明了本文以2 MPa为界限的正确性。

Figure 4. Droplet entrainment rate vs $W{e^{\prime }}_c^{0.67}W{e}_l^{0.22}{\left({\mu }_l/{\mu }_w\right)}^{-0.049}{\left(P/0.101\right)}^{1.82}$

图4. 液滴夹带率vs $W{e^{\prime }}_c^{0.67}W{e}_l^{0.22}{\left({\mu }_l/{\mu }_w\right)}^{-0.049}{\left(P/0.101\right)}^{1.82}$

4. 液滴夹带率公式的评价

液滴夹带率实验值与现有计算公式以及新的液滴夹带率公式的计算值对比如图5所示。从图5可以看出，现有的模型并不能很好地计算所有数据点的液滴夹带率。如图5(a)~(n)所示，Aliyu等人的公式重点考虑了大管径下液滴夹带率计算，却过度预测了Jepson等人和Alamu等人的小管径的液滴夹带率。Paleev & Filippovich公式对数据库中的数据普遍存在着过度预测的情况，甚至很多F_E值都大于1。相比之下，它的简化形式的Wallis公式产生的发散要少一些，但是总体误差依然较大，尤其是F_E < 0.5时。与Paleev & Filippovich公式相反，Ishii & Mishima公式则是低估了数据库中的大部分数据，尤其是Nakazatomi等人的高压数据。Oliemans公式和Zhang等人的公式低估了Nakazatomi等人的高压数据，又过度预测了Jepson等人、Alamu等人和Lopez de Bertodano等人的小管径数据，但有趣的是它对Okawa等人的5mm管径数据的预测又很好。Utsono & Kaminanga公式在预测本文数据库时，因为大部分数据均不在其适用条件3~9 MPa中，所以出现预测值为负的情况。Petalas & Aziz公式无法预测F_E小于0.5的情况，它的大多数预测值都集中在0.8以上，并有许多较大的偏差。Pan & Hanratty公式明显低估了Nakazatomi等人的高压数据。Sawant等人的两个公式也都低估了Nakazatomi等人的高压数据，值得注意的是，他们提出最大液膜雷诺数最初随着表观液体雷诺数的增加而增加，在较高的液体雷诺数处渐近于一个恒定值，但他们建模时使用对数方程。而对数方程呈现的是速率递减特性，而不是渐进特性。所以Sawant公式(2008)在低表观液体雷诺数时存在一个问题，即最大夹带率大于1。Sawant公式(2009)也存在两个主要问题：1) 即使对于非常大的表观液体雷诺数，其渐近值始终在0.8左右；2) 当 $R{e}_{sl}-13N_{\mu f}^{-0.5}$ 为负，也就是液体流速较低时，数值计算结果无效。这种关系式只适用于环雾流，而且该关系式在预测蒸汽/水的数据时误差较大。Cioncolini和Thome的两个公式是现有公式中预测情况最好的，但是它们同样无法较好的预测Nakazatomi等人的高压数据。Berna公式低估了Nakazatomi等人的高压数据和Lopez de Bertodano等人的数据，其他情况下，它的预测值都太大。几乎所有现有公式都低估了高压情况下的数据，Utsono & Kaminanga公式虽然是针对高压情况提出的，但是它的预测情况同样不好，这是它们的实验条件并没有覆盖这些区域。从图5(o)可以看出，新公式比图5(a)~(n)中的任何一种公式都更符合数据。

统计数据(均方误差、平均绝对误差等)也表明，所提出的新相关性可以很好地计算当前数据。它有着最低的均方误差(MSE)和平均绝对误差(MAE) (见表3)。Paleev & Filippovich，Utsono & Kaminanga，Berna等人，Petalas和Aziz的公式误差太大，平均绝对误差(>100%)，而且较少计算值在±50%误差范围(<50%)。相比之下，其他公式虽有所改善，但平均绝对误差仍然>50%。在这些现有的模型中，Cioncolini和Thome的两个公式的均方误差(MSE)最小，超过70%的计算值在±50%的误差范围内。但是从图5(m)和图5(n)中可以看出，通过这两种公式同样无法较好的预测Nakazatomi等人的高压数据。而新的公式则可以更好地计算液滴夹带率，尤其是高压情况下的液滴夹带率。

Figure 5. Comparison of experimental values of droplet entraining rate with those calculated by various formulas

图5. 液滴夹带率实验值与各种公式计算值的比较

Table 3. Error statistics between the new formula and the existing formula

表3. 新公式和现有的公式之间的误差统计

平均绝对误差百分比

(7)

均方误差

$\frac{1}{n}{{{\displaystyle \sum }}^{\text{}}}_i^n{\left(F_{E,实验值}-F_{E,计算值}\right)}^2$ (8)

5. 结论

(1) 使用气体韦伯数、液体韦伯数和液体粘度比替代了Cioncolini和Thome公式中需要迭代计算的气芯韦伯数。

(2) 考虑到管道直径对液滴夹带率的影响，以20 mm和100 mm为界限，将管径分为3个区域，提出了不同的液滴夹带率公式。

(3) 因为高压条件下液滴夹带的机理不同，对于压力大于2 MPa的情况，提出了不同的液滴夹带率公式。

(4) 新公式对所有数据点的平均绝对百分误差为20.02%。与其它模型相比，新公式计算精度最好。