基于二维卷积神经网络的轴承故障智能诊断

Intelligent Diagnosis of Bearing Faults Based on Two-Dimensional Convolutional Neural Network

摘要: 机械故障诊断已成为保证设备安全稳定运行的重要手段和关键技术之一。机械故障诊断对于保障设备安全运行意义重大，然而传统诊断方法太过依赖专家经验和先验知识，一直是该领域亟需解决的问题。随着机器学习的诞生和发展，基于深度学习的智能诊断方法应运而生。本文提出一种以短时傅里叶变换时频图为输入的二维卷积神经网络架构，在结构并不复杂的前提下可以实现轴承故障“端到端”的智能诊断。使用凯斯西储大学轴承故障数据集进行验证，结果表明所提方法具备有效性，且优于对比方法。总结整体方法流程并给出结论。

Abstract: Mechanical fault diagnosis has become one of the important means and key technologies to ensure the safe and stable operation of equipment. Mechanical fault diagnosis is of great significance to ensure the safe operation of equipment, however, traditional diagnostic methods rely too much on experts’ experience and a priori knowledge, which has been an urgent problem in this field. With the birth and development of machine learning, intelligent diagnosis methods based on deep learning have emerged. In this paper, we propose a two-dimensional convolutional neural network architecture with short-time Fourier transform time-frequency images as inputs, which can realize “end-to-end” intelligent diagnosis of bearing faults under the premise of uncomplicated structure. Validation using the Case Western Reserve University bearing failure dataset shows that the pro-posed method is effective and outperforms the comparison method. Summarize the overall method process and provide conclusions.

1. 引言

制造业既是国民经济发展中的关键产业，又对于国防建设起到不可或缺的作用。在制造业实际生产运作中，各种机械设备会面临重载、疲劳、腐蚀、高温等复杂恶劣的工作环境，这些因素的综合作用将导致核心零部件和关键机械结构发生故障。一旦发生机械故障，轻则造成生产中断、经济损失，重则导致安全事故、危及生命。因此，对于机械设备进行故障诊断，既可以确保设备稳定运转、降低维护成本，又能够及时排查隐患、降低安全风险。

轴承是现代机械设备中的一种关键零部件，被广泛应用于航天、风电、汽车、矿山机械等领域，也是机械故障诊断研究的重点关注对象。传统故障诊断方法需要人工提取特征的过程依赖于专家经验和先验知识，不仅费时费力，而且具有较高的使用门槛。因此，越来越多的研究人员将目光汇聚在近年来逐渐兴起的机器学习、深度学习方法上，广泛采用神经网络等算法进行轴承故障智能诊断。2020年，何宗博 [1] 等学者使用一维空洞卷积模型直接对原始信号进行自动提取特征、故障分类，结果表明该模型可有效识别轴承故障。魏乐 [2] 等学者采用高斯–伯努利受限玻尔兹曼机模型对深度信念网络进行改进，取得了更好的分类效果、更快的收敛速度。2021年，张训杰 [3] 等学者通过格拉姆角场(GAF)输出图像，保留了丰富的信号信息，再输入到卷积神经网络结合双向门控循环单元模型进行识别。田科位 [4] 等学者将挤压与激励网络结构应用于改进深度残差网络，实验结果表明该方法诊断能力良好。2022年，瞿红春 [5] 等学者利用注意力循环机制构建数字胶囊，进而提出融合胶囊网络模型，通过实验证实了其用于轴承故障诊断的有效性和泛化性。李魁 [6] 等学者利用变分模态分解将信号分解成多个模态分量，最优模态分量输入卷积神经网络进行诊断。2023年，聂磊 [7] 等学者构造相似度特征并经筛选后融合，构建健康指标后输入卷积神经网络实现了轴承剩余寿命预测。武煜坤 [8] 等学者将格拉姆角场输出的特征图输入到G-YOLO模型进行诊断，经实验证明了所提方法的有效性。

根据基于深度学习方法的轴承故障诊断研究现状，本文进行基于二维卷积神经网络的轴承故障智能诊断研究。首先，考虑原始振动信号在时频域上特征分布相较时域更加详细丰富，利用短时傅里叶变换(Short-time Fourier Transform, STFT)将轴承一维振动信号进行处理后，输出为二维时频图像。然后，提出一种简易二维卷积神经网络模型，将对应不同故障类型的时频图像输入该模型进行训练和测试。采用凯斯西储大学滚动轴承数据集进行实验，验证了所提方法的有效性，且诊断准确性优于其他几种常见的机器学习方法。

2. 相关理论及方法

2.1. 短时傅里叶变换

由于傅里叶变换只揭示了信号在频域的特点，却无法在时域中研究信号。因此，为了实现时域与频域之间的联动，本文采用短时傅里叶变换(STFT)来对信号进行时频域变换，以囊括更加丰富的特征信息。

实际上，短时傅里叶变换就是带有窗函数的傅里叶变换，尤其相比于后者更适合分析时变、非平稳信号。具体来说，在执行傅里叶变换之前，会将信号与一个时间有限的窗函数h(t)相乘。并且假设非平稳信号在分析窗的短时间间隔内是平稳的。通过在时间轴上移动窗函数h(t)，可以分段分析信号，从而获得信号的一系列局部“频谱”。短时傅里叶变换定义为：

$STFT\left(u,w\right)={\displaystyle {\int }_{-\infty }^{\infty }x\left(t\right)}h\left(t-u\right){\text{e}}^{-jwt}dt$ (1)

上式中，x(t)为待变换的信号。

2.2. 卷积神经网络

卷积神经网络(Convolutional Neural Network, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络。作为深度学习的代表算法之一，CNN因采用局部连接和权值共享而在计算机视觉等领域内大放异彩。因此，本文采用一种简易的卷积神经网络架构作为轴承故障分类的算法模型。

2.2.1. 卷积层

卷积层是卷积神经网络中的核心部分，主要负责对输入数据进行特征提取。卷积神经网络之所以能够自动提取故障特征，就是因为卷积层通过多个权值相等的卷积核进行滑动地卷积运算，以对输入信号进行局部特征提取。卷积层的卷积计算，公式如下：

$x_i^k=f\left({\omega }_i^k\ast x_i^{k-1}+b_i^k\right)$ (2)

上式中， $x_i^k$ 代表第k层输出的第i个特征， ${\omega }_i^k$ 表示第k层的第i个卷积核的权重，*为卷积运算符号， $x_i^{k-1}$ 为第(k − 1)层输出的第i个特征， $b_i^k$ 为偏置值；f为ReLU激活函数，相关介绍见2.2.3节。

2.2.2. 池化层

池化层，又称下采样层，通常和卷积层在卷积神经网络中交替出现。通过池化层对输入信息进行下采样，既能减少数据处理量，又可保留关键特征信息。池化层有平均池化层、最大池化层等，本文选用最大池化层，其公式如下：

$p_i^{l+1}\left(j\right)=\max x_i^j\left(k\right),k\in D_j$ (3)

上式中， $p_i^{l+1}$ 为最大池化层输出， $x_i^j$ 表示最大池化层输入。

2.2.3. 激活函数层

激活函数，又称“非线性映射函数”，在深度卷积神经网络模型中起到了不可或缺的作用，充当着至关重要的网络层角色。激活函数将输入数据进行非线性变换后再输出，使得神经网络具有了非线性属性，从而可以逼近非线性函数。常见的激活函数种类有Sigmoid函数、Tanh函数、ReLU函数等，本文选用ReLU函数，公式如下：

$f\left(x\right)=\max \left(0,x\right)$ (4)

2.2.4. 分类器

由于轴承故障诊断是典型的多分类任务，因此本文选用Softmax分类器。Softmax分类器使用Softmax函数，可将神经网络输出转化为概率分布，公式如下：

$S_i=\frac{e^{a_i}}{{\displaystyle \underset{j=1}{\overset{k}{\sum }}{e}^{a_j}}}$ (5)

上式中， $S_i$ 代表输出的第i类别概率值，a_i表示相连的全连接层输入到Softmax分类器中的第i个值。

3. 基于二维卷积神经网络轴承故障诊断方法流程

3.1. 网络架构

本文提出一种用于轴承故障诊断的简易卷积神经网络，由三个卷积层、三个最大池化层、四个ReLU激活函数层、三个批量归一化(Batch Normalization, BN)层、两个全连接层交替组成。另外在两个全连接层之间的ReLU激活函数层之后，采用dropout操作缓解过拟合，参数设置为0.2。本文所用的卷积神经网络架构及诊断流程图如图1所示；卷积神经网络具体架构参数如表1所示。

Figure 1. Fault diagnosis flowchart based on convolutional neural network

图1. 基于卷积神经网络的故障诊断流程图

Table 1. Convolutional neural network architecture parameters

表1. 卷积神经网络架构参数

3.2. 方法流程

•首先，根据轴承故障数据集，确定不同故障类别下对应的原始振动信号；

•其次，从不同类别的原始信号中选取信号段作为一维数据集，并划分为训练集和测试集；

•然后，根据数据集中不同类别样本，分别进行短时傅里叶变换，得到对应着不同故障类别的二维时频图像样本；

•再将二维时频图像训练集经过尺寸压缩、转为灰度图、标准化等预处理步骤之后，输入二维卷积神经网络架构进行训练；

•最后，将测试集中的二维时频图像样本输入训练好的模型中进行测试。

4. 实验设置与结果

4.1. 数据集描述

本文采用凯斯西储大学轴承数据集作为实验数据。实验数据采样频率为12,000 Hz，选用驱动端轴承数据，轴承型号为SKF6205，电动机负载0 HP，电动机转速1797 rpm。本文选用数据集的故障位置有滚动体、内圈、外圈，故障尺寸有0.007 inches、0.014 inches、0.021 inches，再包括健康轴承，一共10个故障类别，每种类别各有100个训练集样本和20个测试集样本。具体的故障类别与数据集划分详情如表2所示。

Table 2. Fault classes and dataset segmentation

表2. 故障类别与数据集划分

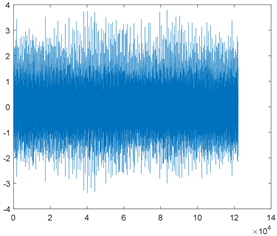
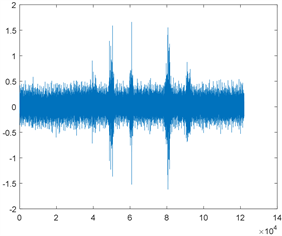
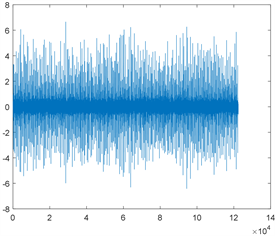
本文将一维时域振动信号进行短时傅里叶变换，输出二维时频图后作为二维卷积神经网络的输入。一维时域振动信号示意图如图2所示，经短时傅里叶变换后得到的二维时频图的示意图如图3所示。

4.2. 实验结果与分析

进行故障诊断实验，训练轮次epochs设置为20，采用交叉熵损失函数、Adam优化器，初始学习率设置为0.001。二维时频图预处理压缩为64 × 64尺寸。训练完成后进行测试得到测试准确率，连续重复五次取平均值。本文方法与其余四种对比方法的平均准确率如图4所示，本文所用2DCNN方法平均准确率最高，达到99.20%。1DCNN方法也取得了94.00%的平均准确率，但是仍低于本文2DCNN方法；MLP方法、SAE + SVM方法和BiLSTM方法的平均准确率均低于50.00%，明显劣于卷积神经网络方法。

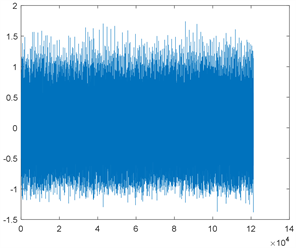
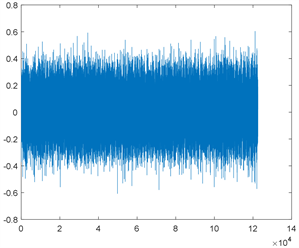
类别1 类别2

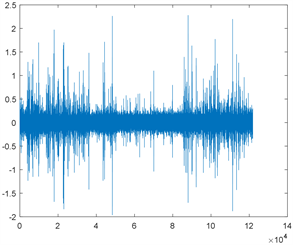
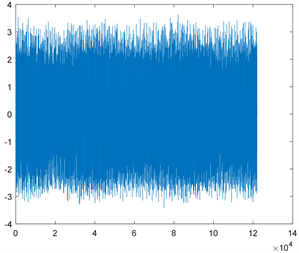
类别3 类别4

类别5 类别6

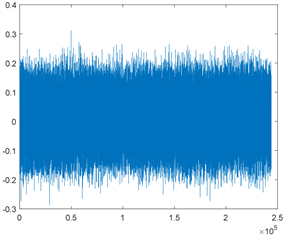
类别7 类别8类别9 类别10

Figure 2. One-dimensional time-domain vibration signal map

图2. 一维时域振动信号图

由于图4中明确显示出SAE+SVM方法和BiLSTM方法的平均准确率均不超过35%，说明这两种方法的诊断能力较差，因此不具备进一步分析的价值 [9] 。本文所用2DCNN方法，以及作为对比的1DCNN方法、MLP方法，训练准确率随epochs变化曲线如图5所示。不难看出，本文所用2DCNN方法的训练准确率曲线优于1DCNN方法和MLP方法，说明2DCNN的拟合速度快，学习故障特征信息的能力较强。而1DCNN能力稍弱于2DCNN，MLP则明显弱于以上两者。

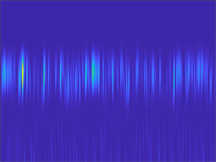
类别1 类别2

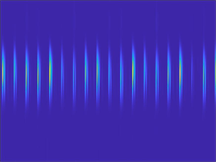
类别3 类别4

类别5 类别6

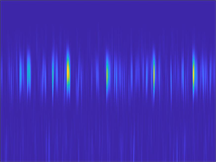类别7 类别8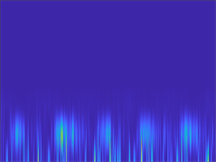类别9 类别10

Figure 3. Time-frequency diagrams after short-time Fourier transforms

图3. 短时傅里叶变换后的时频图

本文所用2DCNN方法，以及作为对比的1DCNN方法、MLP方法，训练损失值随epochs变化曲线如图6所示 [10] 。容易看出，本文2DCNN方法的损失值曲线无论是从稳定性上还是学习速度上来看，都优于1DCNN方法和MLP方法。虽然1DCNN方法的准确率好于MLP方法，但是前者损失值曲线具有明显的波动。

Figure 4. Average accuracy chart

图4.平均准确率图

Figure 5. Training accuracy graph

图5. 训练准确率图

进一步通过混淆矩阵图来分析本文所用2DCNN方法，以及作为对比的1DCNN方法、MLP方法，如图7所示 [11] 。不难看出，本文所用2DCNN方法的测试集准确率优于1DCNN方法、MLP方法，其中MLP方法的准确率较差，混淆矩阵图中近半数样本都没有被预测到正确的标签下。

可通过T-SNE可视化方法进一步观察三种方法中测试集样本在最后一个全连接层的分布情况 [12] 。T-SNE可视化图如图8所示。T-SNE可视化图能够清晰直观地展示出网络模型对于测试样本分类的情况，图8中本文2DCNN方法的分布类内更加聚集，类间距离清晰可分。1DCNN方法的分布稍逊于2DCNN方法，但是MLP方法的分布则非常杂乱无章、难以区分。

Figure 6. Training loss value graph

图6. 训练损失值图

Figure 7. Confusion matrix graph

图7. 混淆矩阵图

Figure 8. T-SNE visualization map

图8. T-SNE可视化图

5. 结论

本文提出了一种轴承故障智能诊断方法，首先确定不同故障类别下对应的原始振动信号，选取信号段制作一维信号数据集，再进行短时傅里叶变换转化为时频图，紧接着输入本文提出的二维卷积神经网络架构训练、测试，能够在结构并不复杂的前提下实现轴承故障“端到端”的智能诊断。为了验证本文方法的有效性，采用凯斯西储大学轴承数据集进行实验。实验结果表明，本文所用2DCNN方法的平均准确率达到99.20%，明显优于其余四种用于对比的机器学习方法。并且经过分析训练准确率、训练损失值、混淆矩阵图和T-SNE可视化图，进一步验证了本文所用2DCNN方法的有效性和相比于其他方法的优势。