高校理工类课程思政成绩多维度模糊综合评价——以《概率论与数理统计》课程为例

Multidimensional Fuzzy Comprehensive Evaluation of the Score of Ideological and Political in Higher Education Science and Engineering Courses—Taking the Course of “Probability Theory and Mathematical Statistics” as an Example

摘要: 为了更加客观、公正评价高校理工类学生课程思政成绩，本文以《概率论与数理统计》课程为例，通过主成分分析法和层次分析法构建了课程思政多层次评价指标体系，从授课教师、组间同学和学生自身三个维度，运用模糊综合评判构建了课程思政成绩多维度模糊综合评价模型，并将指标体系和综合评价模型应用于我校通信工程专业的《概率论与数理统计》课程思政成绩评测。实例结果表明，所构建的指标体系和评价模型能够得到较客观的课程思政成绩，具有较强的操作性。

Abstract: To objectively and fairly evaluate the course ideological and political grades for science and engineering students in university, this paper takes the course “Probability Theory and Mathematical Statistics” as an example and constructs a multi-level evaluation index system for ideological and political education in courses by the principal component analysis and analytic hierarchy process. From the perspectives of teachers, inter-group students, and students themselves, the paper proposes a multi-dimensional fuzzy comprehensive evaluation model for ideological and political education in courses by the fuzzy comprehensive evaluation. The index system and comprehensive evaluation model are applied to the evaluation of ideological and political achievements in the course “Probability Theory and Mathematical Statistics” in the Communication Engineering major of our university. The example results show that the constructed indicator system and evaluation model can obtain more objective course ideological and political grades, and have strong operability.

1. 引言

课程思政评价是高校课程思政教学质量持续改进的重要手段。教育部在2020年印发的《高等学校课程思政建设指导纲要》指出，要结合不同课程特点分类推进高校课程思政建设。理工类课程具有抽象性高、逻辑性强以及应用性广等特点。因此，如何结合课程特点对高校理工类课程思政效果进行客观准确评价，是推动理工类专业课程思政教学质量持续改进，促进学生综合素质提升的核心问题。

现有文献多是从宏观层面对课程思政评价进行研究，例如，苏小菱等 [1] 以层次分析法为支撑构建了课程思政的育人质量评价模型，许祥云等 [2] 基于CIPP评价模型构建了高校课程思政综合评价指标体系，陈世月等 [3] 结合德尔菲法和层次分析法构建了高校课程思政教学评价指标体系，魏继宗等 [4] 结合德尔菲法和层次分析法构建了高校课程思政教学评价指标体系，郭芳 [5] 结合层次分析法和熵权法提出了课程思政评价模型。近期，也有针对理工类课程从微观层面开展课程思政评价相关工作，例如，乔维德等 [6] 基于CIPP-AHP和BP神经网络建立了高职院校专业课程思政教学评价模型，吴晓艳等 [7] 以工程热力学课程为例开展了思政教学效果评价，马慧颖等 [8] 以Python程序设计语言为例对课程思政教学评价进行了定性探究，周霖 [9] 通过模糊层次分析法构建了高等数学课程的思政教学评价指标体系。

以上研究对理工类课程思政教学质量的提高具有一定的促进作用，但大都是从授课教师角度对课程思政进行评价，缺乏从学生成绩角度的评价研究。由于课程思政成绩评价涉及的因素较多，评价指标受考评者知识水平、认知能力和个人偏好的直接影响，而且，评价指标一般都是定性描述，有鲜明的模糊特征，给具体操作带来一定的困难。此外，评价工作需从不同的层次、不同的维度进行，客观上要求分层次进行综合评价，因而课程思政成绩评价是一个多层次、多维度的模糊综合评价问题。针对以上问题，本文拟结合模糊综合评判、层次分析法和主成分分析法，以《概率论与数理统计》课程为例，联系我校教学实践，开展理工类课程思政成绩评价实践，为课程思政的教学改革和创新提供参考。

2. 课程思政成绩多层次评价指标体系

2.1. 评价指标集的确定

根据《高等学校课程思政建设指导纲要》中理工科课程思政建设的目标要求、近三年用人单位对我校理工类专业应届毕业生的反馈以及数学学科核心素养 [10] ，结合《概率论与数理统计》课程的特点，《概率论与数理统计》课程思政成绩评价主要包括科学思维、科学精神和责任担当三个方面，其中，科学思维包括信息意识、随机思维、逻辑思维、逆向思维、辩证思维等；科学精神包括批判质疑、探索实践、求真务实、开拓创新等；责任担当包括文化自信、团队协作、诚信友善、传统文化等。运用主成分分析法 [11] 将评价指标约简为11项指标，通过层次分析法 [12] ，将《概率论与数理统计》课程思政成绩评价指标分解为三个层次，评价指标体系如图1所示。

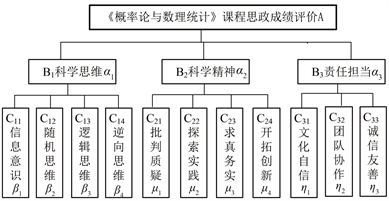
Figure 1. A multi-level evaluation index system for ideological and political achievements in the course of “Probability Theory and Mathematical Statistics”

图1. 《概率论与数理统计》课程思政成绩多层次评价指标体系

图1中，I = A为第一层指标集， $\text{A}=\left({\text{B}}_{\text{1}},{\text{B}}_{\text{1}},{\text{B}}_{\text{3}}\right)$ 为第二层指标集， ${\text{B}}_{\text{1}}=\left({\text{C}}_{\text{11}},{\text{C}}_{\text{12}},{\text{C}}_{\text{13}},{\text{C}}_{\text{14}}\right)$ ， ${\text{B}}_{\text{2}}=\left({\text{C}}_{\text{21}},{\text{C}}_{\text{22}},{\text{C}}_{\text{23}},{\text{C}}_{\text{24}}\right)$ ， ${\text{B}}_{\text{3}}=\left({\text{C}}_{\text{31}},{\text{C}}_{\text{32}},{\text{C}}_{\text{33}}\right)$ 为第三层指标集。 ${\alpha }_i\left(i=1,2,3\right)$ 为二级指标B_i的权重， ${\beta }_i\left(i=1,2,3,4\right)$ 为三级指标C_1i的权重， ${\mu }_i\left(i=1,2,3,4\right)$ 为三级指标C_2i的权重， ${\eta }_i\left(i=1,2,3\right)$ 为三级指标C_3i的权重。

2.2. 评价指标权重的确定

通过和积法确定图1中的指标权重，具体步骤为：首先，将各层次不同指标进行两两比较，由专家按照Saaty的1~9标度法 [12] 对同一层次内不同指标的相对重要性进行打分；其次，根据专家打分结果，构造各层次指标重要度的判断矩阵；最后，分别计算各层次判断矩阵的特征向量，其分量即为各层次评价指标的权重。表1列出了《概率论与数理统计》课程思政成绩评价体系中各级指标的权重。

3. 课程思政成绩多维度模糊综合评价模型

为了尽可能全面、客观、合理地反映学生的课程思政成绩，从不同评价者有利于作出客观评价的角度出发，对学生课程思政成绩的测评采用授课教师评价，组间同学评价和学生自身评价相结合的形式。

Table 1. Weights of evaluation indicators for ideological and political achievements in the course of “Probability Theory and Mathematical Statistics”

表1. 《概率论与数理统计》课程思政成绩评价指标权重

3.1. 隶属度矩阵的构造

设学生《概率论与数理统计》课程思政成绩评价分优秀，良好，中等，差和较差五个等级。令 $V=\left(V_1,V_2,V_3,V_4,V_5\right)$ = (优秀，良好，中等，差，较差)为课程思政评价集，各层次指标的隶属度矩阵为

$R={\left(r_{ij}\right)}_{m\times 5}=\left[\begin{array}{ccccc}{r}_{11}& r_{12}& r_{13}& r_{14}& r_{15}\\ r_{21}& r_{22}& r_{23}& r_{24}& r_{25}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ r_{m1}& r_{m2}& r_{m3}& r_{m4}& r_{m5}\end{array}\right],$

其中， $r_{ij}=\left(r_{i1},r_{i2},r_{i3},r_{i4},r_{i5}\right)\left(i=1,2,\cdots ,m\right)$ 为隶属度，即第i个指标在第j个评价等级上的频率分布，需要满足 ${\displaystyle \underset{j=1}{\overset{5}{\sum }}{r}_{ij}}=1$ ，如不满足，需做归一化处理。

3.2. 多层次模糊综合评价

根据图1的层次结构，分别对授课教师评价、组间同学评价和学生自身评价由最末层开始分配权重并计算相应的隶属度矩阵，直到第一层。

1. 第三层指标的模糊综合评价

${\tilde{R}}_{C_1}={\left[\begin{array}{cccc}{R}_{C_{11}}& R_{C_{12}}& R_{C_{13}}& R_{C_{14}}\end{array}\right]}^{\text{T}}$ ， ${\tilde{R}}_{C_2}={\left[\begin{array}{cccc}{R}_{C_{21}}& R_{C_{22}}& R_{C_{23}}& R_{C_{24}}\end{array}\right]}^{\text{T}}$ ， ${\tilde{R}}_{C_3}={\left[\begin{array}{ccc}{R}_{C_{31}}& R_{C_{32}}& R_{C_{32}}\end{array}\right]}^{\text{T}}$ .

2. 第二层指标的模糊综合评价

${\tilde{R}}_{B_1}=M_{B_1}{\tilde{R}}_{C_1}$ ， ${\tilde{R}}_{B_2}=M_{B_2}{\tilde{R}}_{C_2}$ ， ${\tilde{R}}_{B_3}=M_{B_3}{\tilde{R}}_{C_3}$ .

归一化处理得第二层总评价矩阵 ${\tilde{R}}_B={\left[\begin{array}{ccc}{R}_{B_1}& R_{B_2}& R_{B_3}\end{array}\right]}^{\text{T}}$ 。

3. 第一层指标的模糊综合评价

${\tilde{R}}_A=M_A{\tilde{R}}_B.$

4. 授课教师、组间同学和学生自身的模糊综合评价

利用和积法确定授课教师、组间同学和学生自身的权重集为 ${\rm M}=\left({\alpha }_1,{\alpha }_2,{\alpha }_3\right)$ ，授课教师、组间同学和学生自身对学生课程思政成绩的综合评价向量为 $\tilde{R}=M{\left[{\tilde{R}}_A,{{\tilde{R}}^{\prime }}_A,{{\tilde{R}}^{″}}_A\right]}^{\text{T}}$ ，其中 ${{\tilde{R}}^{\prime }}_A$ ， ${{\tilde{R}}^{″}}_A$ 分别表示组间同学和学生自身对第一层次指标的评价向量。

5. 综合评价结果的定量表示

为了将评价结果定量化，对评价等级 $V_j\left(j=1,2,3,4,5\right)$ 进行赋值，用矩阵表示为

$G={\left[\begin{array}{ccccc}{G}_1& G_2& G_3& G_4& G_5\end{array}\right]}^{\text{T}}.$

某学生《概率论与数理统计》课程思政成绩的综合评价结果可定量表示为

$X=\tilde{R}{\left[\begin{array}{ccccc}{G}_1& G_2& G_3& G_4& G_5\end{array}\right]}^{\text{T}}.$

4. 评价实例

4.1. 数据收集

根据本文构建的多层次评价指标体系，我们设计了包含① 信息意识，② 随机思维，③ 逻辑思维，④ 逆向思维，⑤ 批判质疑，⑥ 探索实践，⑦ 求真务实，⑧ 开拓创新，⑨ 文化自信，⑩ 团队协作，⑪ 诚信友善11个评价指标的《概率论与数理统计》课程思政成绩综合评价调查问卷，并向西安邮电大学2022级通信工程专业106名学生及《概率论与数理统计》课程的2名授课教师发放了问卷调查，让学生本人、组间同学、授课教师分别对评价对象的课程思政情况，从优秀、良好、中等、差、较差这五项评价中做出相应选择，以收集该专业学生《概率论与数理统计》课程思政的教师评价、同学评价及自我评价结果，最终收回2份授课教师及105份学生的有效问卷。

4.2. 模糊综合评价

以西安邮电大学通信工程2201班的周**同学为例，利用本文提出的多维度模糊综合评价模型对该同学《概率论与数理统计》的课程思政成绩进行综合评价。根据收集的有关周**同学《概率论与数理统计》课程思政评价的调查问卷，通过模糊数学知识逐层计算授课教师、组间同学和学生本人对周**同学《概率论与数理统计》课程思政成绩各指标的评价结果。

1. 授课教师对第三层指标的综合评价

授课教师对周**同学《概率论与数理统计》课程思政科学思维、科学精神、责任担当的评价矩阵分别为

${\tilde{R}}_1=\left[\begin{array}{ccccc}0.5& \text{0}\text{.26}& \text{0}\text{.2}& \text{0}\text{.03}& \text{0}\text{.01}\\ \text{0}\text{.48}& \text{0}\text{.32}& \text{0}\text{.18}& \text{0}\text{.02}& \text{0}\\ \text{0}\text{.1}& \text{0}\text{.36}& \text{0}\text{.3}& \text{0}\text{.2}& \text{0}\text{.04}\\ \text{0}\text{.2}& \text{0}\text{.38}& \text{0}\text{.28}& \text{0}\text{.1}& \text{0}\text{.04}\end{array}\right],$

${\tilde{R}}_2=\left[\begin{array}{ccccc}0.24& \text{0}\text{.48}& \text{0}\text{.2}& \text{0}\text{.06}& \text{0}\text{.02}\\ \text{0}\text{.28}& \text{0}\text{.44}& \text{0}\text{.2}& \text{0}\text{.07}& \text{0}\text{.01}\\ \text{0}\text{.02}& \text{0}\text{.28}& \text{0}\text{.42}& \text{0}\text{.2}& \text{0}\text{.02}\\ \text{0}\text{.12}& \text{0}\text{.4}& \text{0}\text{.25}& \text{0}\text{.18}& \text{0}\text{.05}\end{array}\right],$

${\tilde{R}}_3=\left[\begin{array}{ccccc}0.46& 0.28& 0.22& 0.03& 0.01\\ 0.36& 0.4& 0.18& 0.04& 0.02\\ 0.3& 0.52& 0.15& 0.02& 0.01\end{array}\right].$

2. 授课教师对第二层指标的综合评价

授课教师对周**同学科学思维的评价向量为

$\begin{array}{c}{\tilde{R}}_{B1}=\left(0.\text{2},0.\text{2},0.\text{2},\text{0}\text{.4}\right)\left[\begin{array}{ccccc}0.5& \text{0}\text{.26}& \text{0}\text{.2}& \text{0}\text{.03}& \text{0}\text{.01}\\ \text{0}\text{.48}& \text{0}\text{.32}& \text{0}\text{.18}& \text{0}\text{.02}& \text{0}\\ \text{0}\text{.1}& \text{0}\text{.36}& \text{0}\text{.3}& \text{0}\text{.2}& \text{0}\text{.04}\\ \text{0}\text{.2}& \text{0}\text{.38}& \text{0}\text{.28}& \text{0}\text{.1}& \text{0}\text{.04}\end{array}\right]\\ =\left(\text{0}\text{.296},\text{0}\text{.34},\text{0}\text{.248},\text{0}\text{.09},\text{0}\text{.026}\right).\end{array}$

同理可得授课教师对周**同学科学精神、责任担当的评价向量分别为

$R_{B_2}=\left(0.1\text{46},0.3\text{88},0.2\text{81},0.1\text{4},0.0\text{27}\right)$ ， $R_{B_3}=\left(0.3\text{72},0.\text{400},0.1\text{83},0.03\text{1},0.014\right)$ ，

从而得第二层主因素的评价矩阵为

${\tilde{R}}_B=\left[\begin{array}{ccccc}\text{0}\text{.296}& \text{0}\text{.34}& \text{0}\text{.248}& \text{0}\text{.09}& \text{0}\text{.026}\\ 0.1\text{46}& 0.3\text{88}& 0.2\text{81}& 0.1\text{4}& 0.0\text{27}\\ 0.3\text{72}& 0.\text{400}& 0.1\text{83}& 0.03\text{1}& 0.014\end{array}\right].$

3. 授课教师对第一层指标的综合评价

利用和积法确定出授课教师、组间同学和自身评价的权重集为 $M=\left(0.4,0.3,0.3\right)$ ，从而授课教师对第一层指标的评价向量为

$\begin{array}{c}{\tilde{R}}_A=\left(0.\text{4},0.\text{4},0.3\right)\left[\begin{array}{ccccc}\text{0}\text{.296}& \text{0}\text{.34}& \text{0}\text{.248}& \text{0}\text{.09}& \text{0}\text{.026}\\ 0.1\text{46}& 0.3\text{88}& 0.2\text{81}& 0.1\text{4}& 0.0\text{27}\\ 0.3\text{72}& 0.\text{400}& 0.1\text{83}& 0.03\text{1}& 0.014\end{array}\right]\\ =\left(0.2\text{884},0.\text{4112},0.2\text{665},0.\text{1013},0.02\text{54}\right).\end{array}$

4. 授课教师、组间同学和学生自身对课程思政的综合评价

用同样的方法可得到组间同学和学生自身对课程思政的评价向量分别为

${{\tilde{R}}^{\prime }}_A=\left(0.264,0.314,0.33,0.092,0\right)$ ， ${{\tilde{R}}^{″}}_A=\left(0.44,0.405,0.155,0,0\right)$ .

则周**同学《概率论与数理统计》课程思政的综合评价向量为

$\begin{array}{c}\tilde{R}=M{\left[{\tilde{R}}_A,{{\tilde{R}}^{\prime }}_A,{{\tilde{R}}^{″}}_A\right]}^{\text{T}}\\ =\left(0.326\text{6},0.3\text{802},0.2\text{521},0.06\text{81},0.0\text{102}\right).\end{array}$

5. 综合评价结果的定量表示

上述结果表明参评的人员中约32.66%的人认为该学生的思政评价“优秀”，38.02%人认为该学生的思政评价“良好”，25.21%的人认为该学生的思政评价“中等”，6.81%的人认为该学生的思政评价“差”，1.02%的人认为该学生的思政评价“较差”。若使这一结果能以百分制的形式表示出来，可规定100分为“优秀”，85分为“良好”，75分为“中等”，60分为“差”，40分为“较差”，则可得赋值向量

$G=\left(100,85,75,60,40\right),$

从而，周**同学在《概率论与数理统计》中的思政评价综合得分为

$X=\left(0.326\text{6},0.3\text{802},0.2\text{521},0.06\text{81},0.0\text{102}\right)\left(\begin{array}{c}100\\ 85\\ 75\\ 60\\ 40\end{array}\right)=8\text{8}\text{.3785}\text{.}$

根据周**同学的平时表现情况，这一结果比较准确地反映了该学生实际的思政素养。

5. 结论

本文根据理工类课程思政成绩评价中存在的多层次、多维度和模糊性等特点，从《高等学校课程思政建设指导纲要》、数学学科核心素养以及用人单位反馈三方面，以学生《概率论与数理统计》课程思政成绩评价为例，通过主成分分析法和层次分析法构建了课程思政成绩多层次评价指标体系，从授课教师、组间同学、学生自身三个维度，通过模糊综合评判构建了课程思政成绩多维度模糊综合评价模型。通过对西安邮电大学通信工程专业学生的《概率论与数理统计》课程思政成绩的实例评价得到，结合主成分分析法、层次分析法和模糊综合评判的课程思政成绩评价方法能够把影响学生课程思政成绩的多种模糊因素进行综合定量考虑，避免了个人主观臆断的不足，较好地保证了课程思政成绩的客观、公平和操作实用性。

基金项目

陕西省教师教育改革与教师发展研究项目(2023053)，陕西省教育教学改革研究项目(23BY096)，高等学校大学数学教学研究与发展中心项目(CMC20220104)，《概率论与数理统计》国家一流课程、省级课程思政示范课程，《概率论与随机过程》校级课程思政示范课程。