1. 引言
解三角形是高中数学学习的重点内容之一,它涉及正弦定理、余弦定理、三角形面积公式及三角函数,基本不等式等知识的综合应用,同时还蕴含很多数学思想方法,通过解三角形专题内容的学习,有助于学生数学运算,逻辑推理等核心素养水平的进一步提升,三角形最值问题是解三角形中常见的考点之一,考查的方式灵活多变,需要学生具备较强的综合能力,归纳总结解决此类问题的规律和技巧,有利于帮助学生发散思维、掌握解决问题的思路方法,提高解题效率。为此很多学者和一线的教师对其进行了深入的研究。对于解三角形高考命题导向,郝文华对近九年(2012~2020)高考数学全国卷中的解三角形试题进行分析探究,了解命题特点,提出了备考建议 [1] 。薛红霞,张士彩基于2022年高考数学试卷中的三角函数与解三角形试题,分析了试题特点和命题导向,并在此基础上提出了相应的教学建议 [2] 。石秀成、李多敏从一道高考题引发了关于解三角形的思考,通过深入分析探究,提出了备考建议 [3] 。关于解题方面,范习昱通过精选了部分高考题,加以分类例析,总结出了解三角形常考的题型及解题规律 [4] 。刘光明基于新课标的要求和新教材的导向,结合高三复习教学实践,提出解三角形问题一般可以从定理、几何、解析、基底和转化五个方面进行探索 [5] 。盛耀建,车承梅等人提出可以从几何图形入手,将代数问题转化为几何问题,借助于平面几何的知识,解决解三角形问题 [6] [7] 。韩涛、商波波则提出可以通过借助于坐标运算的方法,将解三角形转化到解析几何中,使求解更直接、更具有操作性 [8] 。丁玉霞针对解三角形的最值问题,提出可以利用二次函数的性质,基本不等式法,三角函数的性质,圆的性质来求解问题 [9] 。丁崇芳,潘敬贞以2022年全国甲卷理数第16题和2022年新高考全国I卷第18题为例,从不同视角,对问题进行分析变形,探索如何通过恰当的选择变量,优化解题过程,提高解题效率 [10] 。本文主要从几何和代数两个不同角度,探究三角形周长与面积最值问题的解题规律和方法。
2. 周长最值模型
已知三角形一边的长度及其所对角,求周长最值,通常可以从代数和几何两个角度来解决问题。代数角度主要有以下两个思路:(1) 边化角,然后根据正弦定理结合三角函数求解;(2) 角化边,根据余弦定理结合基本不等式进行求解。
例1. (2020年全国二卷)
中,
(1) 求A
(2) 若
,求
周长的最大值。
解:(1)
(求解过程省略)
(2) 解法一:已知
,根据正弦定理可得:
,
,
,故
,又因为
,故当
时,
周长取得最大值为
。
解法二:根据正弦定理
,化简得
,即
,又根据基本不等式得:
,即
,
,故
周长的最大值为
。
解法三:延长BA至点D,使得
连接CD,如图1所示。
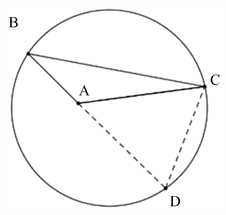
Figure 1. Example 1 Geometric method analysis schematic
图1. 例题1几何法分析示意图
已知
,故
,又因为
,故
,在
中根据正弦定理可得,
,点D是直径为
的圆上弦BC所对优弧上的动点,由圆的性质知当弦BD过圆心的时候,取得最大值为
,故
周长的最大值为
。
评注:本题代数方面,将角化边结合基本不等式来求解,过程相对容易一些,如果将边化角,求解过程中涉及诱导公式等相关知识,计算相对繁杂,但在日常教学中可以让学生动手实践,感受不同方法解题的过程,拓展解题思路,选择最优的解题方案。
3. 面积最值模型
(1) 已知三角形的一条边长及其对角求面积最值的方法和求周长最值一样,可以从代数和几何两个角度解决,代数角度主要有以下两个思路:① 边化角,然后根据正弦定理结合三角函数求解;② 角化边,根据余弦定理结合基本不等式进行求解。
例2、(2014年新课标Ⅰ)已知
分别为
的三个内角
的对边,
且
,则
面积的最大值为_____。
解法一:根据正弦定理,
可得,
,又已知
,故
,
,又已知
,根据基本不等式得
,
,
面积的最大值为
。
解法二:
,故
,
,
,
,
,当
时,
的面积取得最大值为:
。
解法三:由正弦定理得
(2R为三角形外接圆直径)点A是直径为
的圆上弦BC所对优弧上的动点,由圆的性质可知,当边BC边上的高经过圆心时,如图2所示。
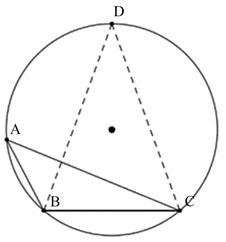
Figure 2. Example 2 Geometric method analysis schematic
图2. 例题2几何法分析示意图
最大,此时
,
,
。
评注:本题几何角度根据三角形的面积公式,容易联想到数形结合,结合圆的性质进行求解。
(2) 已知三角形的一个角及其邻边
例3 (2019新课标II)
的内角
的对边分别为
,已知
(1) 求B
(2) 若
为锐角三角形,且
,求
面积的取值范围
解:(1)
(求解过程省略)
(2) 由题设及(1)知
的面积
,根据正弦定理可得,
,由于
为锐角三角形,故
,
,又因为
,故
,所以
,
,即
。
评注:本题已知三角形的一角及其邻边,主要是通过正弦定理及三角函数的相关知识,计算三角形面积的取值范围。