1. 引言
随着信息化和智能化时代的到来,离散时间排队系统的应用日益广泛。在计算机系统中,信息存储的单位是字节;在宽带综合业务数字网络中,信号传输都是将网络信号分割成等长的信元进行传送。这些领域处理的数据都是正整数值随机变量,适合用离散时间排队系统进行处理。因此对离散时间随机服务进行研究具有很好的应用价值。自Meisling [1] 开创了离散时间排队系统的研究之后,连续时间排队系统中大量的研究结果也被推广到了离散时间排队系统当中。学者们也不再局限于简单的Geo/Geo/1系统,而是在此基础上考虑了更为复杂的情形,如顾客成批到达、服务时间服从PH分布、启动期和工作休假策略等 [2] [3] [4] [5] [6] 。为了使离散时间排队系统更具有应用价值,Atencia和Moreno [7] 首次将负顾客策略引入到Geo/Geo/1排队系统。后来的学者们则在带负顾客的离散时间排队系统中进一步考虑了N策略、休假策略以及工作故障等情况 [8] [9] [10] [11] 。这些策略使得离散时间排队系统更加贴合实际情况,关于离散时间排队系统的研究也愈发成熟。
基于博弈论的排队经济学理论是一个快速发展的研究领域。近些年来,对带负顾客的排队系统进行经济分析已经成为一个热门主题 [12] 。排队系统中的顾客和服务商都拥有着自主决策权,他们的自主行为将直接影响到系统的性能,使得排队策略具有灵活性,也更加符合实际情况 [13] 。因此,对排队系统中的优化设计和优化控制问题进行经济学分析,对顾客和管理者而言,都具有很强的现实指导意义。在Naor [14] 首次对排队系统进行经济分析并给出了纳什均衡策略之后,关于带负顾客的连续时间排队系统的均衡策略研究目前已经十分完善。Wang等 [15] [16] 在带有负顾客的连续时间排队系统中先后考虑了故障可修和N策略的情形,并对系统进行了经济分析,探究了可视状态和不可视状态下的纳什均衡策略。Panda和Goswami [17] 从经济学的角度出发,将带有负顾客的连续时间排队系统与工作休假情形相结合,给出了不同信息水平下顾客的均衡策略。然而,考虑到模型的复杂性和难度,目前还很少有人研究带负顾客的离散时间排队系统中顾客与企业的策略行为。傅裕蓉等 [18] 将具有破坏性的负顾客引入到Geo/Geo/1/MWV排队系统当中,证明了顾客存在唯一的均衡策略,但并未给出具体的解析解。基于上述研究,本文的主要创新点是将带负顾客的排队策略研究推广到离散时间排队系统当中,并在此基础上引入两种价格机制,进而研究顾客的均衡策略与企业的最优服务定价决策。
2. 模型描述
离散时间排队系统把时间轴分成若干个等长的部分,每个部分被称为一个时隙 [19] 。顾客的到达和离去只发生在时隙分点处,且顾客的到达间隔和服务时间都是正整数值的随机变量。本文考虑的是一个具有延迟入口的Geo/Geo/1晚到系统,如图1所示。
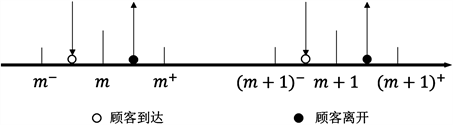
Figure 1. Diagram of the Geo/Geo/1 late arrival system with delayed entry
图1. 具有延迟入口的Geo/Geo/1晚到系统图
系统中存在两类顾客,正顾客和负顾客。正、负顾客均以Bernoulli过程到达系统:每一个时隙末端
上分别以概率
、
发生一个正到达和负到达,
。当正顾客到达并进入系统后,若系统处于空闲状态,则立刻接受服务,否则排队等候。负顾客进入系统后不接受服务,只会抵消正在接受服务的正顾客,不会对服务台造成损坏。若系统处于空闲状态,则到达的负顾客会自动消失。当正顾客和负顾客在同一时隙末端到达系统时,假定正顾客比负顾客先进入系统。
服务台在时隙首端
上开始服务,正顾客的服务时间服从参数为
的几何分布。系统按照先到先服务的原则提供服务,并且每次只能服务一名正顾客。假设每位正顾客的服务时间至少为一个单位时间,即当正顾客若在
到达系统,则该名顾客服务完成后离开至少发生在
上。假设系统中正、负顾客的到达过程和服务过程都是相互独立的。
令
表示
时刻系统中正顾客的数量。显然
是一个离散时间的马尔可夫过程,其状态空间
。令系统中的一步转移概率与平稳概率分别表示如下:
,
.
3. 可见情形
正顾客在到达系统时,能够知道系统中正顾客的数量n,并以此来决定是否进入队伍。假设每位正顾客在服务完成之后能够获得回报R,并且他们在系统中逗留期间的单位等待费用为C。此外,假设所有的正顾客都是完全理性且风险中立的,一旦做出决定后不能反悔,即选择进入系统后不能中途退出;选择止步后不能再返回。当系统处于空闲状态时,正顾客会选择进入排队系统接受服务。企业采用两种服务定价,一种是服务费用固定的收费机制,令
表示其费用;另一种则是与时间相关的收费机制,顾客需缴纳的服务费用是不固定的,且与逗留时间成正比,令
表示单位时间内的服务费用。
表示正顾客在这两种价格机制下的均衡策略,
表示企业在这两种价格机制下的最优服务定价决策。
基于上述描述,该模型属于一种动态博弈模型,称为斯塔克博格(Stackelberg)模型。顾客与企业之间博弈的顺序为:企业先进行服务定价,顾客在知道服务价格后根据自身的收益情况来决定是否进入队伍。在纳什均衡条件下,本文通过逆推归纳法研究顾客的策略行为,并在此基础上求出了企业的最优服务定价方案。
3.1. 顾客的平均逗留时间
假设标记顾客到达系统时发现队长为n,设
表示该标记顾客在系统中的平均逗留时间。标记顾客进入系统后,系统状态首次发生变化仅有两种情况才会对标记顾客产生影响,即服务结束首先发生或者负顾客到达首先发生。用
与
分别表示这两种情况发生的概率:
, (1)
, (2)
本文中任意
,记
,且易证
。
因此,标记顾客的平均逗留时间由两部分组成:(1)系统状态首次发生变化的平均时间;(2)系统状态首次发生变化后标记顾客的剩余平均逗留时间。前者用w来表示,因此,有:
。 (3)
故当标记顾客进入系统后,其平均逗留时间为:
, (4)
, (5)
解得:
, (6)
显然
关于n是严格单调递增的。
3.2. 顾客的均衡策略
本节将探讨在可见情形下,正顾客在两种价格机制下的均衡策略。当服务费用固定时,标记顾客进入系统后的期望净收益记为
;当服务费用不固定时,标记顾客的期望净收益记为
,则有:
,(7)
。 (8)
当
时,解得:
,
而当
时,解得:
。
分别令:
,
,
其中
表示不超过x的最大整数。因此,当服务费用固定时,标记顾客到达系统后,若队长
,则选择进入系统,否则选择止步。当服务费用不固定时,标记顾客到达系统后,若队长
,则选择进入系统,否则选择止步。
故在可见情形下的带负顾客的Geo/Geo/1排队系统中,顾客的均衡策略
为:
。
3.3. 企业收益分析
下面将探讨在可见情形下,企业在两种价格机制下的最优服务定价决策。当服务费用固定时,企业的均衡收益用
表示;当服务费用不固定时,企业的均衡收益用
表示,则有:
, (9)
。 (10)
注意:
,
,
故
是关于
的凹函数,存在最大值。当
时,
是关于
的凹函数,也存在最大值。因此,分别令:
,
,
求得:
,
。
因此,当定价分别为
与
时,企业收益可以达到最大值。故在可见情形下的带负顾客的Geo/Geo/1排队系统中,企业的最优服务定价决策
为:
。
4. 不可见情形
在不可见情形下,正顾客到达系统时,不知道系统中正顾客的数量n,但必须抉择是否进队。假设正顾客选择进队的概率为q,因此,正顾客的有效到达率为
。下面先对系统的状态进行分析。
4.1. 系统稳态分析
在不可见情形下,带负顾客的Geo/Geo/1排队系统的状态转移图如图2:

Figure 2. State transition diagram of Geo/Geo/1 queuing system with negative customers
图2. 带负顾客的Geo/Geo/1排队系统的状态转移图
因此,有以下一步转移概率:
,
,
,
,
,
,
,
。
得到一步转移概率后,根据Kolmogorov方程有:
即:
, (11)
, (12)
。 (13)
在不可见情形下,求系统的稳态指标需要从平稳概率出发,再根据平稳概率得到系统的平均队长以及平均逗留时间等各项指标。下面通过两个引理分别求出系统的平稳概率、平均队长和顾客的平均逗留时间。
引理1 在带负顾客的Geo/Geo/1排队系统中,当正顾客的有效到达率为
时,系统的稳态分布
可表示为:
证明:定义母函数 [7]
。公式(13)两边同乘
并对
进行求和,得到:
,
即:
(14)
结合公式(11)和公式(12),公式(14)可以改写为:
,
将上式进行化简,有:
,
于是,得到:
, (15)
进而有:
。
因为
,从而解得:
, (16)
, (17)
再由公式(11)可得:
。(18)
易证:
, (19)
, (20)
根据公式(20)容易验证:
,
与公式(18)结果一致。
引理2 在带负顾客的Geo/Geo/1排队系统中,当系统处于稳态时,顾客的平均逗留时间记为
,其表达式如下:
。
证明:系统队长的概率母函数为:
, (21)
因此,可以得出系统的平均队长
的表达式:
, (22)
再由Little公式 [20] ,可进一步得到顾客的平均逗留时间
的表达式:
。 (23)
由公式(22)与公式(23)可知,当
时,此时系统将变成无负顾客到达的离散时间Geo/Geo/1排队系统,其对应的系统稳态指标如下:
,
,
上述结果与文献 [19] 一致,说明本文所研究的带负顾客的Geo/Geo/1排队系统是文献 [19] 的一种推广形式。
4.2. 服务费用固定
这一节将探讨在服务费用固定的情况下,顾客的均衡策略和企业的最优服务定价问题。在不可见情形下带负顾客的Geo/Geo/1排队系统中,正顾客进入系统后,服务费用固定,用
表示。
表示在服务费用固定的情况下,正顾客选择进入队伍的均衡概率,因此,均衡到达率
。标记顾客进入系统后的期望净收益用
表示,企业单位时间内的期望收益用
表示,则有:
, (24)
, (25)
其中
表示在服务费用固定的情况下,正顾客在系统中所需的平均逗留时间,且
是有效到达率
的函数。
定理1在不可见情形下的带负顾客的Geo/Geo/1排队系统中,当服务费用固定时,顾客的均衡策略
为:
其中
,
。
证明:由公式(24)可知:
情况(1):当
时,即
时,此时正顾客的有效到达率为0,即当其余所有正顾客都不进入系统的情况下,标记顾客选择进入系统后的收益
。故均衡策略为止步,即
。
情况(2):当
时,此时正顾客的有效到达率为
,即当其余所有正顾客都进入系统的情况下,标记顾客选择进入系统后的收益
。故当
时,正顾客的均衡策略为进入队伍,即
。
情况(3):当
时,易验证
在
中有唯一的根。因此,存在唯一的均衡策略
满足
,从而得到:
, (26)
。 (27)
定理2在不可见情形下的带负顾客的Geo/Geo/1排队系统中,当服务费用固定时,企业的最优服务定价决策
为:
。
证明:将公式(26)代入到公式(25),得到:
对
分别求关于
的一阶导数和二阶导数,得到:
,
。
当系统为空时,要确保顾客选择进入系统,要求
,即要求
,故有
。因此
是关于
的凹函数,
存在最大值。令
,从而得到企业的最优服务定价决策
:
。
4.3. 服务费用不固定
这一节将探讨在服务费用不固定的情况下,顾客的均衡策略和企业的最优服务定价问题。在不可见情形下带负顾客的Geo/Geo/1排队系统中,正顾客进入系统后,需缴纳的费用是不固定的,且与平均逗留时间成正比,令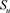 表示单位时间内的服务费用。
表示在服务费用不固定的情况下,正顾客选择进入队伍的均衡概率,因此,均衡到达率
。标记顾客进入系统后的期望净收益用
表示,企业的期望净收益用
表示,则有:
表示单位时间内的服务费用。
表示在服务费用不固定的情况下,正顾客选择进入队伍的均衡概率,因此,均衡到达率
。标记顾客进入系统后的期望净收益用
表示,企业的期望净收益用
表示,则有:
, (28)
, (29)
其中
表示在服务费用不固定的情况下,正顾客在系统中所需的平均逗留时间,且
是有效到达率
的函数。
定理3 在不可见情形下的带负顾客的Geo/Geo/1排队系统中,当服务费用不固定时,顾客的均衡策略
为:
证明:由公式(28)可知:
情况(1):当
时,即
时,此时有效到达率为0,即当其余所有正顾客都不进入系统的情况下,标记顾客选择进入系统后的收益
。故均衡策略为止步,即
。
情况(2):当
时,即
时,此时有效到达率为
,即当其余所有正顾客都进入系统的情况下,标记顾客选择进入系统后的收益
。故均衡策略为进入队伍,即
。
情况(3):当
时,易验证
在
中有唯一的根。因此,存在唯一的均衡策略
满足
,从而得到:
, (30)
。 (31)
定理4 在不可见情形下的带负顾客的Geo/Geo/1排队系统中,当服务费用不固定时,企业的最优服务定价决策
为:
。
证明:将公式(30)代入到公式(29),得到:
对
分别求关于
的一阶导数和二阶导数,得到:
,
。
当系统为空时,要确保顾客选择进入系统,要求
,即要求
,故有
。因此
是关于
的凹函数,
存在最大值。令
,从而得到企业的最优服务定价决策
:
。
4.4. 数值模拟
假定
,
,下面分别分析不可见情形下带负顾客的Geo/Geo/1排队系统中
、
、
对顾客均衡混合策略的影响。
首先分析正顾客的到达率
对均衡混合策略
和
的影响。假定
,
,如图3所示,
和
的曲线相重合且是到达率
的递减函数,即均衡混合策略随着
的增大而减小。曲线相互重合表明,无论服务费用固定与否,顾客的均衡混合策略是一致的,这与文献 [21] 连续时间排队系统的研究结果相一致。此外,当单位时间内到达的正顾客越多,系统越拥挤,顾客的平均逗留时间越长。对应地,此时顾客选择进入系统后其期望净收益越小,因此顾客的均衡混合策略也随之变小。
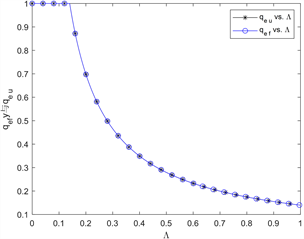
Figure 3. The variation curve of
and
with
in an invisible queuing system
图3. 不可见排队系统中
和
随
的变化曲线
接着分析负顾客的到达率
对均衡混合策略
和
的影响。假定
,
,如图4所示,
和
的曲线相重合且顾客的均衡混合策略随着
的增大,先增大而后减小。显然,当单位时间内到达的负顾客增多,抵消的正顾客也开始增多,能够缓解系统拥挤,此时对于顾客的平均逗留时间也会减小。对应地,顾客选择进入系统后其期望净收益会变大,故均衡混合策略也随之变大。但当
增大到一定程度时,如当
的值超过
时,此时正顾客选择进入系统后被负顾客抵消的概率也非常大,得不到收益,因此顾客的均衡混合策略会变小。

Figure 4. The variation curve of
and
with
in an invisible queuing system
图4. 不可见排队系统中
和
随
的变化曲线
最后分析系统的服务率
对均衡混合策略
和
的影响。假定
,
,如图5所示,
和
的曲线相重合。当
时,顾客的均衡进入概率为0;当
时,顾客的均衡进入概率随着
的增大而增大,直到均衡进入概率为1。从图中显然可知,当单位时间内服务的顾客数增多,越能够缓解系统拥挤,此时对于顾客的平均逗留时间也会减小。对应地,顾客选择进入系统后其期望净收益会变大,因此顾客的均衡混合策略也随之变大。即服务率越高,顾客更愿意选择进入系统。
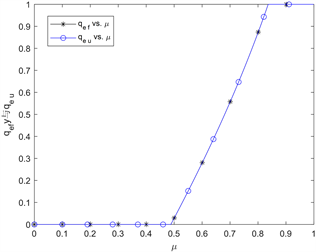
Figure 5. The variation curve of
and
with
in an invisible queuing system
图5. 不可见排队系统中
和
随
的变化曲线
同样假定
,
,下面分别分析不可见情形下带负顾客的Geo/Geo/1排队系统中
、
、
对企业收益的影响。首先分析正顾客的到达率
对企业收益
和
的影响。假定
,
,从图6中能够看出,两种价格机制下,随着正顾客的到达率
不断增大,企业收益
和
仍保持不变,这说明正顾客的到达率
并不会影响企业的最优期望收益。因为当正顾客的到达率发生变化时,企业通过对服务费用进行调整,来改变正顾客的均衡进入概率,从而使得企业的最优期望收益保持不变。此外,从图中也能够发现,服务费用不固定给企业带来的收益要高于服务费用固定带来的收益。这意味着在两种价格机制下,企业更倾向于选择服务费用不固定的定价方式。
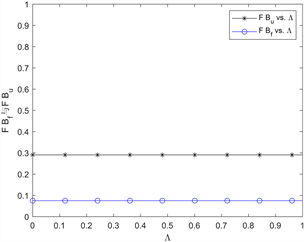
Figure 6. The variation curve of
and
with
in an invisible queuing system
图6. 不可见排队系统中
和
随
的变化曲线
接着分析负顾客的到达率
对企业收益
和
的影响。假定
,
,如图7所示,
和
的曲线在
相对较小时相重合,且企业收益随着
的增大,先增大而后减小。显然,当单位时间内到达的负顾客增多,抵消的正顾客也开始增多,能够缓解系统拥挤,顾客的均衡混合策略也随之变大,顾客更愿意进入系统,因此企业的收益也会随之增加。但当
增大到一定程度时,正顾客选择进入系统后被负顾客抵消的概率也非常大,得不到收益,顾客不愿意进入系统,因此企业的收益也会随之减小。曲线一开始重合说明当
相对较小时,两种价格机制对企业收益的影响是一致的,但当
增大到一定程度时,服务费用不固定给企业带来的收益要高于服务费用固定带来的收益。

Figure 7. The variation curve of
and
with
in an invisible queuing system
图7. 不可见排队系统中
和
随
的变化曲线
最后分析系统的服务率
对企业收益
和
的影响。假定
,
,如图8所示,企业收益是服务率
的递增函数,即企业收益随着
的增大而增大。从图中显然可知,当服务率越高,顾客更愿意选择进入系统,因此企业的收益也会随之增加。此外,从图中也能够发现,服务费用不固定给企业带来的收益同样高于服务费用固定带来的收益。
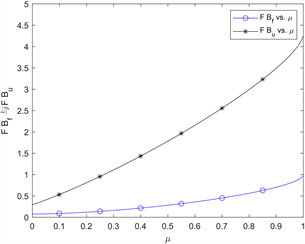
Figure 8. The variation curve of
and
with
in an invisible queuing system
图8. 不可见排队系统中
和
随
的变化曲线
5. 结论
本文研究的模型是带负顾客的Geo/Geo/1排队系统,基于两种价格机制分别对顾客的均衡策略与企业的服务定价做出分析。在可见情形下,通过推导出顾客的平均逗留时间,从而得到顾客的均衡止步策略,并在此基础上利用斯塔克博格博弈模型求得企业的最优服务定价。不可见情形下,通过马尔科夫链与母函数求得稳态下系统的各项指标,最终求得顾客的均衡混合策略与企业的最优服务定价。最后通过数值研究发现,在两种价格机制下,顾客的均衡混合策略是一致的,但企业更倾向于选择服务费用不固定的定价方式。
该研究在理论上将带负顾客的排队策略研究推广到离散时间排队系统当中,并在此基础上考虑了两种价格机制。在实际应用上,能够帮助企业管理者根据不同的价格机制进行最优的服务定价,以使企业能够获得最大的收益,也能够帮助顾客对于是否进入系统做出更理性的决策。未来还可以将带负顾客的Geo/Geo/1排队系统和具有互补性服务的情况相结合,研究系统中顾客的均衡策略和企业的最优服务定价问题。此外,还可以扩展到其他的带负顾客的离散时间排队系统,如带负顾客与多重休假的Geo/Geo/1排队系统、带负顾客与优先权的Geo/Geo/1排队系统等。
基金项目
湖南省教育厅科研项目(20C1521);湖南省大学生创新创业训练计划项目(3031);衡阳师范学院科研启动项目(2023QD25)。
NOTES
*通讯作者。