1. 引言
本文研究如下分数阶Schrödinger-Poisson系统
(1)
正束缚态解的存在性,其中
,
,
,位势
,
和
满足合适的假设。
当
时,问题(1)退化为经典的Schrodinger-Poisson系统,其更一般的形式记为:
 (2)
(2)
该系统出现在量子力学模型和半导体理论中 [1] [2],非线性项
表示粒子的相互作用,
表示与电场的相互作用。
近年来,对于
,
和
的不同假设,很多学者对系统(2)进行了大量的研究,可参见 [3] [4] [5] 等。在文献 [4] 中,作者用热流法证明了当
, 且
时,系统(2)具有指定变号次数的径向变号解。当V为非径向,
,
时,在文献 [3] 和 [5] 中分别证明了
和
时系统(2)存在基态解。
且
时,系统(2)具有指定变号次数的径向变号解。当V为非径向,
,
时,在文献 [3] 和 [5] 中分别证明了
和
时系统(2)存在基态解。
我们记问题(1)的一般形式为
(3)
在文献 [6] 中,当
,
且
具有一般的临界或次临界非线性时,作者证明了径向基态解的存在性。在文献 [7] 中,当 ,
,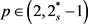 时,作者用Nehari-Pohozaev流形方法证明了正基态解的存在性。在文献 [8] 中,作者研究了当
时,作者用Nehari-Pohozaev流形方法证明了正基态解的存在性。在文献 [8] 中,作者研究了当 ,
时,系统(3)存在基态解和变号解。关于该系统的研究进展可参见 [9] [10] [11] [12] 等等。
,
时,系统(3)存在基态解和变号解。关于该系统的研究进展可参见 [9] [10] [11] [12] 等等。
本文的目的是描述当系数
,
和
竞争时发生的一些现象。为了陈述我们的主要结果,令
其中
和
满足下面的假设:
(H1)
,
,
且
;
(H2)
,
,
且
;
(H3)
,
,
且存在
使得当
时,
此时,问题(1)变为下面的形式:
(4)
就目前的文献来看,关于分数阶Schrödinger-Poisson系统(1),在位势
,
和
满足上述假设的条件下,其束缚态解的研究成果还不多见。本文的目的是推广文献 [13] 中的主要结果到非局部情形。该推广是非平凡的,一方面由于
的非局部性,使得文献 [13] 中的方法不能够直接使用。另一方面,极限方程在无穷远的衰减性是多项式衰减的,而不是指数阶衰减,这会需要更加精细的估计。因此,本文的研究结果更加具有一般性。
下面陈述本文的主要结果:
定理1.1 假设条件(H1)~(H3)成立且
(H4)
,
。则系统(1)存在正束缚态解。
这篇论文的结构如下。在第2节,我们给出了工作空间和准备性引理。在第3节,我们给出了定理1.1的证明。
2. 预备知识
2.1. 工作空间
定义分数阶Sobolev空间
为:
其对应的范数为
接着引入Hilbert空间
,定义为:
其上赋予内积
及对应的范数为
接着,我们介绍要使用到的符号:
·
,
是一个可测集,
表示Lebesgue空间。当O是
的可测子集时,用
表示
的范数;当
时,用
表示
的范数。
·
表示以y为中心R为半径的球;当
时,我们用
来表示。
·
表示不同的正常数。
2.2. 准备性引理
对任何固定的 ,定义泛函
为
,定义泛函
为
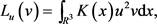
注意到,当
时,
嵌入 ,利用(H3)推得
,利用(H3)推得
因此,
是
上的连续性泛函。应用Lax-Milgram定理,存在唯一的
满足
,且
的表达式如下:
,其中
因此,系统(1)约化为分数阶Schrödinger方程:
(5)
对应于方程(5)的能量泛函定义为:
显然,
并且其临界点是问题(5)的弱解。因此,为了找到系统(1)的解,我们只需找到泛函I的临界点即可,事实上,如果
是I的临界点,那么
就是系统(1)的弱解。
下面给出
的性质 [8]。
引理2.1对任意的
,有
(i)
;
(ii)
;
(iii)
。
证 (i)和(ii)是显然成立的,下面只需证明结论(iii)。由(H3),Hölder不等式和Sobolev嵌入定理有
因此,由上式可得,
。结论(iii)得证。
类似于文献 [14] 中命题2.2的证明,不难证得如下结论:
定理2.2设序列
满足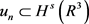 ,如果在
中
弱收敛于u,那么
,如果在
中
弱收敛于u,那么
(i)
在
中;
(ii)
;
(iii)
。
由于泛函I在
中既无上界也无下界,简单计算可知泛函I限制在Nehari流形N上有下界,其中
显然,Nehari流形N包含了泛函I的所有临界点,通常称极小化问题的极小元为极小能量解或基态解。
根据标准的讨论,易证得Nehari流形N具有如下性质:
引理2.3 (i)存在正常数
,使得对于所有的
,
(ii) N是
正则流行且微分同胚于
的球面。
(iii) I限制在N上有正下界。
(iv) u是I在
上的临界点当且仅当u是I限制在Nehari流形N上的临界点。
下面考虑问题(5)对应的极限方程为:
(7)
其对应的能量泛函 定义如下
定义如下
易证
,并记泛函
对应的Nehari流形为
设
由文献 [15] 中的结果知,问题(7)存在唯一正基态解
,满足
,且存在
使得
(8)
对于
的任一变号临界点,下面关系式成立:
(9)
现在,我们考虑约束极小化问题
。我们发现最小能量m与
之间的关系。
引理2.4
且m不可达。
证 设
,则存在
满足
。因此,易得
故
。
下面我们要找到一组序列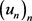 ,
满足
。为此,我们考虑
,
,且当
时,
。设
,其中
满足
,那么
,
满足
。为此,我们考虑
,
,且当
时,
。设
,其中
满足
,那么
由Lebesgue控制收敛定理及假设(H1)~(H3)可推得
结合  ,推出
,其中
是一正常数。因此,由
及
,有
,从而
。
,推出
,其中
是一正常数。因此,由
及
,有
,从而
。
反证法。假设存在
满足
。显然,存在
满足
,经计算得
这说明
且
,因此
且
。
另一方面,由问题(7)的解的唯一性知,存在
,对于每一个
,满足
,也就是说
,矛盾。证毕。
我们试图在
中找到一个高能量水平解,为此,需要下面的全局紧性引理来恢复PS序列的紧性。
引理2.5 ( [12],引理3.1)设
是I限制在N上的PS序列,也就是说,
问题(5)的解为u,子序列仍用
表示,则
要么在
中
成立;
要么在
中
弱收敛于u,且存在整数
,函数列
,点击序列
,
,满足
1) 当
,
时,
,
;
2)
;
3)
;
4)
是问题(7)的非平凡解。
3. 定理1.1的证明
下面我们采用拓扑方法来证明,当(5)没有基态解时,存在更高能量解。设
那么
且在
中连续。令
易证
。定义
如下:
因为
有紧支集,故
的定义有意义且具有以下性质:
1)
在
中连续;
2) 若u是径向函数,则
;
3) 对于所有
,
,有
;
4) 给定
,设
,则
。
由引理2.4我们知道m不可达,借助重心映射
,我们加细Nehari流形,构造新的约束。为此,定义极小化问题如下:

显然,
且下面的严格不等式成立。
类似于文献 [14] 中引理3.3的证明,我们可得:
引理3.1
。
引理3.2 I限制在N上在
中满足PS条件。
证 设
是
的PS序列满足
。由引理2.5,我们有
I的任一临界点v满足
。问题(7)的解u满足
。若u是变号解,则
。故
在
中强收敛。证毕。
令
,
且
。对于
,
,定义
其中
是问题(7)的一个正基态解。存在正数
,
使得
(10)
类似于 [16] 中引理4.4的证明,易得如下结论:
引理3.3 对于所有
,
为了证明
我们做出以下估计。
引理3.4 ( [17],引理A.1)设
且
,那么
利用引理3.4以及假设(H3),可得如下得估计:
引理3.5 对于
且
,
证 根据(8)、(H3)、引理3.4,
那么
下面利用Hölder不等式及(H3)可得:
当
,
时,
,下面利用(8)、(H3)、Hölder不等式及引理3.4,计算得
当
时,
,从而,
又
综上所述,记
,引理3.5得证。
利用引理3.5,很容易推得如下估计:
引理3.6
(11)
根据假设(H4),以及引理3.4,可得如下估计:
引理3.7
(12)
(13)
(14)
证 由(8)及引理3.4有
类似于上面的证明,我们能得到
。
由(8)、引理3.4、(H4)及Hölder不等式,可得
同理可证
。
由
的定义及上面的估算有:
最后类似于上面的证明,易证
。证毕。
类似于 [14] 中引理3.7的证明过程,我们可以得到:
引理3.8
和
如(10)定义,则存在常数C > 0满足
(15)
而且
(16)
基于上面的估计,经计算我们得到下面的关键估计:
引理3.9 存在
满足,对于 ρ > ρ0 ,
证 由引理3.6、引理3.7及引理3.8,
(17)
因为
是(7)的正解,故
直接计算可得
(18)
根据文献 [18] 中的引理2.1,对于
及
有:
那么
(19)
当
或
充分小时,
趋于
或
。那么,此时
。因此,存在
,当
时,
下面我们考虑
时,由(18)和(19)知:
易证下面两个不等式:
因此,
引理3.10 存在
满足
 (20)
(20)
根据
的定义和引理3.1易证上述结果,在此忽略其证明过程。
定理1.1的证明:
由引理2.4我们知道
且m不可达,并且该问题不能通过极小化来解决。因此,我们将通过形变论证来证明系统(1)存在比
能量更高的正解。
对于任意
,定义
。
根据引理3.3,引理3.9和引理3.10得到下列不等式:
下面证明限制在N上的I在水平
上存在PS序列。如果已征得该断言成立,则根据引理3.2知,存在非平凡临界点u且
。
反证法。假设
内不存在PS序列。根据形变引理,存在
和连续映射
,对于
,有
且
。
定义映射
为
。由引理3.10知
。因此
,从而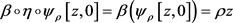 。定义
,其中
。显然,对于
,
有
。于是
,也就是说
。因此,存在
满足
。定义
,其中
。显然,对于
,
有
。于是
,也就是说
。因此,存在
满足
(21)
由引理3.3得
,再根据
的性质,得到
(22)
显然,
,
,特别地,
。结合(21)和
的定义,易知
,与(22)矛盾。
设
是我们找到的临界点满足
。下证u是正函数即不是变号函数。反证法,假设
且
。类似于 [19] 中定理1.2的证明,我们推出,存在
和
满足
。因此,利用引理2.4及上面的事实,可得
这与
相矛盾。证毕。
致谢
国家自然科学基金(No.11501403),山西省留学回国择优项目(2018),和山西省自然科学面上项目(201901D111085)。