1. 概述
时滞是工程实际中广泛存在的一种现象。时滞系统也因此备受学术界关注。其中,时滞系统的稳定性问题是大家关注的焦点 [1] [2] [3] [4]。对于线性系统而言,时滞环节的存在使得系统的动态特性更加复杂,会在一定程度上破坏系统的实际性能,系统的稳定性也因此变得复杂 [5] [6] [7]。
对于线性多时滞离散系统
。 (1)
其中,
是方阵,
为非负整数,N为正整数。对N > 2情形的强稳定性研究,鲜少有文献报道,可能的原因之一是,多时滞问题本身巨大的复杂性,另一原因可能是采用K-L泛函,在处理问题的过程中导致LMI规模异常膨胀。
本文尝试解决N > 2情形下的强稳定性问题。
系统(1)的强稳定性定义由Hale于1993年提出,随后Michiels强化了稳定性的定义,即将系统(1)的稳定分为时滞独立稳定(强稳定)与时滞相关稳定。众所周知,系统(1)的稳定与系统矩阵的谱半径有关,其时滞相关稳定的边界在复平面的单位圆上。文献 [2] 通过解三对解多项式矩阵的正定解来解决这一问题,得到的结论是5个LMI (Linear Matrix Inequality)条件,而LMI是否有解是首先要解决的问题,目前的数值求解方法或多或少具有一定的盲目性。对这一问题较早的研究可追溯到文献 [1] [3] [4]。现有的研究成果大都以充分条件出现,这种判断系统稳定性的准则的优点是计算费用较小,缺点是对某些系统的稳定性检验是失效的。近年来出现了研究系统强稳定的充分必要条件 [5] [6] [8],这一类研究结果避免了检验失效的问题,但计算复杂度是系统矩阵规模的平方,这在系统规模较大时实际计算不可行。
对式(1)进行傅立叶(Fourie)变换,得到系统稳定的充分必要条件为:
。 (2)
式(2)表明,对于稳定的系统,
(
)的特征值不能位于单位圆上。
设
,若存在某一组
使得
,由于谱半径是关于
的连续函数,则必存在某一
值使得
,此时(2)式不成立,系统是不稳定的。
定义1:对系统(1),如果对任何
,(2)成立,则称系统(1)是强稳定的。
考虑到
是关于
的周期函数(周期为
),为方便后文描述,将上述分析概括为下列引理1:
引理1 系统(1)强稳定的充分必要条件为:
。(3)
当Ai为实矩阵时,式(3)的验证区间可缩短
(因为
与
具有相同的特征值集合)。
近年来,关于上述问题的研究,大多采用线性矩阵不等式,但LMI方法计算规模大,计算复杂度以指数形式增长。文献 [5] 给出的算法,其计算复杂度为3n2,而文献 [6] [7] 给出算法的计算复杂度为2n2,虽然与文献 [5] 相比,文献 [6] [7] [8] 的算法有所改进,但并没有从本质上改变计算复杂度,特别是当系统矩阵规模较大时,上述计算将变的不可行。截至目前,关于本专题的研究翰若烟海,感兴趣的读者可以进一步参看综述类文献 [4] [9] [10] [11]。
本文利用二次型与矩阵负定的特性,将矩阵特征值在复平面的分布问题转换为二次型符号的判断问题,进而根据连续周期信号的极值来研究二次型关于参数
在一个周期内的符号变化,并通过二次型在极值点处的值来判断其符号的变化过程,并以此研究时滞系统的稳定和强稳定问题。与以往文献不同的是,本文方法避免了构造泛函的复杂工序,推导过程也不需要复杂的处理技巧,但结论相对简洁,计算复杂度与原矩阵规模一致。
注1:为方便论述,后文中引出下列符号:
表示矩阵X为正定矩阵,
表示矩阵X为负定矩阵,
为虚数单位,
分别表n维向量空间和
维复空间。
表示矩阵的谱半径,
表示矩阵的特征值向量,
表示矩阵的第i个特征值,I为单位矩阵,
表
。
2. 主要研究成果
2.1. 具单时滞系统强稳定的充分必要条件
本节讨论具单时滞系统稳定的条件,它是下一节多时滞强稳定的基础。
二次型的符号与矩阵的特征值有密切关系,如下列引理2所示:
引理2 对任一非零
,二次型
的充分必要条件为
。
对于含有连续参数的二次型,为了判断二次型的符号,根据连续函数的性质,可以求得二次型关于参数的驻点,如果所有驻点处的二次型函数值均小于零,则可以断定参数矩阵是稳定的。
引理3 设A具有线性无关的特征向量,
,是矩阵A的非零特征值,
为非零特征值的个数。二次型为:
, (4)
取极值的条件为:
。 (5)
证明:令
,有
。 (6)
设
是A的一组线性无关的单位正交特征向量,则任一向量x可表示为
。于是有
,进一步得到
, (7)
将式(7)代入式(6)可得:
。
化简上式,得到
,由于x为任意非零向量,
具有任意性,故(5)式成立。引理证毕。
定义2:称满足式(5)的相位角
的集合为脆弱相位集,并记为
,脆弱相位对应的系统称为脆弱系统。
脆弱系统包含了系统时滞导致系统最坏稳定状态的情形,当脆弱系统稳定时,系统在各种不同时滞影响下必稳定。
引理4 线性离散系统
,(8)
强稳定的充分必要条件是
。 (9)
式中
,P是正定矩阵,满足
。 (10)
证明:考虑下列二次型
,
展开上式可得:
。
由引理3可知,
在一个周期内所有可能的极值点为:
。对任
取
,若
,因
为极值,故
。由引理1可知,若条件成立,必有
。 (11)
这等价于式(9)成立。定理证毕。
注2:计算
的特征值需要先指定正定阵P,从计算简单考虑初始矩阵可以取为单位矩阵I,或者通过解离散Lyapunov方程
来设定。可能此初定的P不能满足式(10),但若此时条件(9)成立,由离散Lyapunov理论可知,一定存在某个正定阵P使式(10)成立,可由解LMI(10)获取P,并用来代替P的初始矩阵。重复以上步骤,直到得到结论。定理1的算法整个流程可概括如下:
Step1:设定P;
Step2:计算特征值对应的相角
;
Step3:检查式(9)是否成立,如成立转Step4,如不成立,系统非强稳定,停止;
Step4:检查式(11)是否成立,如是,系统强稳定,停止。否则按(10)使用MATLAB的dlyap函数,计算P,转Step2。
当
的所有非零特征值为实数时,
,于是有下面的推论:
推论1 设
,若存在正定阵P满足
, (12a)
或
, (12b)
使
所有非零特征值为实数,则离散系统(8)强稳定的充分必要条件为:
。 (13)
注3:对于N = 2的情形,已有文献的结论表明,需要在
的规模上验证LMI。而本文引理4至多需要计算n个常数矩阵的谱半径,更确切地说,实际上只需要计算矩阵
的非实数特征值个数;当
为实矩阵时,考虑到实矩阵的复数根是共轭的,则计算量减半。值得一提的是,当n较大时,计算谱半径不是件容易的事,由
,可用范数来代替谱半径,这种处理手段以牺牲保守性为代价,但可以降低计算复杂度。
2.2. 多时滞系统强稳定的充分必要条件
定理1 系统(1)是强稳定的,当且仅当存在正定矩阵
,满足
,
,使
,for
, (14)
这里
。
证明:本证明采用数学归纳法。
设
,当k = 1,2时,由引理4知,结论成立,假设k = i时,定理成立,现考虑k = i+1的情形。
考虑二次型:
,
。
令上式等于0,得到
,用脆弱系统
代替
,然后利用引理4同样的技术,可知结论成立。
因此k = i时,定理依然成立,由归纳法原理,定理对所有
都是成立的。定理证完。
3. 数值释例
本节采用经典的数值例子来解释本文结果的应用。例1解释引理4的应用,例2解释正定矩阵P的确定过程,例3是一个以往文献常采用的实例,这里我们给出了不一样的结论。
例1 [8] 考虑系统(8),其中
。
取
,计算可得:
,显然
有2个线性无关的特征向量,可由推论1讨论其稳定性。容易验证
,故
是满足式(12b)的,又
,由引理4知,系统是强稳定的。图1是例1在一周期内,谱半径的变化过程,所有谱半径均小于1,说明本文结果是正确的。

Figure 1. Example 1 Spectral radius change in one period
图1. 例1在一个周期内的谱半径变化
下面例2解释正定矩阵P的确定过程。
例2 [5] 考虑系统(1),其中
。
取
,计算
。对于
,
非负定,但
。故P的选择不当,解下列矩阵方程(在式(12b)中右端选择负定阵-I):
,可以得到
。
重新计算
,容易验证
,故P为所求。进一步由推论1,
,故系统是强稳定的。
例3 ( [12],例2)考虑离散系统(1),其中
,
。
1) 对c = 1,取
,计算可得:
,显然
有2个线性无关的特征向量,计算有
,
,
。容易验证,
,由定理1可知,系统是强稳定的。
2) 对c = 1.2,取
,计算可得
,
,
,由此判断系统不是强稳定的。
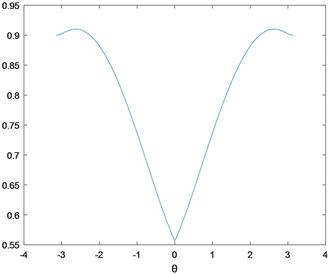
目前,针对上述案例,文献 [12] [13] [14] [15] 的结论均表明系统不是强稳定的,而本文的研究表明系统是强稳定的。图2给出了系统矩阵
在c = 1时,一个周期内的谱半径的变化情况,从图上可以看出,该系统对应的谱半径小于1,表明系统确实是强稳定的。图3为c = 1.2的情形,可以看出,系统矩阵
存在大于1的谱半径(事实上,
),故系统不是强稳定的。
 (a)
(a)  (b)
(b)
Figure 2. (a) Spectral radius of the example 3 for c = 1; (b) Spectral radius of the example 3 for c = 1.2
图2. (a) 例3的谱半径曲线(c = 1);(b) 例3的谱半径曲线(c = 1.2)
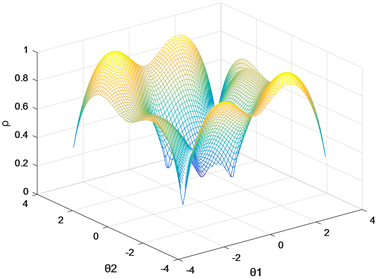
Figure 3. The range of system matrix spectral radius change of the Example 4
图3. 例4系统矩阵谱半径变化范围
例4 [16] 考虑系统(1),其中
。
对c = 1,按下列步骤分析稳定性:
Step1:因为
,选择P为下列离散Lyapunov方程的解:
,解得
,计算
,得
,
。
脆弱相位为
,注意到
,由推论1知第一个两路径反馈系统是稳定的。
Step2:计算
,
,按第一步同样的方法,可得
,计算
,
,
,
。
经计算,可以得到
,由定理1知,系统是强稳定的。
图3给出了一个周期内系统矩阵谱半径的范围,由图3可知,所有谱半径均小于1,系统确实是强稳定的。
4. 结论
本文以二次型极值方法讨论了离散线性时滞系统的强稳定(时滞无关稳定)及时滞相关稳定性问题。将单时滞离散系统的稳定问题转换为二次型极值问题,通过极值的符号建立系统矩阵特征值在复平面上的分布关系。论文还讨论了系统时滞相关稳定的问题,提出了时滞边界的估计方法。所得结论为充分必要的,因而不存在保守性问题。从结果看,与现有方法相比,本文提出的方法较大程度地减少了计算量,稳定性的判别条件也更为简单。数值实例也验证了本文方法的有效性和可行性。此外,本文所提的方法可进一步推广到控制器的设计以及多时滞系统的稳定性判断等研究中。
NOTES
*通讯作者。