电磁作用实现由方波簇到调幅峰的转迁

Realizing the Transition of Electromagnetic Action from Square Wave Bursting to Amplitude-Modulation Spiking

摘要: Pre-Bötzinger复合体是哺乳动物产生呼吸节律的脑干区域。磁通控制忆阻器用于连接膜电位和磁通量。在Butera动力学模型的基础上引入忆阻器，研究电流和磁流对神经元放电模式的影响及其产生的动力学机理。结果表明，电流和磁流作用都可以使pre-Bötzinger复合体放电模式由方波簇转迁到混合簇，再转迁为调幅峰。

Abstract: The pre-Bötzinger complex in the brainstem region can generate respiratory rhythm in mammals. The magnetic flux-controlled memristor is used to bridge the membrane potential and the magnetic flux. By adding the magnetic flow to Butera’s neuron model, we study how the electric current and magnetic flux influence neuronal activities and its dynamic mechanism. The results show that both electric current and magnetic flux can transform the firing patterns of the pre-Bötzinger complex from square wave bursting to mixed bursting, and then amplitude modulation spiking.

1. 引言

神经科学是一门综合性学科，可以对动物和人类的神经系统进行生物学研究。随着神经实验和计算技术的发展与创新，神经科学研究取得了长足的进步。为了全面而深入地了解大脑活动的规律性，人们已经深刻认识到建立神经科学理论体系的重要性。Pre-Bötzinger复合体(pre-BötC)是兴奋性耦合的神经元网络。实验发现pre-BötC对呼吸节律的产生至关重要 [1]，pre-BötC内的单个神经元会表现出复杂的放电节律模式 [2] [3] [4]。神经元电活动表现为振荡脉冲，包括静息态(resting state)、峰放电(spiking)和簇放电(bursting)。

非线性动力学是研究非线性动力系统中各种运动状态的定量和定性规律，特别是运动模式演化行为的科学。一般来说，非线性科学的主体包括混沌、分岔、孤立子和斑图等。其中，分岔和混沌是两个最基本的非线性现象，由于它们的主要特点是在动力学的基础上去揭示事物非线性本质特性，所以它们成为了非线性科学研究领域中的活跃主题。Rinzel [5] 引入了快慢分析法，将相关研究提升到机理分析的层次，其中心思想是：将不同尺度耦合系统分解为相互耦合的快慢两个子系统，通过对快子系统的平衡态及其分岔分析，得到静息态和放电态之间相互转化的分岔机制，从而揭示相应簇放电的产生机理。神经元的放电模式及不同模式间的转迁能够通过数值模拟和分岔理论进行解释 [6] [7] [8] [9]。

电活动是普遍存在的神经元生物电现象，它有许多不同的模式来编码生物信息的表达，构成神经元之间信号传播的整个过程。近年来，电流和磁流对神经元放电活动的影响引起科学家的关注 [10] [11] [12]。忆阻器具有记忆性的特点，可用其模拟神经元突触的可塑性。本文在考虑钙激活的非特异性阳离子电流(I_CAN)和持续钠电流(I_NaP)的情况下，在Butera动力学模型中考虑磁通控制忆阻器的影响，研究电流和磁流对单个pre-BötC神经元放电模式的影响，并用峰峰间期(InterSpike Interval, ISI)和分岔分析解释其产生和转迁的动力学机理。研究结果为深入了解电磁辐射对神经元放电模式的影响提供有益的探讨。

2. 模型描述

为了研究电流和磁流对pre-BötC神经元活动的影响，我们在Butera [13] 提出的pre-BötC单室细胞模型中引入了电流和磁通控制忆阻器。模型描述如下：

$\frac{\text{d}V}{\text{d}t}=\left(-I_L-I_{\text{K}}-I_{\text{Na}}-I_{\text{NaP}}-I_{\text{tonice}}-I_{\text{CAN}}+I-k_{1}V\rho \left(\phi \right)\right)/C$ (1)

$\frac{\text{d}n}{\text{d}t}=\left(n_{\infty }\left(V\right)-n\right)/{\tau }_n\left(V\right)$ (2)

$\frac{\text{d}h}{\text{d}t}=\left(h_{\infty }\left(V\right)-h\right)/{\tau }_h\left(V\right)$ (3)

$\frac{\text{d}\phi }{\text{d}t}=V-k_2\phi$ (4)

钙动力学为：

$\frac{\text{d}\left[\text{Ca}\right]}{\text{d}t}=f_m\left(J_{{\text{ER}}_{\text{IN}}}-J_{{\text{ER}}_{\text{OUT}}}\right)$ (5)

$\frac{\text{d}l}{\text{d}t}=A{K}_d\left(1-l\right)-A\left[\text{Ca}\right]l$ (6)

在方程(1)中，V是膜电位，C是膜电容，t是时间。I_L, I_K, I_Na, I_NaP, I_tonice和I_CAN分别代表漏电流，钾电流，快速钠电流，持续钠电流，兴奋性刺激产生的电流和钙激活的非特异性阳离子电流。I是外部刺激的直流电。 $k_{1}V\rho \left(\phi \right)$ 可用于描述电磁感应引起的感应电流：参数k₁对膜电位上的电流起到调节作用， $\rho \left(\phi \right)$ 是指磁通控制忆阻器的记忆电导，用来描述磁通量 $\phi$ 与V之间的关系，其表达式为：

$\rho \left(\phi \right)=\frac{\text{d}q\left(\phi \right)}{\text{d}t}=\alpha +3\beta {\phi }^2$，其中 $\alpha$， $\beta$ 是固定的参数值。定义 $I_{app}=I-k_{1}V\rho \left(\phi \right)$ 来表示由电流和磁流引

起的外激励总和。方程(1)右边各离子电流描述如下：

$I_{\text{L}}=g_{\text{L}}\left(V-V_{\text{L}}\right)$， $I_{\text{K}}=g_{\text{K}}{n}^4\left(V-V_{\text{K}}\right)$，

$I_{\text{Na}}=g_{\text{Na}}{m}_{\infty }^3\left(V\right)\left(1-n\right)\left(V-V_{\text{Na}}\right)$， $I_{\text{NaP}}=g_{\text{NaP}}m{p}_{\infty }\left(V\right)h\left(V-V_{\text{Na}}\right)$，

$I_{\text{tonice}}=g_{\text{tonice}}\left(V-V_{\text{syn\_e}}\right)$， $I_{\text{CAN}}=g_{\text{CAN}}f\left(\left[\text{Ca}\right]\right)\left(V-V_{\text{Na}}\right)$，

$f\left(\left[\text{Ca}\right]\right)=1/\left(1+{\left(K_{\text{CAN}}/\left[\text{Ca}\right]\right)}^{n_{\text{CAN}}}\right)$。

方程(2)和(3)中的n和h是电压门控钾和钠通道的门控变量，且这两个方程以及离子电流表达式中出现的平衡函数 $n_{\infty }\left(V\right)$, $h_{\infty }\left(V\right)$, $m_{\infty }\left(V\right)$, $m{p}_{\infty }\left(V\right)$ 可表示为： $x_{\infty }\left(V\right)=1/\left(1+\exp \left(V-{\theta }_x/{\sigma }_x\right)\right),x\in \left\{n,h,m,mp\right\}$。方程(2)和(3)中所涉及的时间尺度函数表达式为： ${\tau }_x\left(V\right)={\bar{\tau }}_x/\cosh \left[\left(V-{\theta }_x\right)/2{\sigma }_x\right],x\in \left\{n,h\right\}$。

方程(4)中的 $\phi$ 表示跨膜的磁通量，可以描述电磁感应和磁场的影响。k₂用来抑制磁通量的增加。根据法拉第电磁感应定律和忆阻器的描述，电荷对磁通量的依赖性由记忆电导定义如下：

$i^{\prime }=\frac{\text{d}q\left(\phi \right)}{\text{d}t}=\frac{\text{d}q\left(\phi \right)}{\text{d}\phi }\frac{\text{d}\phi }{\text{d}t}=k_{1}V\rho \left(\phi \right)$。方程(1)-(4)构成胞体子系统。

方程(5)和(6)组成细胞内的钙动力系统，可以认为是细胞内的树突子系统。方程(6)中的l表示ER膜中尚未灭活的IP₃通道比例，这取决于细胞内钙浓度([Ca])。方程(5)指定[Ca]是由从胞浆( $J_{{\text{ER}}_{\text{IN}}}$ )进入内质网的通量和从内质网进入胞浆( $J_{{\text{ER}}_{\text{OUT}}}$ )的通量决定的。这些通量受细胞内IP₃的浓度[IP₃]以及IP₃通道门控变量l的调节，并表示为

$J_{{\text{ER}}_{\text{IN}}}=\left(L_{{\text{IP}}_3}+P_{{\text{IP}}_3}{\left[\frac{\left[{\text{IP}}_3\right]\left[\text{Ca}\right]l}{\left(\left[{\text{IP}}_3\right]+K_I\right)\left(\left[\text{Ca}\right]+K_a\right)}\right]}^3\right)\cdot \left({\left[\text{Ca}\right]}_{\text{ER}}-\left[\text{Ca}\right]\right)$，

$J_{{\text{ER}}_{\text{OUT}}}=V_{\text{SERCA}}\frac{{\left[\text{Ca}\right]}^2}{K_{\text{SERCA}}^2+{\left[\text{Ca}\right]}^2}$。

假设细胞内的钙总量([Ca]_Tot)是恒定的。在此假设下，[Ca]_ER可按如下方式计算：

${\left[\text{Ca}\right]}_{\text{ER}}=\frac{{\left[\text{Ca}\right]}_{\text{Tot}}-\left[\text{Ca}\right]}{\sigma }$。

方程(1)~(6)组成全系统。模型中的参数取值见表1。

Table 1. Parameter values in the theoretical model

表1. 模型中的参数值

实验证实了持续钠电流(I_NaP)和钙激活的非特异性阳离子电流(I_CAN)在pre-BötC神经元中普遍存在，并在神经元节律脉冲中起着重要的作用 [14] [15]。上述数学模型可以展示持续钠电流和钙激活的非特异性阳离子电流两种电流的共同作用，是包含I_NaP和I_CAN在内的简化了的一个完整的单室pre-BötC吸气神经元模型。此模型更为简单且与实验中观察到的pre-BötC神经元电生理记录的振荡脉冲的许多动态特征一致，包括电压依赖性活动模式(静息、峰放电和簇放电)。模型的鲁棒性与结果的稳定性已得到证实 [16] [17]。基于上述模型的分析及计算结果能更好的帮助我们来理解一些实验结果背后的机制并指导实验的测量。

除了pre-BötC神经元的呼吸网络外，树突状钙振荡与体细胞之间的相互作用可能发生在大脑区域的各种神经元中，包括丘脑皮质神经元、新皮质神经元和海马体中间神经元以及小脑颗粒细胞。因此，本文的研究可应用于其他类神经元细胞模型中。

3. 无外界刺激( $I_{app}=0$ )时神经元的放电模式和分岔分析

当外激励 $I_{\text{app}}=0$ 时，系统的簇放电模式如图1(a)所示。黑色实线是膜电位V随时间t的变化过程，红色虚线是细胞内钙浓度[Ca]随时间t的变化过程。此时系统呈现方波簇。

在系统中，V，n和 $\phi$ 是快变量，h和[Ca]是慢变量，l是超慢变量。选择慢变量[Ca]作为快子系统的分岔参数，并对h取平均值(h = 0.4192)进行分岔分析。为方便起见，用 $g_{\text{CANTot}}=g_{\text{CAN}}f\left(\left[\text{Ca}\right]\right)$ 代替[Ca]作为分岔参数，其中 $f\left(\left[\text{Ca}\right]\right)$ 是单调递增函数。快子系统对慢变参数 $g_{\text{CANTot}}$ 的分岔如图1(b)所示。平衡点形成S形曲线(黑色实线)，曲线的下分支和中支分别由稳定结点和不稳定鞍点组成。曲线的上分支由稳定和不稳定的焦点组成，不稳定焦点经由Hopf分岔(subH)变为稳定焦点，并在Hopf分岔处产生极限环(红色实线)。点F₁和F₂表示平衡点的鞍结分岔。全系统在( $g_{\text{CANTot}}$，V)平面上的轨线(绿色曲线)也叠加在分岔图上。当 $g_{\text{CANTot}}$ 增大时，S型曲线下支的静息态经由平衡点的鞍结分岔F₁跃迁至上支的稳定极限环，并由于极限环的吸引反复振荡，振荡态最终跃迁至下支的静息态，从而完成了一个周期振荡。根据Izhikevich簇放电分类的标准 [18]，此时的簇放电模式为“fold/homoclinic”型簇放电。

Figure 1. Firing patterns and bifurcation analysis when $I_{\text{app}}=0$. (a) Time series of the membrane potential; (b) Fast-slow decomposition and bifurcation analysis

图1. $I_{\text{app}}=0$ 时的簇放电模式和分岔分析。(a) 膜电位V的时间序列；(b) 分岔分析

4. 电流对神经元放电模式的影响及分岔分析

本节研究电流对混合簇的影响。当 $k_1=0.1$， $k_2=3{\text{s}}^{-1}$， $\alpha =1\text{M}{\Omega }^{-1}$， $\beta =0.00006\text{M}{\Omega }^{-1}\cdot {\text{V}}^{-2}\cdot {\text{s}}^{-2}$ 时，不同电流值所对应的簇放电模式如图2所示。黑色实线是膜电位V随时间t的变化过程，红色虚线是细胞内钙浓度[Ca]随时间t的变化过程。

当 $I=-2\text{μA}$ 时，外激励电流的值比较小，与无外界刺激时的放电状态类似，系统呈现方波簇放电，如图2(a)所示。当电流I的值分别为5 μA, 10 μA, 15 μA时，系统产生胞体－树突簇(somato-dendritic bursting)，是一种特殊的混合簇，分别如图2(b)~(d)所示。此种胞体-树突簇与实验中观察到的一种叹息簇 [19] 非常类似。随着电流的增大，两个簇之间的静息态逐步变为峰放电状态，导致混合簇中胞体部分尖峰的个数逐渐增多。当电流I的值增大为20 μA时，两簇之间的静息状态消失，全部表现为尖峰放电态，参照调幅簇(AMB) [20] 的命名方式，我们称此时的放电状态为调幅峰 [21] 放电。峰放电振幅的变化是由[Ca]波动引起的，如图2(e)所示。

Figure 2. Different firing patterns under different electric currents. (a) $I=-2\mu \text{A}$ ; (b) $I=5\mu \text{A}$ ; (c) $I=10\mu \text{A}$ ; (d) $I=15\mu \text{A}$ ; (e) $I=20\mu \text{A}$

图2. 不同电流值下的簇放电模式。(a) $I=-2\mu \text{A}$ ；(b) $I=5\mu \text{A}$ ；(c) $I=10\mu \text{A}$ ；(d) $I=15\mu \text{A}$ ；(e) $I=20\mu \text{A}$

峰峰间期，即ISI序列能够展现从方波簇到混合簇再到调幅峰的复杂转迁规律。取对数后的ISI序列随电流I的变化情况如图3所示。随着电流的增大，两簇之间由原来静息的状态逐步变为尖峰放电状态，导致前一个簇结束的时间与后一个簇开始的时间之间的间距逐渐变小，直至消失，全部变为峰放电状态，对应最大ISI逐渐降低。

Figure 3. The change of ISI sequence with current I

图3. ISI序列随电流I的变化情况

将不同电流值下的簇放电模式在( $g_{\text{CANTot}}$，V)平面上的轨迹叠加到快子系统的分岔图上，如图4(a)~(e)所示。平衡点形成S形曲线，其他字母及曲线表示的含义与图1(b)相同，且簇放电模式均为“fold/homoclinic”型簇放电。

Figure 4. The bifurcation of the fast system under different current values, the illustration is a partial enlargement. (a) $I=-2\mu \text{A}\left(h=0.3692\right)$ ; (b) $I=5\mu \text{A}\left(h=0.2669\right)$ ; (c) $I=10\mu \text{A}\left(h=0.2004\right)$ ; (d) $I=15\mu \text{A}\left(h=0.1404\right)$ ; (e) $I=20\mu \text{A}\left(h=0.0919\right)$

图4. 不同电流值下的快子系统的分岔，插图是局部放大。(a) $I=-2\mu \text{A}\left(h=0.3692\right)$ ；(b) $I=5\mu \text{A}\left(h=0.2669\right)$ ；(c) $I=10\mu \text{A}\left(h=0.2004\right)$ ；(d) $I=15\mu \text{A}\left(h=0.1404\right)$ ；(e) $I=20\mu \text{A}\left(h=0.0919\right)$

5. 磁流对神经元放电模式的影响及分岔分析

下面我们固定 $I=0$，设置参数 $k_2=3{\text{s}}^{-1}$， $\alpha =1\text{M}{\Omega }^{-1}$， $\beta =0.00006\text{M}{\Omega }^{-1}\cdot {\text{V}}^{-2}\cdot {\text{s}}^{-2}$，研究磁流反馈系数 $k_1$ 对簇放电模式的影响。不同 $k_1$ 值所对应的簇放电模式如图5所示。黑色实线是膜电位V随时间t的变化过程，红色虚线是细胞内钙浓度[Ca]随时间t的变化过程。其中，图5(a)是方波簇，图5(b)和图5(c)为胞体–树突簇，图5(d)是调幅峰。与电流作用效果相类似，增大磁流也可以实现由方波簇到混合簇，再到调幅峰的转换。

Figure 5. Different firing patterns under different $k_1$ values. (a) $k_1=0.01$ ; (b) $k_1=0.2$ ; (c) $k_1=0.4$ ; (d) $k_1=0.6$

图5. 不同 $k_1$ 值下的簇放电模式。(a) $k_1=0.01$ ；(b) $k_1=0.2$ ；(c) $k_1=0.4$ ；(d) $k_1=0.6$

取对数后的ISI序列随参数 $k_1$ 的变化情况如图6所示。与ISI序列随电流I的变化情况类似，随着参数 $k_1$ 的增大，两簇之间由原来静息的状态逐步变为尖峰放电状态，导致前一个簇结束的时间与后一个簇开始的时间之间的间距逐渐变小，直至消失，最后全部变为峰放电状态，对应最大ISI逐渐降低。大约在 $k_1=0.5$ 时簇放电转变为峰放电。

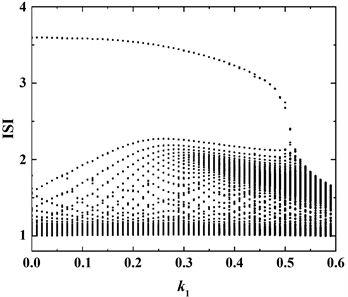
Figure 6. The change of ISI sequence with parameter k₁

图6. ISI序列随参数k₁的变化情况

6. 结论

神经动力学是研究神经系统的动力学与控制问题的重要理论基础，涉及脑神经电生理、信息和认知活动的动力学建模和行为分析等，是国际前沿研究领域。本文主要应用ISI序列以及快慢变量分岔分析的方法，研究电磁流对神经元放电模式的影响。结果表明，电流和磁流都可以实现由方波簇到调幅峰的转迁。在转迁过程中，随着外激励强度的不断增加，两簇之间的静息状态逐步变为峰放电状态，导致一种特殊的混合簇：胞体–树突簇的出现。外激励强度继续增加会导致原来两簇之间静息态完全消失，全部转变为峰放电状态。由于[Ca]的波动，峰放电之间振幅有所不同，我们称此时的放电状态为调幅峰放电。这一系列过程即是由于外激励强度增加，导致系统放电状态由方波簇到混合簇再到调幅峰的转迁的过程。利用ISI序列展现由方波簇到调幅峰转迁的复杂过程，随着外激励增加，最大ISI序列的逐渐降低对应两簇之间静息态持续时间的逐渐减少。分岔分析图中全系统轨线与时间序列图中的簇放电状态能够很好的对应，进一步解释了这一转迁背后的动力学机理。

调幅峰现象较为新颖，之前的研究极少出现，本文实现了由方波簇到调幅峰的转换，并揭示其背后的动力学机理，为神经动力学行为添加了新的示例，进一步丰富了非线性动力学行为的内容。以往的研究多关注离子电导的影响及两个细胞的耦合、同步等现象，而本研究则关注电磁作用的影响。研究结果有助于了解电磁流作用的动力学机理，为神经系统疾病的预防和治疗提供一定的理论支持。

基金项目

本文得到国家自然科学基金(项目编号：11872003)及北方工业大学“特色学科建设”项目(项目编号：110052972027/014)的资助。

NOTES

^*通讯作者。