1. 引言
在传染病的数学模型中,最早Kermack和Mckendrick在1927年提出了一个著名的SIR“仓室”模型。所谓SIR仓室模型就是针对某类传染病将该地区的人群分成三个仓室
。
表示t时刻未染病但有可能被该类传染病传染的人数,
表示t时刻已被感染成病人而且具有传染率的人数,
表示t时刻已从染病者类移出的人数。而且他们假设此环境的总人口保持一个常数,假设一个病人一旦与易感者接触就必然具有一定的传染力,而且一个病人能感染的易感者数目与此环境内的易感者总数成正比。很显然这种假设太简单,后来Capasso和Serio在对1973年巴里(意大利东南部港市)发生的霍
乱这一地方病传播的研究后引入一种饱和的传染率
,其中,
这种传染率的重要性在于染病者和易感者的有效接触数量将随着人群的拥挤作用或易感者采取保护措施而出现饱和、甚至下降。
文献 [1] 考虑具有饱和发生率
的传染病模型,文献 [2] 采用了当
的情况,研究了人类免
疫缺陷病毒1型和丙型肝炎病毒,文献 [3] 讨论了当
时的SIRS型传染病模型,并分析了这类模型的分支情况,文献 [4] - [14] 同样也研究了饱和发生率的传染病模型。
基于此,本文将研究具有代表意义的具有常数输入且疾病发生率为非线性的动力系统模型,以期为进一步理解种群动力学和流行病动力学的机理提供支撑,并提出一种新传染率下的SIRS模型,对模型应用数值模拟方法,研究解的稳定性,以及重要参数对稳定性的影响。
2. 传染率为
的新的SIRS模型
2.1. 基本模型与假设
将所研究的种群分为易感者、染病者和恢复者三类,以
、
和
分别表示t时刻易感者、染病者和恢复者的数量,建立模型的基本假设为:
1)
表示对种群的常数输入率,且均为易感染者;
2)
表示种群的自然死亡率,与种群数量N有关,满足
,
;当种群中无传染病存在时,种群(N)的变化率符合方程
;
3)
表示染病者的因病死亡率;
4)
表示染病者的恢复率;
5)
表示恢复者的免疫失去率,即恢复者中一部分人将失去免疫力,从而又成为易感者;
6) 通过有效接触传染病传播的传染率为
。
用框图表示上述传染病假设的传播规律如下:

根据上述仓式框图建立模型:
(2-1)
2.2. 模型的分析
由于
,所以有,
做变量替换:
,(2-2)
则
分别表示t时刻易感者、感染者和治愈者在种群中多占的比例。直接计算可得:
(2-3)
和
(2-4)
根据模型的实际意义,设模型(2-3)和(2-4)的初始条件为
由
有
。将
代入系统(2-3)的第二个方程可得:
(2-5)
显然,
是模型(2-5)的解。有解的存在惟一性知:当初值
时,对于
都有
,进而由模型(2-3)的第一个和第三个方程有
,
,所以模型(2-5)有正不变集
2.3. 模型求解的Matlab实现
记控制传染病的阈值
,当
该模型(2-5)有无病平衡点
,且在该
点是全局渐近稳定的,模型的解应是趋向于无病平衡点的。
给定新模型的初值和参数如下:
初值:
时,
参数:
,
,
,
,
,
。
有
与
的关系不难求出当
时,模型的解在P0点是全局渐近稳定的;当
时,该模型的解趋向于另一个点P1 (此处不做具体研究),但是此时在P0点不是全局渐进稳定的。
下面对当
时运行本文中编写的4阶R-K [15] 程序,并用所得到的数据画图,见图1和图2:

Figure 1. Time-varying image of susceptible S
图1. 易感者S随时间的变化图像

Figure 2. Time-varying image of susceptible patient I and healer R
图2. 染病者I和治愈者R随时间的变化图像
从上面的图像中不难看出,随时间变化,染病者和恢复者占总人口数的比例趋向于零,而易感染者所占比例趋向于1,即此时,模型的解趋向于无病平衡点。
增大
的值使
,不妨取
,运行程序,同样用得到的数据作图,见图3和图4:
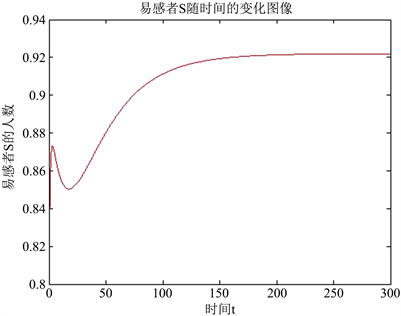
Figure 3. Time-varying image of susceptible S
图3. 易感者S随时间的变化图像

Figure 4. Time-varying image of susceptible patient I and healer R
图4. 染病者I和治愈者R随时间的变化图像
从图像中以看出,此时模型的解并不趋向于点
,即模型的解在无病平衡点是不稳定的;但是从图像中可以看出模型的解趋向于另一个点
,该点可能就是地方病平衡点。
2.4. 结论
从上述两次数值模拟中可以看到,如果取
,则感染者和治愈者所占比例均趋向于零,而易感染者比例趋向于1,故传染病没有蔓延;但是当
,感染者和治愈者所占比例均不趋向于零,故传染病可能会蔓延。
所以,在本模型给定上述参数不变的情况下,控制
即可有效的控制传染病,避免传染病的蔓延。
3. 总结
本文主要研究的是在传染病模型中其他参数不变的前提下通过控制传染病的阈值
确定一个重要参数
的范围,从而验证无病平衡点的全局渐近稳定性。
另外考虑增大和减小
的值,观察传染病模型解的趋向变化。
新的SIRS传染病模型是在已有的经典传染病模型基础上的改进,同样由
给出
的一个范围,使新的传染病模型的解在无病平衡点是全局稳定的,并且从图像中观察传染病模型解的趋向;另外给出一个使
的
值,同样作图,通过对比两次数值实验,可以看出两个
值使模型的解呈现两种趋向,从而比较传染病是否蔓延的两种状态。