1. 引言
设
是
中的光滑有界区域,
,
是
中的标准单位球,
。定义映射
的非局部能量为
(1)
我们称(1)的临界点为s-阶调和映射。令
表示
的边界,
表示
在函数空间
中的Frechet导数,即:对任意的
和
,
这里,
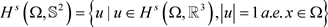
且
于是具有固定边值条件的s-阶调和映射方程为:
 (2)
(2)
这里
是一个固定的函数且对几乎处处的
,
。
设
,其中,
是无边的k-维光滑子流形。如果函数u是泛函
在扰动
下的临界点,则称u为s-阶调和映射。其中,
,
是
到子流形
上的投影映射。当s = 1时,这是经典调和映射的概念,文献 [1] [2] 和 [3] 对调和映射的当前研究情况进行了系统的总结。近些年以来,人们对s为非整数的情形非常感兴趣,比如当靶流形
为标准黎曼球面时,文献 [4] 利用三交换子估计方法,证明了1/2-阶调和映射的光滑性;文献 [5] 得到了n/2-阶调和映射的光滑性;文献 [6] 分析了1/2-阶调和映射的紧致性和爆破性质;文献 [7] 证明了n/2-阶调和映射的Hölder连续性。当靶流形
为一般的紧致黎曼流形时,文献 [8] 得到了1/2-阶调和映射的Hölder连续性。文献 [9] 证明了靶流形分别为球和黎曼齐次流形时积分微分调和映射热流整体弱解的存在性。Alouges在文献 [10] 给出了一类经典调和映射能量极小问题的迭代算法,文献 [11] 讨论调和映射逼近格式的稳定性和收敛性,介绍了一种基于Alouges的迭代算法的有限元离散化方法,并证明了它仅对锐角型三角剖分是稳定和收敛的,并提出了一个后验准则,使我们能够得到一般三角剖分上调和映射弱收敛的充分条件和自适应网格细化的充分条件,数值模拟实验进一步表明,自适应策略可以自动细化典型奇异点附近的三角剖分,从而提高其运算效率。
在本文中,基于能量泛函(1)极小化问题,我们对s-阶调和映射(2)提出一类迭代算法,将经典的Alouges算法 [10] 推广到分数阶方程的情形(2)。具体地,我们有:
算法1 设
,对
,直至收敛,第一步,定义
= {
使得
几乎处处成立},求解极小值问题
(3)
设
为此问题的解。第二步,令
。
在算法1中,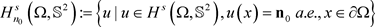 。于是我们有以下定理:
。于是我们有以下定理:
定理1 算法1中的序列
在
中弱收敛到s-阶调和映射
。进一步,
在
中强收敛到
。
注记1 在(2)两边同时取内积可知,
在弱解意义下是s-阶调和映射当且仅当
2. 定理1的证明
我们将证明分成以下几步:
引理2.1 我们有
证明:因为
是问题(3)的解,对任意
我们有
取
,我们得到
引理2.2 我们有
证明:因为
,我们有
,所以
引理2.3
在空间
中强收敛至
。
证明:根据引理2.1和引理2.2,我们有
从而,我们有
对这个不等式求和,设N为任意正整数,于是我们有
所以级数
收敛。
再根据Sobolev嵌入定理,
在空间
中强收敛至
。
引理2.4
在空间
中弱收敛到
且
是s-阶调和映射。
证明:根据引理2.1可知,
在空间
中有界,从而存在 使得
在空间
中弱收敛到
。因为
且
在弱拓扑意义下是
的闭子集,从而
。
使得
在空间
中弱收敛到
。因为
且
在弱拓扑意义下是
的闭子集,从而
。
下面我们证明
是s-阶调和映射。注意到
满足的欧拉–拉格朗日方程为
取
,这里
,于是我们有
进一步,我们有
取极限我们得到
这等价于
最后,令
,
且
,于是根据向量恒等式:对于任意的
,
,我们有
所以
因此,根据注记1可知
在弱解意义下是s-阶调和映射。
综上所述,定理1得证。
注记2 设
是极小值问题(3)的解,则它是唯一的。事实上,设
和
都是解,则
和
成立,于是我们有
。这意味着
。
注记3 设
是极小值问题(3)的解,则u是s-阶调和映射当且仅当
。事实上,若
,我们有
从而u是s-阶调和映射。上述过程可逆,从而充分条件成立。