一类受衰减噪声扰动的单种群模型2-周期解的渐进稳定性

doi:10.12677/AAM.2022.114222

期刊菜单

一类受衰减噪声扰动的单种群模型2-周期解的渐进稳定性
Asymptotic Stability of 2-Cycle Solutions for a Class of Single Population Models Perturbed by Attenuating Noise

DOI: 10.12677/AAM.2022.114222, PDF, HTML, XML, 下载: 368 浏览: 480
作者: 李佳倩, 廖新元^*：南华大学，数理学院，湖南衡阳
关键词: 2-周期解；衰减扰动；渐进稳定；数值模拟；2-Cycle Solution； Decaying Perturbation； Asymptotic Stability； Numerical Simulation

摘要: 本文考虑了一种受衰减噪声扰动的随机单种群模型，在一定的条件下，根据随机差分方程稳定性相关理论，讨论了该模型2-周期解的存在性及渐进稳定性，利用MATLAB进行数值仿真，验证本文所得结论的正确性。

Abstract: In this paper, a random single population model disturbed by decaying noise is considered. Under certain conditions, according to the stability theory of stochastic difference equations, the existence and asymptotic stability of the 2-cycle solution of the model are discussed. Using MATLAB, numerical simulation is carried out to verify the correctness of the conclusions obtained in this paper.

文章引用：李佳倩, 廖新元. 一类受衰减噪声扰动的单种群模型2-周期解的渐进稳定性[J]. 应用数学进展, 2022, 11(4): 2048-2054. https://doi.org/10.12677/AAM.2022.114222

1. 引言

近些年来，越来越多的人开始注意到，事物的发展都受到不同形式、不同程度外界随机干扰因素的影响。因此，在确定性模型的基础上，众多学者构建更符合实际动力学性态的随机模型进行研究，并得到了许多研究结果。例如，Beatrice-Paternoster [1] 等研究了一类分数阶随机差分方程的稳定性；Zairan Su [2] 等研究了两个随机单种群模型，得到了系统平稳分布及平衡点渐进稳定的条件；J. Appleby [3] 等研究了一类具有非双曲平衡和衰减噪声扰动的非线性差分方程的局部稳定性，Leonid-Shaikhet [4] 研究了一类连续时间和受衰减噪声扰动的随机差分方程，得到了系统稳定性的条件。更多研究结果见参考文献 [5] [6] [7] [8]。

然而，现实生活中很多实际问题都符合周期行为的特征。比如，果树收成往往以两年为周期，“大年”和“小年”轮换。一些大城市郊区的高速公路上，常见到以两星期为周期的交通堵塞。我国某些地区的生猪产量，也有两年周期的起落。对于随机差分方程周期解的稳定性研究较少 [9] [10] [11]，值得我们更进一步的研究。因此，本文基于文献 [10]，将确定性方程的循环行为与随机扰动相结合，研究了一类受衰减噪声扰动的单种群模型2-周期解的渐进稳定性。

2. 预备知识

著名的Smith提出密度制约的单种群Logistic模型 [12]

$N (t + 1) = N (t) [1 + r (1 - \frac{N (t)}{k})],$ (1)

其中r > 0为种群的自然增长率，k > 0为环境的最大容纳量。

设 $(Ω, F, P)$ 是完备概率空间，关于概率的一些概念和符号说明见文献 [13]。

本文需要下面的一些定义和引理。

定义2.1对任意的 $r \in (a, b)$ ， $F_{r} (x)$ 是 $R \to R$ 上连续可微的函数，定义：

$F_{r}^{2} (x) = F_{r} (F_{r} (x)),$ (2)

且 $F_{r}^{2} (x)$ 也是 $R \to R$ 上连续可微的函数。

定义2.2满足条件 $F_{r}^{2} (x) = x$ 且 $F_{r} (x) \neq x$ 的解称为方程 $x_{n + 1} = F_{r} (x_{n}), n \in N$ 的2-周期解。

引理2.1 [14] 假设方程

$x_{n + 1} = F_{r} (x_{n}), n \in N,$ (3)

有2-周期解： ${x_{r} (0), x_{r} (1)}$ ，当 $r \in (c, d) \subset (a, b)$ 时，满足条件

$| {(F_{r}^{2})}^{'} (x_{r} (0)) | = | {F^{'}}_{r} (x_{r} (0)) | | {F^{'}}_{r} (x_{r} (1)) | = k_{r} < 1,$ (4)

则方程的2-周期解 ${x_{r} (0), x_{r} (1)}$ 在 $r \in (c, d)$ 上是渐进稳定的。

在本文中，含有参数的差分方程受衰减的随机噪声扰动，即

当 $n \to \infty$ 时， $ρ_{n} \to 0$ 。 (5)

引理2.2 [15] 当 $n \to \infty$ 时， $ρ_{n} \to 0$ 几乎确定，则对任意 $γ \in (0, 1)$ ，存在 $Ω_{γ} \subseteq Ω$ ， $j (γ)$ 满足：

$\sup_{n \in N} | ρ_{t} (ω) | < j (γ), ω \in Ω_{γ}, P (Ω_{γ}) > 1 - γ .$ (6)

引理2.3设 $k_{1} \in (0, 1), α_{i} \geq 0$ ，对每个 $i \in N$ 且 $\lim_{i \to \infty} α_{i} = 0$ ，则当 $n \to \infty$ 时， $\sum_{i = 0}^{n} k_{1}^{i} α_{n - i} \to 0$ 。

证明： $\forall ε_{0} > 0$ ，存在 $N_{1} \in N$ 时，满足 $\frac{α_{i} k_{1}^{N_{1} + 1}}{1 - k_{1}} < \frac{ε_{0}}{2}$ 。

由 $\lim_{i \to \infty} α_{i} = 0$ 可得，存在 $N_{2} \in N$ ，当 $n \geq N_{2}$ 时，有 $α_{n} < \frac{ε_{0} (1 - k_{1})}{2}$ 。

那么，当 $n > N_{1} + N_{2}$ 时，有

$\begin{matrix} \sum_{i = 0}^{n} k_{1}^{i} α_{n - i} = \sum_{i = 0}^{N_{1}} k_{1}^{i} α_{n - i} + \sum_{i = N_{1} + 1}^{n} k_{1}^{i} α_{n - i} \\ \leq \max_{j \geq N_{2}} {α_{j}} \sum_{i = 0}^{N_{1}} k_{1}^{i} + β k_{1}^{N_{1} + 1} \sum_{i = 0}^{\infty} k_{1}^{i} \\ \leq \frac{ε_{0} (1 - k_{1})}{2} \frac{1}{1 - k_{1}} + α k_{1}^{N_{1} + 1} \frac{1}{1 - k_{1}} < ε_{0} . \end{matrix}$ (7)

所以，当 $n \to \infty$ 时， $\sum_{i = 0}^{n} k_{1}^{i} α_{n - i} \to 0$ 。

引理2.4 [16] 方程 $F_{r} (x) = x [1 + r (1 - \frac{x}{k})]$ 有 $x_{1} = 0, x_{2} = k$ 两个平衡点。当 $r \in (0, 2)$ 时，有稳定的平衡点；当 $r \in (2, 2.449)$ 时，有稳定的2-周期解；当 $r \in (2.449, 2.544)$ 时，有稳定的4-周期解；当 $r \in (2.544, 2.570)$ 时，出现倍周期分岔现象；当r大于2.570时，出现混沌现象。

3. 二周期解的渐进稳定性

本文根据Smith的密度制约单种群模型，提出下列离散模型：

$X_{n + 1} = X_{n} [1 + r (1 - \frac{X_{n}}{k})] + ε σ_{n} ξ_{n + 1}, n \in N$ (8)

其中， $σ_{n} = {(n + 1)}^{- 0.5}$ 是一个非随机非负系数序列， $ξ_{n} ~ N (0, 1)$ 是随机变量， $ε > 0$ 是一个常数， $r \in (c, d) > 0$ 。

定理3.1对 $r \in (c, d)$ ， $γ \in (0, 1)$ ， $ω \in Ω_{γ}$ ，任取 $ε_{0} (r, γ) > 0$ ，存在 $δ_{1} (r) > 0$ ， $P (Ω_{γ}) > 1 - γ$ ， $Ω_{γ} \subseteq Ω$ ，当 $ε < ε_{0}$ 时，方程(8)有唯一的初值 $X_{0} \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1})$ ，则其解 $X_{n} (ω)$ 满足

$X_{2 k} (ω) \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1}), k \in N$ (9)

且

$\lim_{k \to \infty} X_{2 k} = x_{r} (0), \lim_{k \to \infty} X_{2 k + 1} = x_{r} (1) .$ (10)

即方程(8)存在渐进稳定的2-周期解。

证明：令 $F_{r} (X_{n}) = X_{n} [1 + r (1 - \frac{X_{n}}{k})]$ ， $ρ_{n} = σ_{n - 1} ξ_{n}, n \in N$ ， $ρ_{n}$ 是满足条件(5)的随机变量，则方程(8)可变为

$X_{n + 1} = F_{r} (X_{n}) + ε ρ_{n + 1}, n \in N$ (11)

对连续可微的函数 $F_{r}^{2} (x), r \in (\bar{r}, \hat{r})$ ，存在 $δ_{1} \in (0, 1), k_{1} \in (k_{r}, 1)$ ，且 $x \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1})$ ，使得

$| (F_{r}^{2})' (x) | < k_{1} < 1.$ (12)

设 $0 < β < 1$ ， $| β_{1} | \leq | β |$ ， $| β_{2} | \leq | β |$ ， $ζ$ 介于 $F_{r} (x)$ 和 $F_{r} (x) + β_{1}$ 之间，由罗尔中值定理可得

$F_{r} (F_{r} (x) + β_{1}) - F_{r} (F_{r} (x)) = {F^{'}}_{r} (ζ) β_{1}$ (13)

由 $F_{r}^{2} (x) = F_{r} (F_{r} (x))$ 可得：

$F_{r} (F_{r} (x) + β_{1}) + β_{2} - F_{r}^{2} (x) = {F^{'}}_{r} (ζ) β_{1} + β_{2}$ (14)

令 $T_{r}^{(1)} = \min_{x \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1})} {F_{r} (x)}, T_{r}^{(2)} = \max_{x \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1})} {F_{r} (x)}, T_{r}^{(3)} = \max_{x \in (T_{r}^{(1)} - 1, T_{r}^{(1)} + 1)} {{F^{'}}_{r} (x)}$ ，则

$| F_{r} (F_{r} (x) + β_{1}) + β_{2} - F_{r}^{2} (x) | \leq | {F^{'}}_{r} (ζ) | | β_{1} | + | β_{2} | \leq | β | [T_{r}^{(3)} + 1] .$ (15)

因为 ${x_{r} (0), x_{r} (1)}$ 是方程的2-周期解，则 $F_{r}^{2} (x_{r} (0)) = x_{r} (0)$ 。

因此，当 $x_{0} \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1})$ 时，有：

$\begin{matrix} | F_{r} (F_{r} (x) + β_{1}) + β_{2} - x_{r} (0) | = | F_{r} (F_{r} (x) + β_{1}) + β_{2} - F_{r}^{2} (x_{r} (0)) | \\ \leq | F_{r} (F_{r} (x) + β_{1}) + β_{2} - F_{r}^{2} (x_{0}) | + | F_{r}^{2} (x_{r} (0)) - F_{r}^{2} (x_{0}) | \\ \leq | β | [T_{r}^{(3)} + 1] + k_{1} | x_{r} (0) - x_{0} | \\ \leq | β | [T_{r}^{(3)} + 1] + k_{1} δ_{1} \end{matrix}$ (16)

接下来，令 $| β | [T_{r}^{(3)} + 1] + k_{1} δ_{1} < δ_{1}$ ，则

$| β | < \frac{δ_{1} (1 - k_{1})}{T_{r}^{(3)} + 1}$ (17)

根据引理2.1，令 $β_{1} = ε ρ_{1} (ω), β_{2} = ε ρ_{2} (ω), ω \in Ω_{γ}$ ，则

$ε < \frac{δ_{1} (1 - k_{1})}{[T_{r}^{3} + 1] j (γ)} .$ (18)

根据(16)得

$\begin{matrix} | X_{2} (ω) - x_{r} (0) | = | F_{r} (F_{r} (X_{0} (ω) + ε ρ_{1} (ω))) + ε ρ_{2} (ω) - x_{r} (0) | \\ = | F_{r} (F_{r} (X_{0} (ω) + θ_{1})) + θ_{2} - x_{r} (0) | < δ_{1} \end{matrix}$ (19)

因此 $X_{2} (ω) \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1})$ 。

由递推法可得 $X_{2 k} (ω) \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1}), k \in N$ 。

当 $ω \in Ω_{γ}$ ， $x \in (x_{r} (0) - δ_{1}, x_{r} (0) + δ_{1})$ ， $| β_{1} |, | β_{2} | < 1$ ， $n \in N$ 时，令

$ϑ (x, β_{1}, β_{2}) : = F_{r} (F_{r} (x) + β_{1}) + β_{2} - F_{r}^{2} (x), ϑ (n, ω) : = ϑ (X_{2 n} (ω), ε ρ_{2 n + 1} (ω), ε ρ_{2 (n + 1)} ( ω ))$

由(15)可得

$| ϑ (n, ω) | \leq T_{r}^{(3)} | ε ρ_{2 n + 1} (ω) | + ε | ρ_{2 (n + 1)} (ω) | : = α_{2 n}$ (20)

对任意 $ω \in Ω_{γ}$ ， $n \in N$ ，存在一些 $α > 0$ ，当 $n \to \infty$ 时， $α_{2 n} < α$ ， $α_{2 n} \to 0$ 。

令 $Δ_{n} (ω) = | X_{2 n} (ω) - x_{r} (0) |$ 。

根据 $x_{r} (0) = F_{r}^{2} (x_{r} (0))$ 可得

$\begin{matrix} Δ_{n + 1} (ω) = | X_{2 (n + 1)} (ω) - x_{r} (0) | \\ = | F_{r}^{2} (X_{2 n} (ω)) - F_{r}^{2} (x_{r} (0)) + ϑ (n, ω) | \\ \leq | F_{r}^{2} (X_{2 n} (ω)) - F_{r}^{2} (x_{r} (0)) | + | ϑ (n, ω) | \\ \leq k_{1} | X_{2 n} (ω) - x_{r} (0) | + α_{2 n} \\ = k_{1} Δ_{n} (ω) + α_{2 n} \end{matrix}$ (21)

通过递推法可得

$Δ_{n + 1} (ω) \leq k_{1}^{n + 1} | x_{0} - x_{r} (0) | + \sum_{i = 0}^{n} k_{1}^{i} α_{2 (n - i)}$ (22)

由引理2.2可得，当 $ω \in Ω_{γ}, n \to \infty$ 时， $X_{2 n} (ω) \to x_{r} (0)$ 。

同理可证，当 $ω \in Ω_{γ}, n \to \infty$ 时， $X_{2 n + 1} (ω) = F_{r} (X_{2 n} (ω)) + ρ_{2 n + 1} \to F_{r} (x_{r} (0)) = x_{r} (1)$ 。

即方程(8)存在渐进稳定的2-周期解。

4. 数值模拟

方程(8)的2-周期解 ${x_{r} (0), x_{r} (1)}$ 为：

$x_{r} (0) = \frac{k (r + 2)}{2 r} + \frac{k}{2 r} \sqrt{(r + 2) (r - 2)}, x_{r} (1) = \frac{k (r + 2)}{2 r} - \frac{k}{2 r} \sqrt{(r + 2) (r - 2)}$

由引理2.4得，令 $r = 2.2, k = 1$ ，得到 $x_{2.2} (0) \approx 0.746$ 。

令 $δ_{1} = 0.001$ ，则

$\begin{matrix} \max_{x \in [0.745, 0.747]} | (F_{r}^{2})' (x) | = \max_{x \in [0.745, 0.747]} | {(1 + r)}^{2} - \frac{2 (r^{3} + 3 r^{2} + 2 r)}{k} x + \frac{3 (2 r^{2} + 2 r^{3})}{k} x^{2} - \frac{4 r^{3}}{k^{3}} x^{3} | \\ = | \max_{x \in [0.745, 0.747]} {(1 + r)}^{2} + \frac{3 (2 r^{2} + 2 r^{3})}{k} x^{2} - \min_{x \in [0.745, 0.747]} \frac{2 (r^{3} + 3 r^{2} + 2 r)}{k} x + \frac{4 r^{3}}{k^{3}} x^{3} | \\ = | {(1 + r)}^{2} + \frac{3 (2 r^{2} + 2 r^{3})}{k} \times {0.747}^{2} - \frac{2 (r^{3} + 3 r^{2} + 2 r)}{k} \times 0.745 - \frac{4 r^{3}}{k^{3}} \times {0.745}^{3} | \\ \approx 0.4268 < 0.43 \end{matrix}$

因此， $k_{1} = 0.43$ 。

$\begin{array}{l} T_{r}^{(1)} = \min_{x \in (0.745, 0.747)} {x [1 + r (1 - \frac{x}{k})]} = 1.1627802 \\ T_{r}^{(2)} = \max_{x \in (0.745, 0.747)} {x [1 + r (1 - \frac{x}{k})]} = 1.162945 \\ T_{r}^{(3)} = \max_{x \in (0.1627802, 2.162945)} {{F^{'}}_{r} (x)} \approx 2.4838 \end{array}$

由文献 [10] 得 $j (γ) = \sqrt{2}$ 。

由(18)得：

$ε < \frac{δ_{1} (1 - k_{1})}{[T_{r}^{3} + 1] j (γ)} = \frac{0.001 \times (1 - 0.43)}{(2.4838 + 1) \times \sqrt{2}} \approx 0.000116.$

通过数值仿真得到方程的二周期解的稳定性图像如图1，为了作出对比，也得到了当 $ε = 0.1$ 时方程解的图像，如图2。由此可知， $ε$ 的理论计算值影响2-周期解的稳定性。

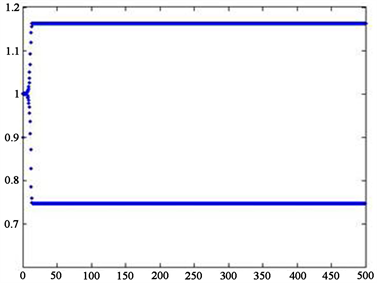
Figure 1. $r = 2.2, ε = 0.000116$

图1. $r = 2.2, ε = 0.000116$

Figure 2. $r = 2.2, ε = 0.1$

图2. $r = 2.2, ε = 0.1$

5. 结论

本文考虑了一种受衰减噪声扰动的随机单种群模型。对于该模型，根据方程二周期解渐进稳定性定理，证明该随机差分方程2-周期解是渐进稳定的，结果表明，在衰减噪声扰动下系统的稳定性保持不变，并通过MATLAB数值仿真充分验证了结果。

NOTES

^*通讯作者。

参考文献

[1]	Paternoster, B. and Shaikhet, L. (2008) Stability of Equilibrium Points of Fractional Difference Equations with Stochastic Perturbations. Advances in Difference Equations, 2008, Article No. 718408. https://doi.org/10.1155/2008/718408
[2]	Sun, Z.R., Lv, J.L. and Zou, X.L. (2020) Dynamical Analysis on Two Stochastic Single-Species Models. Applied Mathematics Letters, 99, Article ID: 105982. https://doi.org/10.1016/j.aml.2019.07.013
[3]	Appleby, J., Berkolaiko, G. and Rodkina, A. (2008) On Local Stability for a Nonlinear Difference Equation with a Non-Hyperbolic Equilibrium and Fading Stochastic Perturbations. Journal of Difference Equations and Applications, 14, 923-951. https://doi.org/10.1080/10236190701871786
[4]	Shaikhet, L. (2019) About Stability of Difference Equations with Continuous Time and Fading Stochastic Perturbations. Applied Mathematics Letters, 98, 284-291. https://doi.org/10.1016/j.aml.2019.06.029
[5]	Palmer, P. (2012) Application of a Discrete Itô Formula to Determine Stability (Instability) of the Equilibrium of a Scalar Linear Stochastic Difference Equation. Computers & Mathematics with Applications, 64, 2302-2311. https://doi.org/10.1016/j.camwa.2012.03.012
[6]	Shaikhet, L. (2015) Stability of Equilibrium States for a Stochastically Perturbed Exponential Type System of Difference Equations. Journal of Computational and Applied Mathematics, 290, 92-103. https://doi.org/10.1016/j.cam.2015.05.002
[7]	Smítal, J. and Steele, T.H. (2009) Stability of Dynamical Structures under Perturbation of the Generating Function. Journal of Difference Equations and Applications, 15, 77-86. https://doi.org/10.1080/10236190802563761
[8]	Berkolaiko, G. and Rodkina, A. (2006) Almost Sure Convergence of Solutions to Non-Homogeneous Stochastic Difference Equation. Journal of Difference Equations and Applications, 12, 535-553. https://doi.org/10.1080/10236190600574093
[9]	邓小炎. 一类单种群差分模型的周期解和混沌现象[J]. 华中农业大学学报, 2000, 19(4): 403-407. https://doi.org/10.13300/j.cnki.hnlkxb.2000.04.027
[10]	Braverman, E. and Rodkina, A. (2012) On Difference Equations with Asymptotically Stable 2-Cycles Perturbed by a Decaying Noise. Computers & Mathematics with Applications, 64, 2224-2232. https://doi.org/10.1016/j.camwa.2012.01.057
[11]	Braverman, E. and Rodkina, A. (2013) Stabilization of Two Cycles of Difference Equations with Stochastic Perturbations. Journal of Difference Equations and Applications, 19, 1192-1212. https://doi.org/10.1080/10236198.2012.726989
[12]	李石涛, 李冬梅, 曲国坤. 一类具有收获的离散单种群模型稳定性与混沌[J]. 哈尔滨理工大学学报, 2006, 11(6): 78-80.
[13]	Shiryaev, A.N. (1996) Probability. 2nd Edition, Springer, Berlin. https://doi.org/10.1007/978-1-4757-2539-1
[14]	Elaydi, S. (2005) An Introduction to Difference Equations. 3rd Edition, Springer, Berlin.
[15]	Appleby, J.A.D., Kelly, C., Mao, X., et al. (2010) On the Local Dynamics of Polynomial Difference Equations with Fading Stochastic Perturbations. Dynamics of Continuous Discrete and Impulsive Systems Series A: Mathematical Analysis, 17, 401-430.
[16]	陈兰荪. 数学生态学模型与研究方法[M]. 北京: 科学出版社, 1988.

为你推荐

友情链接