浅谈高等数学在高中数学教材中的渗透——以人教A版为例

A Brief Talk on the Infiltration of Advanced Mathematics in Senior High School Mathematics Textbooks—Taking the People’s Education Version A as an Example

摘要: 学生学习知识是一个连贯的过程，做好小学与初中、初中与高中、高中与大学的衔接至关重要。高中数学知识与大学数学知识联系密切，教材习题的编制、高考试题的命制常会以高等数学作为背景。本文例析函数的凹凸性、重要极限、泰勒公式、直线的点向式方程与平面的点法式方程在高中数学教材中的渗透，并由此得到一些教学启示。

Abstract: Students’ learning knowledge is a coherent process. It is very important to do a good job in the connection between primary school and junior high school, junior high school and senior high school, senior high school and university. The knowledge of high school mathematics is closely related to the knowledge of college mathematics. The compilation of textbook exercises and the formulation of college entrance examination questions often take higher mathematics as the background. This paper analyzes the penetration of concavity and convexity of function, important limit , Taylor formula, pointwise equation of straight line and point normal equation of plane in senior high school mathematics textbooks, and obtains some teaching enlightenment.

1. 引言

菲利克斯•克莱因指出：基础数学的教师应该站在更高的视角(高等数学)来审视、理解初等数学问题，只有观点高了，事物才能显得明了而简单 [1] 。正所谓“站得高，看得远”，利用高等数学的知识、思想和方法分析问题，能让我们在问题解决时实现突破和飞跃。近年来，基于高观点视角进行初等数学的教学研究已成为一大热点问题。此外，现阶段教育越来越注重创造型人才的培养，越来越注重学生创新思维能力的培养，高考数学试题也越来越注重创新，“题海战术”已然不能“应对”高考，学生创新思维能力的培养迫在眉睫。教材作为教学的第一手资源，从章前言、正文、旁白、例题、习题到拓展阅读都经过了无数的科学考量和验证，回归教材才能“治标治本”，从教材出发，探析高等数学在高中数学中的渗透是很有必要的。

2. 渗透例析

2.1. 函数的凹凸性

凸函数与凹函数的定义 [2] ：设f为定义在区间I上的函数，若对I上的任意两点 $x_1,x_2$ 和任意实数 $\lambda \in \left(0,1\right)$ 总有 $f\left(\lambda x_1+\left(1-\lambda \right)x_2\right)\le \lambda f\left(x_1\right)+\left(1-\lambda \right)f(x_2)$ ，则称f为I上的凸函数。反之，如果总有 $f\left(\lambda x_1+\left(1-\lambda \right)x_2\right)\ge \lambda f\left(x_1\right)+\left(1-\lambda \right)f\left(x_2\right)$ ，则称f为I上的凹函数。几何形状如图1、图2所示(其中 $x=\lambda x_1+\left(1-\lambda \right)x_2$ ， $C=\lambda f\left(x_1\right)+\left(1-\lambda \right)f\left(x_2\right)$ )。

人教A版普通高中数学教科书函数的概念与性质章节复习参考题呈现了以函数的凹凸性为背景的证明题如下：“证明：(1) 若 $f\left(x\right)=ax+b$ ，则 $f\left(\frac{x_1+x_2}{2}\right)=\frac{f\left(x_1\right)+f\left(x_2\right)}{2}$ ；(2) 若 $g\left(x\right)=x^2+ax+b$ ，则 $g\left(\frac{x_1+x_2}{2}\right)\le \frac{g\left(x_1\right)+g\left(x_2\right)}{2}$ 。” [3] 。该习题正是函数的凹凸性定义中当 $\lambda =\frac{1}{2}$ 时的特殊情形，所需证明结果呈现了：(1) 一次函数(a ≠ 0时)或常数函数(a = 0时)中点值等于端点值的平均值；(2) 开口向上二次函数为凸函数，中点值小于等于端点值的平均值( $x_1=x_2$ 时取等号)，考查学生利用函数解析式求值，把 $x_1$ 、 $x_2$ 、 $\frac{x_1+x_2}{2}$ 代入函数解析式化简再进行比较即可。对于

Figure 1. Schematic diagram of convex function

图1. 凸函数示意图

Figure 2. Schematic diagram of concave function

图2. 凹函数示意图

$f\left(x\right)=ax+b$ ， $f\left(\frac{x_1+x_2}{2}\right)=\frac{a\left(x_1+x_2\right)}{2}+b$ ， $\frac{f\left(x_1\right)+f\left(x_2\right)}{2}=\frac{\left(a{x}_1+b\right)+\left(a{x}_2+b\right)}{2}=\frac{a\left(x_1+x_2\right)}{2}+b$ ，从而 $f\left(\frac{x_1+x_2}{2}\right)=\frac{f\left(x_1\right)+f\left(x_2\right)}{2}$ 。对于 $g\left(x\right)=x^2+ax+b$ ， $g\left(\frac{x_1+x_2}{2}\right)={\left(\frac{x_1+x_2}{2}\right)}^2+a\left(\frac{x_1+x_2}{2}\right)+b$ ， $\frac{g\left(x_1\right)+g\left(x_2\right)}{2}=\frac{\left(x_1^2+a{x}_1+b\right)+\left(x_2^2+a{x}_2+b\right)}{2}=\frac{x_1^2+x_2^2}{2}+a\left(\frac{x_1+x_2}{2}\right)+b$ ，由基本不等式知 ${\left(\frac{x_1+x_2}{2}\right)}^2\le \frac{x_1^2+x_2^2}{2}$ ，从而 $g\left(\frac{x_1+x_2}{2}\right)\le \frac{g\left(x_1\right)+g\left(x_2\right)}{2}$ 。该题以高等数学中函数的凹凸性为背景进行命题，渗透数形结合的思想方法，考查学生的运算求解能力和直观想象能力，教师在习题讲解时若进行拓展，让学生掌握几何直观模型，学生将能从直观上感知结果(如图3、图4)。若对该题进行延伸和推广，即能得到著名的不等式：琴生不等式。

Figure 3. Visual model of Question (1)

图3. 第(1)问的直观模型图

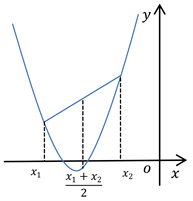
Figure 4. Visual model of Question (2)

图4. 第(2)问的直观模型图

2.2. 重要极限 $\underset{x\to \infty }{lim}{\left(1+\frac{1}{x}\right)}^x=e$

高等数学内容涉及两个重要极限，其一为 $\underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=\text{e}$ [2] 。人教A版普通高中数学教科书指数函数与对数函数章节习题4.1呈现了以重要极限 $\underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=\text{e}$ 为背景的习题如下：“(1) 当 $n=1,2,3,10,100,1000,10000,100000,\cdots$ 时，用计算工具计算 ${\left(1+\frac{1}{n}\right)}^n\left(n\in N^{*}\right)$ 的值；(2) 当n越来越大时， ${\left(1+\frac{1}{n}\right)}^n$ 的底数越来越小，而指数越来越大，那么 ${\left(1+\frac{1}{n}\right)}^n$ 是否也会越来越大？有没有最大值？” [3] 。该习题正是重要极限 $\underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=\text{e}$ 当 $x\in N^{*}$ 时的特殊情形，利用计算工具逐次进行计算或借助信息技术软件，如GeoGebra软件进行探究(如图5，设置滑动条 $n\in N^{*}$ ，在指令框中输入 $a={\left(1+\frac{1}{n}\right)}^n$ ，拖动滑动条)。可发现当n无限大时， ${\left(1+\frac{1}{n}\right)}^n$ 无限趋近于e，但没有最大值。该题涉及指数幂的运算，对于高中阶段的学生来说，要得出结果，需要借助计算工具。教师在讲解该题时，若能进行补充，给出该重要极限，学生将能快速得出第(2)问的答案，且对后续导数部分的学习也能提供很大的帮助，如对数函数 $y=f(x)={\log }_{a}x$ (a > 0，且a ≠ 1)的导数的推导：

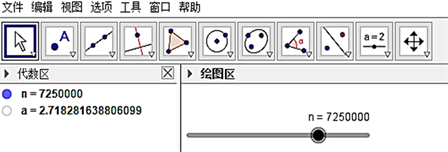
Figure 5. Process diagram of using GeoGebra software to explore whether ${\left(1+\frac{1}{n}\right)}^n$ will become larger and larger

图5. 利用GeoGebra软件探究 ${\left(1+\frac{1}{n}\right)}^n$ 是否会越来越大的过程图

$\frac{\Delta y}{\Delta x}=\frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}=\frac{{\log }_a\left(x+\Delta x\right)-{\log }_{a}x}{\Delta x}=\frac{1}{\Delta x}{\log }_a\frac{x+\Delta x}{x}=\frac{1}{\Delta x}{\log }_a\left(1+\frac{\Delta x}{x}\right)$

$={\log }_a{\left(1+\frac{\Delta x}{x}\right)}^{\frac{1}{\Delta x}}={\log }_a{\left(1+\frac{1}{\frac{x}{\Delta x}}\right)}^{\frac{1}{\Delta x}}=\frac{1}{x}{\log }_a{\left(1+\frac{1}{\frac{x}{\Delta x}}\right)}^{\frac{x}{\Delta x}}$ ， $\underset{\frac{x}{\Delta x}\to \infty }{\lim }{\left(1+\frac{1}{\frac{x}{\Delta x}}\right)}^{\frac{x}{\Delta x}}=\text{e}$ ， $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{1}{x}{\log }_a{\left(1+\frac{1}{\frac{x}{\Delta x}}\right)}^{\frac{x}{\Delta x}}=\frac{1}{x}{\log }_a\text{e}=\frac{1}{x\ln a}$ ，所以 $y^{\prime }=\frac{1}{x\ln a}$ 。

2.3. 泰勒公式

高等数学内容涉及带有佩亚诺余项的麦克劳林公式(泰勒公式的特殊形式)： $f\left(x\right)=f\left(0\right)+f^{\prime }\left(0\right)x+\frac{f^{″}\left(0\right)}{2!}{x}^2+\cdots +\frac{f^{\left(n\right)}\left(0\right)}{n!}{x}^n+o\left(x^n\right)$ [2] 。人教A版普通高中数学教科书三角函数章节复习参考题呈现了以泰勒公式为背景的习题如下：“英国数学家泰勒发现了如下公式： $\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$ ， $\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots$ ，其中 $n!=1\times 2\times 3\times 4\times \cdots \times n$ 。这些公式被编入计算工具，计算工具计算足够多的项就可以确保显示值的精确性。比如，用前三项计算 $\cos 0.3$ ，就得到 $\cos 0.3\approx 1-\frac{{0.3}^2}{2!}+\frac{{0.3}^4}{4!}=0.9553375$ 。试用你的计算工具计算 $\cos 0.3$ ，并与上述结果比较。” [3] 。该习题正是函数 $y=\sin x$ 与函数 $y=\cos x$ 的麦克劳林公式。在高中导数的解题过程中，常用到一些不等式的结论，如 ${\text{e}}^x\ge 1+x$ ，此不等式的结果可从函数 $y={\text{e}}^x$ 的麦克劳林公式 ${\text{e}}^x=1+x+\frac{x^2}{2!}+\cdots +\frac{x^n}{n!}+o\left(x^n\right)$ 直接得出。该题让学生感知“非特殊”三角函数值的估计与计算，渗透高等数学中的泰勒公式。掌握常用函数 $y=\sin x$ ， $y=\cos x$ ， $y={\text{e}}^x$ 的麦克劳林公式，在解题时能起到很大的便利作用，教师在教学时可根据学情适时适当进行渗透。

2.4. 直线的点向式方程与平面的点法式方程

人教A版普通高中数学教科书空间向量与立体几何章节习题1.4呈现了直线的点向式方程与平面的点法式方程证明题如下：“在空间直角坐标系中，已知向量 $u=\left(a,b,c\right)\left(abc\ne 0\right)$ ，点 $P_0\left(x_0,y_0,z_0\right)$ ，点 $P\left(x,y,z\right)$ 。(1) 若直线l经过点 $P_0$ ，且以 $u$ 为方向向量，P是直线l上的任意一点，求证： $\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$ ；(2) 若平面 $\alpha$ 经过点 $P_0$ ，且以 $u$ 为法向量，P是平面 $\alpha$ 内的任意一点，求证： $a\left(x-x_0\right)+b\left(y-y_0\right)+c\left(z-z_0\right)=0$ 。” [4] 。该习题所需证明结果恰为直线的点向式方程与平面的点法式方程，该结果让学生充分体会一条直线由一定点和其方向向量确定，一个平面由一定点和其法向量确定，渗透数形结合的思想方法。知道了直线的点向式方程与平面的点法式方程，学生在遇到方程表达式时也能判别是否为直线或者平面。该题证明过程如下：

如图6，因为 $u$ 为直线l的方向向量，所以 $\stackrel{\to }{P_{0}P}=\lambda u$ ，即 $\left(x-x_0,y-y_0,z-z_0\right)=\lambda \left(a,b,c\right)=\left(\lambda a,\lambda b,\lambda c\right)$ ，则 $\{\begin{array}{l}x-x_0=\lambda a\\ y-y_0=\lambda b\\ z-z_0=\lambda c\end{array}$ ，从而 $\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$ 。如图7，因为 $u$ 为平面 $\alpha$ 的法向量，所以 $\stackrel{\to }{P_{0}P}\cdot u=0$ ，即 $\left(x-x_0,y-y_0,z-z_0\right)\cdot \left(a,b,c\right)=0$ ，从而 $a\left(x-x_0\right)+b\left(y-y_0\right)+c\left(z-z_0\right)=0$ 。直线的点向式方程与平面的点法式方程在高中阶段未直接讲授，但在高等数学内容中有所涉及，该习题呈现该结果，也充分体现了高中数学与大学数学的衔接。

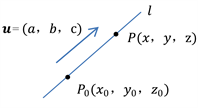
Figure 6. Schematic diagram of point-direction equation analysis of straight line

图6. 直线的点向式方程分析示意图

Figure 7. Schematic diagram of plane point method equation analysis

图7. 平面的点法式方程分析示意图

3. 教学启示

本文分析了函数的凹凸性、重要极限 $\underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=\text{e}$ 、泰勒公式、直线的点向式方程与平面的点法式方程在高中数学教材中的渗透，让我们看到高中数学与大学数学的联系。高等数学在高中数学教材中渗透，一方面让学生初步接触高等数学的内容，体会“高观点”下的数学思想和方法，一方面启示高中数学教师应做好高中与大学的衔接，拓展学生的知识视域，引导学生从更高的视角思考和分析问题。学生“居高临下”的学习，是主动接受信息和创造性思维的产生过程 [5] 。除教材正文所渗透的高等数学内容外，很多高等数学背景下的知识，若教师在教学过程中适时适当进行渗透、推广、拓展，能帮助学生快速解题，如极限、洛必达法则、拉格朗日中值定理、极值的充分条件等，在导数综合大题的解决中能起到很大的作用。然而需要注意的是高等数学的渗透并不是给高中数学教学增加难度和任务，而是希望广大教师从高等数学的视角出发进行教学设计及教授，用高等数学的知识、思想、方法指导高中数学课程的教学，让学生“知其然，又知其所以然”，更深刻地理解数学知识，日积月累，达到思考问题和解决问题的新高度，给学生未来的大学学习也奠定一定的基础。

高等数学进入高中数学课堂，给教师带来了新的挑战。教师应加强专业知识的学习，多看大学数学教材，如《数学分析》、《高等代数》、《解析几何》、《高等数学》等，提升自身专业素养，从高等数学的视角去解读高中数学教材。贯彻落实课标的相关要求，紧跟高考数学命题的方向，探寻初等数学与高等数学的联系，根据学情编制以高等数学为背景的练习题，锻炼学生的思维，转变“唯知识”的教学观念。注重数学思想方法的渗透，指导学生阅读可接受范畴的高等数学类课外书籍，注重校本课程的开发，给学生提供拓展性素材资源，多开展数学竞赛活动。教学之路漫漫，只有不断创新，不断进步，才能追赶时代的步伐。教师应当树立终身学习的理念，创造性教学，关注学生的长远发展，培养学生发现和提出问题的能力、分析和解决问题的能力 [6] 。

参考文献