摘要:
本文通过构造合适Lyapunov-Krasovskii泛函,采用变互式凸组合方法、自由权矩阵方法、随机分析技巧、线性矩阵不等式(LMI)方法,研究了一类随机Hopfield神经网络的随机一致最终有界性、随机吸引子的存在性以及均方指数的稳定性。我们得到了随机Hopfield神经网络的新的结果和时滞依靠的充分条件。最后,应用MATLAB数值模拟检验来得到了理论的有效性。
Abstract:
In this paper, the
problems of stochastic uniformly ultimate boundedness, the existence of stochastic
attractor and mean square exponential stability for stochastic Hopfield neural
networks are studied by constructing proper Lyapunov-Krasovskii functional,
utilizing the reciprocally con- vex approach, the free-weighting matrix method,
some stochastic analysis techniques and linear matrix inequalities technique (LMI). We deduce novel results and
delay-dependent sufficient conditions for stochastic Hopfield neural
networks. Finally, numerical simulations are given on MATLAB to verify the
effectiveness of the gained results.
1. 引言
人工神经网络是一种模仿生物神经网络的结构和功能的数学模型或计算模型,是一个普遍存在的非线性系统。近年来,由于其良好的信息处理能力和非线性映射能力,被广泛的应用到模式识别、图像处理、语音处理、DNA片段选择、数据挖掘、自动目标识别和优化等各个领域,并取得了令人瞩目的成果[1] -[3] 。自从1982年,Hopfield第一次提出了Hopfiele神经网络并且用LC电子电路进行了模拟,与此同时与Hopfield神经网络有关的动力学行为得到了学者们的广泛关注。
由于时滞在工程和现实生活中不可避免,因此研究时滞Hopfield神经网络具有一定的学术价值和实际应用。通常神经网络的很多应用都建立在神经网络的动力学行为上,包括稳定性、有界性、吸引子的存在性、周期解、收敛性、同步、混沌等[4] [5] 。我们知道当非线性系统有一个平衡点的时候研究是相对容易的,但是如果神经网络的激活函数无界可能没有平衡点或者有多个平衡点时,研究系统的平衡点的稳定性将比较困难。虽然在[6] 中,作者利用Lasalle不变理论研究了细胞神经网络的随机一致有界,而一致最终有界性和吸引子的存在性作为动态系统的一种基本性质,值得我们研究。因此在本文中,我们利用变互式凸组合的方法研究了随机Hopfield神经网络的随机一致最终有界性和随机吸引子的存在性、以及特殊情况下的均方指数稳定性。
2. 模型建立与解决
随机Hopfield神经网络描述为下面的非线性积分型微分方程:
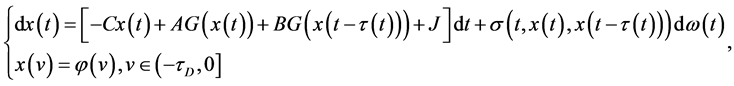 (1)
(1)
其中,连接权矩阵A,B,C为适当维数的已知常数矩阵, 是神经元的状态函数:
是神经元的状态函数: 是神经元的激励函数向量,
是神经元的激励函数向量,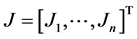 是神经网络的常值外部输入,
是神经网络的常值外部输入,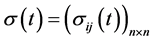 是噪声强度矩阵,
是噪声强度矩阵,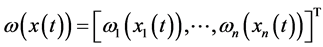 是定义在由
是定义在由 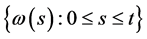 形成的自然流
形成的自然流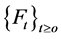 的完备空间
的完备空间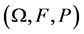 上的n维布朗运动,并且满足
上的n维布朗运动,并且满足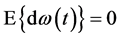 ,
,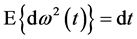 . 时变时滞
. 时变时滞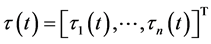 是有界的,且满足:
是有界的,且满足: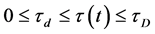 . 对于系统的初始条件
. 对于系统的初始条件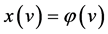 ,
, ,初始值函数为
,初始值函数为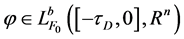 ,其中
,其中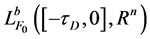 表示定义在
表示定义在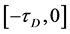 上取值于
上取值于 的随机过程
的随机过程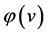 的全体,并且
的全体,并且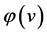 是
是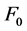 可测的,满足
可测的,满足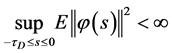 ,E定义为概率
,E定义为概率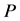 的期望.
的期望.
假设2.1:对任意的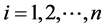 ,存在常值标量
,存在常值标量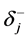 和
和 ,使得激励函数
,使得激励函数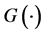 满足
满足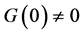 及
及
 (2)
(2)
记
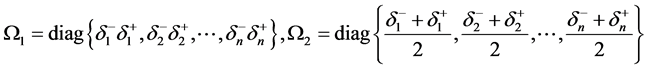 .
.
假设2.2:若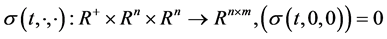 满足Lipschtiz条件,并且存在适当维数的任意矩阵
满足Lipschtiz条件,并且存在适当维数的任意矩阵 ,使得
,使得
 (3)
(3)
定义2.3 [7] :系统(1)是随机一致最终有界的,如果对任意的 ,有
,有 ,存在常值
,存在常值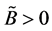 ,当
,当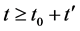 ,
,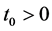 ,
,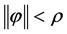 ,系统(1)的解
,系统(1)的解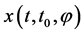 满足
满足
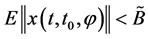 其中,
其中,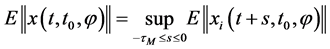 ,
, 。
。
定义2.4 [6] :非空闭集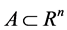 ,
,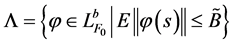 称为系统(1)的解
称为系统(1)的解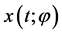 的随机吸引子,使得
的随机吸引子,使得
 其中
其中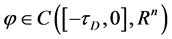
引理2.5 [8] :若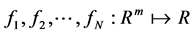 是开集
是开集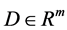 中的正值,则开集D中的变互式凸组合
中的正值,则开集D中的变互式凸组合 满足:
满足:
 , (4)
, (4)
从而有
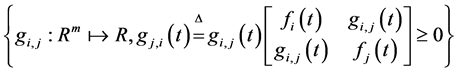 . (5)
. (5)
定理2.6:对于常值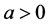 ,如果存在正定矩阵
,如果存在正定矩阵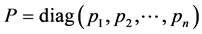 ,
,
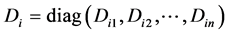 ,
,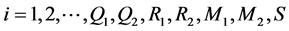 ,使得下面的线性矩阵不等式成立,
,使得下面的线性矩阵不等式成立,
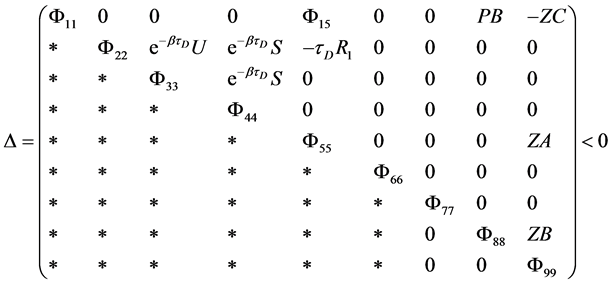 (6)
(6)
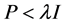
其中
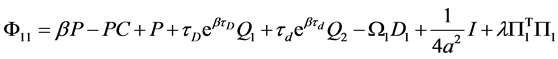
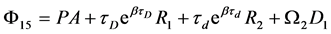

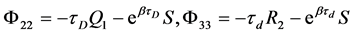

“ ”表示矩阵的对称项,则Hopfield神经网络(1)是随机一致最终有界的。
”表示矩阵的对称项,则Hopfield神经网络(1)是随机一致最终有界的。
证明:考虑下面的Lyapunov-Krasovskii,
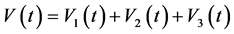 , (7)
, (7)
其中,
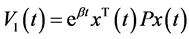 ,
,
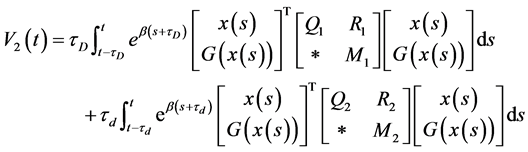
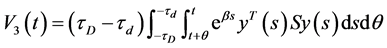 .
.
其中,
我们开始计算 沿系统(1)轨迹的时间导数,得到
沿系统(1)轨迹的时间导数,得到
 (8)
(8)
根据伊藤微分公式,得
 , (9)
, (9)
根据假设2.2,下列不等式成立
 (10)
(10)
结合(9)和(10)式,
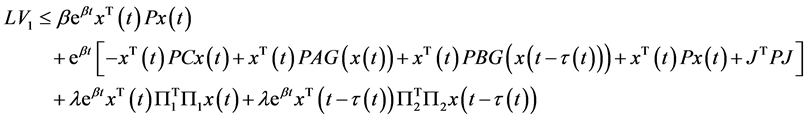 (11)
(11)
另外,
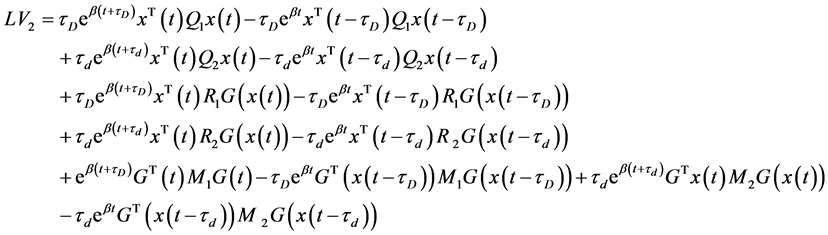 , (12)
, (12)
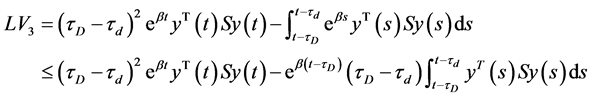 , (13)
, (13)
根据引理2.5,变互式凸组合的方法有较低的保守型,可得到
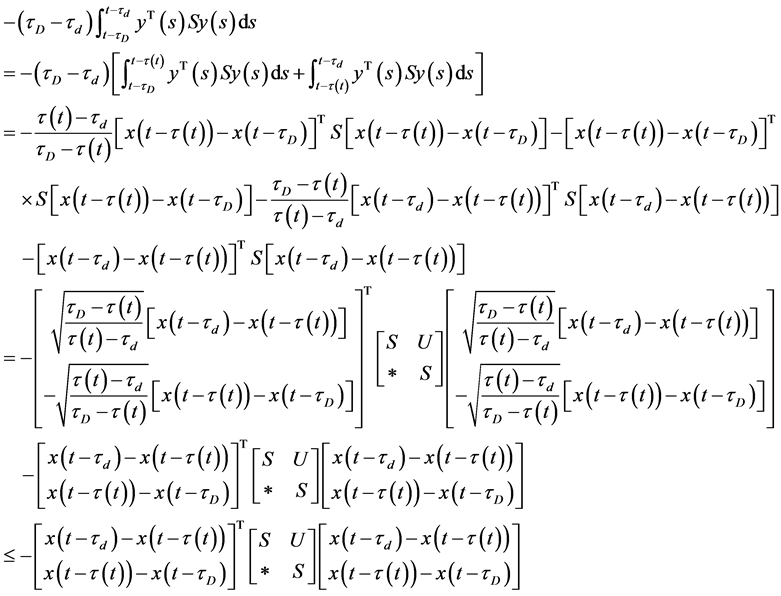 ,(14)
,(14)
即
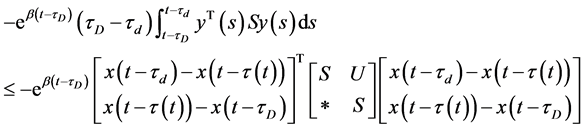 , (15)
, (15)
对任意的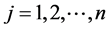 ,根据假设2.1,易得
,根据假设2.1,易得
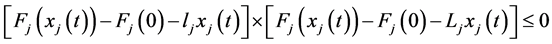 (16)
(16)
和
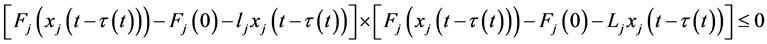 (17)
(17)
从而有
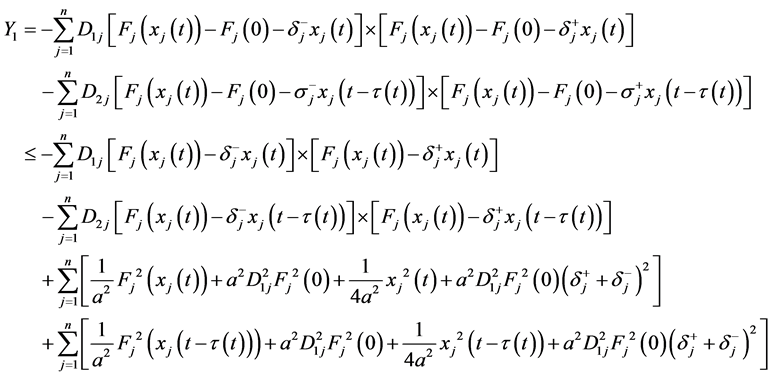 (18)
(18)
对任意的自由权矩阵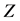 ,得到,
,得到,
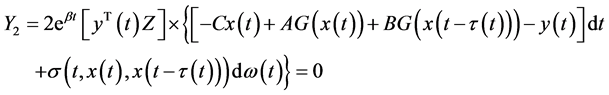 (19)
(19)
定义
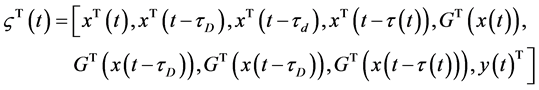
根据(8)~(19),得到
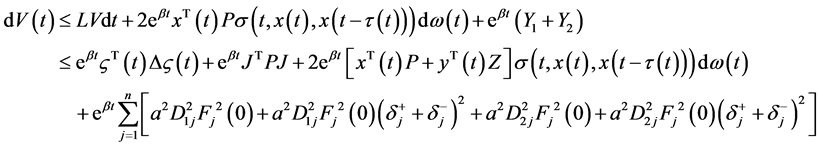 (20)
(20)
令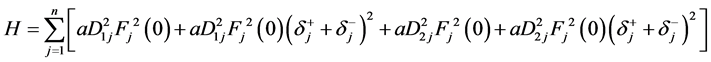
两边同时对不等式(20)从 到
到 积分,并且取期望
积分,并且取期望
 , (21)
, (21)
由(7)式得到
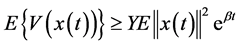 , (22)
, (22)
使得
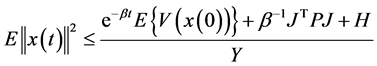 , (23)
, (23)
其中,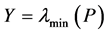 。
。
对任意的常数 和
和 ,有
,有 ,若取
,若取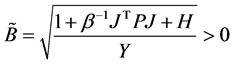 ,对所有的
,对所有的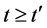 ,使得
,使得 成立。
成立。
根据定义2.3,对所有的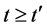 ,使得
,使得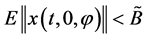 。也就是说,系统(1)是随机一致最终有界的。证毕。
。也就是说,系统(1)是随机一致最终有界的。证毕。
定理2.7:假如定理2.6成立,系统(1)存在一个随机吸引子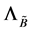 ,使得
,使得 .
.
证明:选取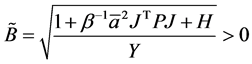 ,定理2.6表明对任意的
,定理2.6表明对任意的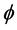 ,有
,有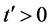 ,当
,当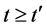 ,使得
,使得
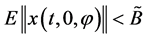 . 让
. 让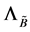 记为
记为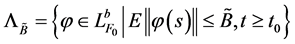 。显然,
。显然,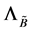 是闭的,有界的,不变的. 从而有
是闭的,有界的,不变的. 从而有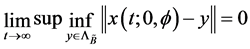 。因此,
。因此,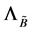 是系统(1)解的一个随机吸引子。证毕。
是系统(1)解的一个随机吸引子。证毕。
定理2.8:如果定理2.6对所有的情况都成立,当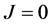 ,
,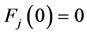 时,系统(1)有一个初始解
时,系统(1)有一个初始解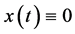 ,使得系统(1)的初始解是均方指数稳定的.
,使得系统(1)的初始解是均方指数稳定的.
证明:当 ,
,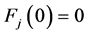 时,显然
时,显然 ,是系统(1)的初始解.
,是系统(1)的初始解.
根据定理2.6,对任意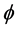 ,我们推得
,我们推得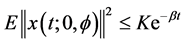 ,其中,
,其中, 。
。
因此,系统(1)的初始解是均方指数稳定的.证毕.
备注2.9:本文主要运用线性矩阵不等式的理论,是一种构造性证明问题,通过构造负定的矩阵不等式(6),利用MATLAB中的LMI工具箱寻找使(6)成立的正定未知矩阵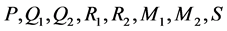 ,从而保证定理2.6的合理性。
,从而保证定理2.6的合理性。
3. 数值模拟
考虑下面随机Hopfield神经网络
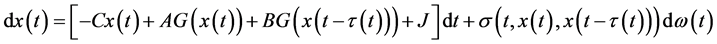 (24)
(24)
参量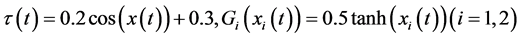 ,连接权矩阵满足
,连接权矩阵满足
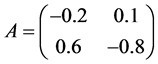 ,
,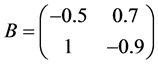 ,
, ,
,
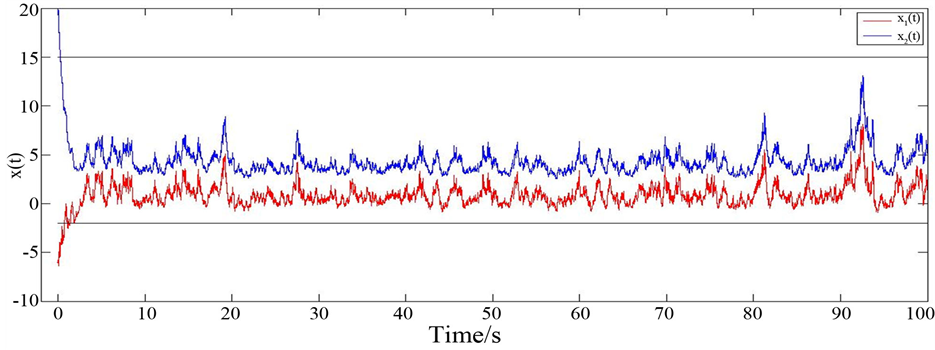
Figure 1. Stochastic uniformly ultimate boundness of system
图1. 系统的随机一致最终有界性
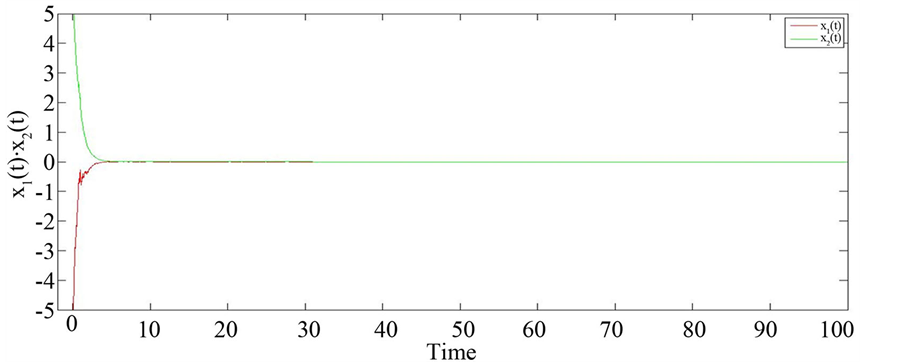
Figure 2. Mean square exponential stability with initial value [-5,5]
图2. 初始值为[-5,5]下的均方指数稳定性
因此,当 ,运用MATLAB中的LMI控制工具箱,计算LMIS,(6)可得到可行解
,运用MATLAB中的LMI控制工具箱,计算LMIS,(6)可得到可行解
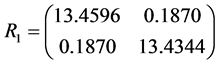
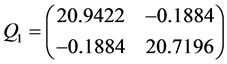
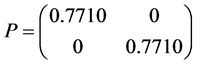
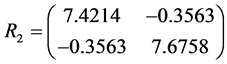
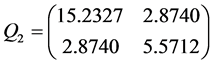
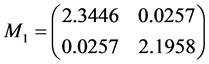
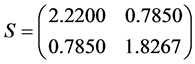
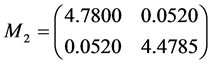 ,
,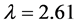
则相应的图像如图1,图2。
致 谢
本文是在导师李友云教授和王鹏同学的悉心指导下完成的,在此论文发表之际向我的导师和帮助我的朋友致以深深地敬意和衷心的感谢。