摘要:
本文主要提出了非线性Sine-Gordon方程的H1-Galerkin非协调混合元方法的全离散逼近格式。利用双线性元和一个非协调元的性质及插值理论,分别得到了原始变量和流量在H1模和H(div,Ω)模下具有O(h2+τ2)阶的超逼近性质。
Abstract: In this paper, an H1-Galerkin nonconforming mixed finite element method is mainly proposed for Sine-Gordon equations under fully-discrete scheme. By use of the properties of bilinear element and a nonconforming element and interpolation theory, the supercloseness properties are derived for the original variable in H1 norm and the flux variable in H(div,Ω) norm with order O(h2+τ2) , respectively.
1. 引言
本文考虑下面Sine-Gordon (SG)方程
 (1)
(1)
其中 为有界矩形区域,
为有界矩形区域, 为
为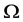 的边界,
的边界, ,
, ,
, 是正常数,
是正常数,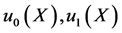 是已知充分光滑的函数。
是已知充分光滑的函数。
SG方程常用于描绘磁性晶体的Bloch壁运动,沿类脂膜的扩张波的传播等。已有很多关于其数值解的研究,[1] [2] 分别研究了半离散格式下的一类非协调元和协调元方法。[3] 借助插值与投影之间的关系给出了线性三角形元半离散和全离散格式下新的高精度分析。 [4] 提出了H1-Galerkin混合元方法,它不要求具备传统混合元方法所要求满足的B-B条件,已被广泛应用于伪双曲线方程 [5] 和双曲线积分微分方程 [6] 等。 [7] 借助投影讨论了(1)中 时的H1-Galerkin混合元方法,给出了最优误差估计式。
时的H1-Galerkin混合元方法,给出了最优误差估计式。
本文主要建立方程(1)的H1-Galerkin非协调混合元方法的全离散逼近格式。首先通过引入流量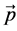 对原始问题进行等价变形,然后分别用双线性元和交叉单元对原始变量和流量进行逼近建立其全离散格式。最后借助这两个单元的性质得到了这两个变量分别在
对原始问题进行等价变形,然后分别用双线性元和交叉单元对原始变量和流量进行逼近建立其全离散格式。最后借助这两个单元的性质得到了这两个变量分别在 模和
模和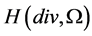 模下的超逼近性质。
模下的超逼近性质。
2. 混合元格式的单元构造及性质
为方便起见,设 是对
是对 的一族矩形剖分。给定
的一族矩形剖分。给定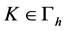 ,边长分别为
,边长分别为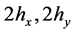 ,与
,与 轴和
轴和 轴平行的边分别为
轴平行的边分别为 和
和 ,四顶点依次记作
,四顶点依次记作 。记
。记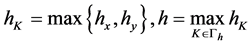 。
。
定义混合元有限元 :
:
 ,
,
 ,
,
 ,
,
其中 ,
,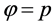 或
或 。
。
相关的有限元空间 和
和 分别定义为
分别定义为
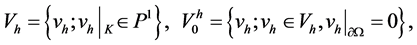

这里 为
为 穿过边界
穿过边界 的跳跃值,且当
的跳跃值,且当 时,
时, 。记
。记 和
和 分别为
分别为 和
和 的插值算子。
的插值算子。
[8] 和 [5] 中已分别证明如下性质。
引理1 设 ,则
,则

引理 2 假定 ,
, ,对
,对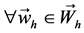 ,成立
,成立

令 ,则方程(1)可变形为
,则方程(1)可变形为
 (2)
(2)
(2)的变分形式为:求 使得
使得
 (3)
(3)
3. 全离散格式的超逼近分析
把时间区间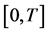 进行
进行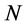 等分,则时间步长
等分,则时间步长 ,时间节点
,时间节点 。对于任意光滑函数
。对于任意光滑函数 ,定义
,定义


全离散逼近格式:求 ,使得
,使得
 (4)
(4)
其中 。
。
令 ,
,
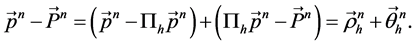
下面我们给出本文的超逼近结果。
定理1 设 分别是(2)和(4)的解。假定
分别是(2)和(4)的解。假定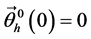 ,
, ,
, ,
, ,
, ,则对任意正整数
,则对任意正整数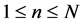 ,有
,有

这里 。
。
证明 对于任意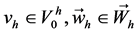 ,由(2)得
,由(2)得
 (5)
(5)
其中 。
。
结合(4)和(5)得如下误差方程
 (6)
(6)
在(6)中取 ,则
,则
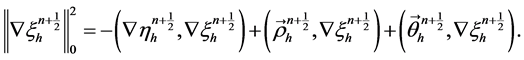
根据引理1得

由Schwartz引理和插值理论得
 ,
,
 .
.
因此
 . (7)
. (7)
在(6)中取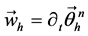 。再添加上项
。再添加上项 ,则
,则

注意到等式左端两项可以变形为
 ,
,
 .
.
下面依次估计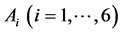 。借助插值理论和Young不等式,我们得
。借助插值理论和Young不等式,我们得
 (8)
(8)
 . (9)
. (9)
利用引理2,我们有
 . (10)
. (10)
对于非线性项 ,先变形再利用函数
,先变形再利用函数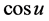 的Lipschtiz连续性得
的Lipschtiz连续性得
 (11)
(11)
显然, 可估计为
可估计为
 (12)
(12)
综合(8)~(12),再消去 得
得

上式两边同乘以 ,然后关于n从1到
,然后关于n从1到 求和,我们得
求和,我们得

根据定义知 ,且
,且 。因此
。因此
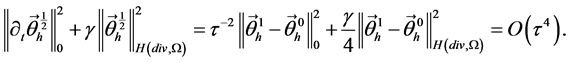
又

利用Young不等式得

类似地,
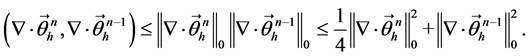
因此选取适当的 满足
满足 ,我们得
,我们得

其中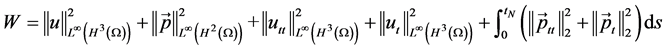 .
.
再利用离散的Gronwall不等式,可导出
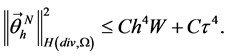 (13)
(13)
再结合(7)及(13)式,我们有
 .
.
定理1得证。
基金项目
许昌学院青年骨干教师项目。